Função contínua

Parte da série sobre
Matemática
História
Áreas Teoria dos números Geometria Álgebra Cálculo e Análise Matemática discreta Lógica matemática e Teoria dos conjuntos Probabilidade Estatística e Teoria da decisão Relação com as ciências Física Química Computação Biologia Linguística Economia Filosofia Educação
Portal da Matemática

Em matemática, uma função é contínua quando, intuitivamente, as pequenas variações nos objectos correspondem a pequenas variações nas imagens. Nos pontos onde a função não é contínua, diz-se que a função é descontínua, ou que se trata de um ponto de descontinuidade.

Definições de Continuidade

Em espaço topológico

Diz-se que uma função $f:X\rightarrow Y$ entre espaços topológicos é contínua se a imagem recíproca de qualquer aberto de $Y$ é um aberto de $X$. Em termos de bolas, Dados dois espaços topológicos $M,N$ dizemos que a aplicação $f:M\longrightarrow N$ é contínua em $a\in M$ da seguinte forma: Tomando as bolas abertas $B'=B(f(a),\epsilon )$ e $B=B(a,\delta )$, tem-se que $f(B)\subset B'$,com $\epsilon >0$ e $\delta >0$.

Exemplos

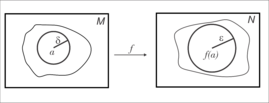
Esta função é descontínua nos inteiros.

Estes exemplos usam propriedades da imagem recíproca, ou seja, dada uma função $f:X\rightarrow Y$ e um conjunto $A\subset Y$, o conjunto $f^{-1}(A)=\{x\in X|f(x)\in A\}$.

• Seja $X$ um conjunto com a topologia discreta $\tau _{X}=P(X)$, $Y$ com qualquer topologia, então qualquer função $f:X\rightarrow Y$ é contínua.

Basta ver que, $\forall A\in Y$ aberto temos que, $f^{-1}(A)\in P(X)$, e portanto é aberto, o que mostra que $f$ é uma função contínua.

• Seja $Y$ um conjunto com a topologia grosseira $\tau _{Y}=\{\varnothing ,Y\}$, $X$ com qualquer topologia, então qualquer função $f:X\rightarrow Y$ é contínua.

De fato, pois, como os dois únicos abertos de $\tau _{Y}$ são $\varnothing$ e $Y$, basta verificar se suas imagens inversas são abertos. Mas $f^{-1}(\varnothing )=\varnothing$ e $f^{-1}(Y)=X$, e, por definição, $\varnothing$ e $X$ são abertos em qualquer topologia em $X$.

• Sejam $f:X\rightarrow Y$ e $g:Y\rightarrow Z$ funções contínuas. Então $g\circ f:X\rightarrow Z$ também é uma função contínua.

Fato pois: qualquer que seja $A\subset Z$ aberto, pela continuidade de $g$, temos que $g^{-1}(A)$ é um aberto em $Y$. Portanto, pela continuidade de $f$, $f^{-1}(g^{-1}(A))$ é um aberto em $X$. Mas $f^{-1}(g^{-1}(A))=(g\circ f)^{-1}(A)$, o que prova a continuidade de $g\circ f$.

• Seja $f:X\longrightarrow Y$ , $X$ e $Y$ espaços métricos não vazios. Se $\forall x,y\in X$ tivermos que $d(f(x),f(y))\leq c\cdot d(x,y)$, então a aplicação $f$ é contínua e a constante $c$ é chamada de constante de Lipschitz. Na reta Real toda aplicação Lipschitiziana é uniformemente contínua.

Em espaço métrico

Diz-se que uma função $f$ é contínua no ponto $x=a$ se $a$ é um ponto isolado do domínio ou, caso seja ponto de acumulação de $X$, se existir o limite de $f(x)$ com $x$ tendendo a $a$ e esse limite for igual a $f(a)$.

OBS.:Não faz sentido calcular limites em pontos que não são de acumulação. Caso insistíssemos teríamos que qualquer valor seria limite de $f(x)$ com $x$ tendendo a $a$

Em análise real, essa definição é escrita na forma tradicional Epsilon-Delta, ou seja, diz-se que uma função $f$ é contínua num ponto $a$ do seu domínio se,

dado $\epsilon >0,\exists \delta >0$ tal que $\forall x\in X,a-\delta <x<a+\delta$ então .$f(a)-\epsilon <f(x)<f(a)+\epsilon$

Esta definição, com uma pequena adaptação, pode ser usada para uma função de um espaço métrico $E$ em outro espaço métrico $F$: a função $f$ é contínua em $a\in E$ quando

dado $\epsilon >0,\exists \delta >0$ tal que $\forall x\in E,d_{E}(x,a)<\delta \rightarrow d_{F}(f(x),f(a))<\epsilon$.

Diz-se que f é contínua em seu domínio, ou simplesmente contínua, se ela for contínua em todos os pontos desse domínio.

Equivalência das Definições

Se $E$ e $F$ são espaços métricos, e $\tau _{E}{\mbox{ e }}\tau _{F}$ as topologias geradas pelas métricas em $E$ e $F$, então uma função $f:E\rightarrow F$ é contínua pela definição topológica se, e somente se, ela é contínua pela definição métrica.

Em termos de limites

Uma função $f(x)$ é dita ser contínua em um ponto $a$ de seu domínio se:

$\lim _{x\to a}f(x)=f(a)$

Observa-se que esta definição exige que o limite à esquerda exista assim como o limite da direita e que a função esteja definida no ponto com o mesmo valor de limite para o ponto.

Função Sequencialmente Contínua

Uma função $f:E\rightarrow F$, em que $E$ e $F$ são espaços topológicos, é sequencialmente contínua em um ponto $a\in E$ quanto ela comuta com o limite de sequências, ou seja, quando para toda sequência $x_{i}\in E$ cujo limite (em $E$) seja $a$, temos que o limite (em $F$) de $f(x_{i})$ é $f(a)$. Uma forma elegante de escrever isso é $\lim _{i\rightarrow \infty }f(x_{i})=f(\lim _{i\rightarrow \infty }x_{i})$.

Propriedades

• Função Composta: Se $f:E\to F$ e $g:F\to G$ são funções contínuas, então é imediato (pela definição topológica) que a função composta $g\circ f:E\to G$ é contínua.
• Se $f:X\rightarrow Y$ é uma bijeção contínua de um espaço topológico compacto $X$ em um espaço topológico de Hausdorff $Y$, então $f$ é um homeomorfismo.
• O conjunto dos zeros de uma aplicação contínua entre um espaço topológico $X$ e a reta real $\mathbb {R}$, com a topologia usual, é um conjunto fechado. Em particular, o conjunto das matrizes singulares é fechado em $\mathbb {R} ^{n\times n}$, pois o determinante define uma aplicação contínua nesse espaço.
• Sejam $X$ e $Y$ dois espaços topológicos, $U\subset X$ e $f:X\rightarrow Y$ uma aplicação contínua. Então $f$ restrita a $U$ ainda é uma aplicação contínua.

  Referências

  • Munkres, J. (1966). Elementary Differential Topology, edição revisada. Col: Annals of Mathematics Studies 54. [S.l.]: Princeton University Press. ISBN 0-691-09093-9 
  • Lima, Elon Lages (2013). Análise Real - Funções de uma variável. Col: Coleção Matemática Universitária. 1 12ª ed. [S.l.]: IMPA. 198 páginas. ISBN 978-85-244-0048-3