Os números inteiros são constituídos dos números naturais e seus simétricos negativos, podendo ou não incluir o zero. O conjunto de todos os números inteiros é representado pela letra
Z
{\displaystyle \mathbb {Z} }
Zahl ).
Z
=
[
.
.
.
−
3
,
−
2
,
−
1
,
1
,
2
,
3...
]
{\displaystyle \mathbb {Z} =[...-3,-2,-1,1,2,3...]}
Subconjuntos de
Z
{\displaystyle \mathbb {Z} }
[ editar | editar código-fonte ]
Z
∗
=
{\displaystyle \mathbb {Z} ^{*}=}
=
Z
−
[
0
]
{\displaystyle =\mathbb {Z} -[0]}
Z
{\displaystyle \mathbb {Z} }
+
=
{\displaystyle =}
=
[
0
,
1
,
2
,
3...
]
{\displaystyle =[0,1,2,3...]}
Z
∗
{\displaystyle \mathbb {Z} ^{*}}
+
=
{\displaystyle =}
=
[
1
,
2
,
3...
]
{\displaystyle =[1,2,3...]}
Z
{\displaystyle \mathbb {Z} }
-
=
{\displaystyle =}
=
[
.
.
.
−
3
,
−
2
,
−
1
,
0
]
{\displaystyle =[...-3,-2,-1,0]}
Z
∗
{\displaystyle \mathbb {Z} ^{*}}
-
=
{\displaystyle =}
=
[
.
.
.
−
3
,
−
2
,
−
1
]
{\displaystyle =[...-3,-2,-1]}
Propriedades Básicas das operações
+
{\displaystyle +}
⋅
{\displaystyle \cdot }
[ 1] [ editar | editar código-fonte ] Há diversos campos numéricos verificando as propriedades abaixo. Dizemos que eles têm uma mesma estrutura algébrica, a qual é chamada de anel de integridade . O campo dos inteiros,
[
Z
,
+
,
⋅
]
{\displaystyle [\mathbb {Z} ,+,\cdot ]}
Para todos
a
,
b
,
c
∈
Z
{\displaystyle a,b,c\in \mathbb {Z} }
a
+
b
∈
Z
{\displaystyle a+b\in \mathbb {Z} }
{\displaystyle \qquad }
+
{\displaystyle +}
a
⋅
b
∈
Z
{\displaystyle a\cdot b\in \mathbb {Z} }
{\displaystyle \qquad \qquad }
⋅
{\displaystyle \cdot }
a
+
(
b
+
c
)
=
(
a
+
b
)
+
c
{\displaystyle a+(b+c)=(a+b)+c}
{\displaystyle \qquad \qquad }
+
{\displaystyle +}
a
⋅
(
b
⋅
c
)
=
(
a
⋅
b
)
⋅
c
{\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c}
{\displaystyle \qquad \qquad }
⋅
{\displaystyle \cdot }
a
+
0
=
a
{\displaystyle a+0=a}
{\displaystyle \qquad \qquad }
+
{\displaystyle +}
a
⋅
1
=
a
{\displaystyle a\cdot 1=a}
{\displaystyle \qquad \qquad }
⋅
{\displaystyle \cdot }
a
+
b
=
b
+
a
{\displaystyle a+b=b+a}
{\displaystyle \qquad \qquad }
+
{\displaystyle +}
a
⋅
b
=
b
⋅
a
{\displaystyle a\cdot b=b\cdot a}
{\displaystyle \qquad \qquad }
⋅
{\displaystyle \cdot }
∃
a
′
∈
Z
{\displaystyle \exists a'\in \mathbb {Z} }
a
+
a
′
=
0
{\displaystyle a+a'=0}
{\displaystyle \qquad \qquad }
a
′
{\displaystyle a'}
a
{\displaystyle a}
a
⋅
(
b
+
c
)
=
(
a
⋅
b
)
+
(
a
⋅
c
)
{\displaystyle a\cdot (b+c)=(a\cdot b)+(a\cdot c)}
{\displaystyle \qquad \qquad }
⋅
{\displaystyle \cdot }
a
⋅
b
=
0
⇒
{\displaystyle a\cdot b=0\Rightarrow }
a
=
0
{\displaystyle a=0}
b
=
0
{\displaystyle b=0}
{\displaystyle \qquad \qquad }
⋅
{\displaystyle \cdot }
i
)
{\displaystyle i)}
Unicidade do elemento neutro da multiplicação
Vamos supor por absurdo que existem dois elementos neutros da multiplicação
1
{\displaystyle 1}
1
′
{\displaystyle 1'}
1
≠
1
′
{\displaystyle 1\neq 1'}
Como
1
{\displaystyle 1}
1
′
⋅
1
=
1
′
{\displaystyle 1'\cdot 1=1'}
Como
1
′
{\displaystyle 1'}
1
⋅
1
′
=
1
{\displaystyle 1\cdot 1'=1}
Temos:
1
′
=
1
′
⋅
1
=
1
⋅
1
′
=
1
{\displaystyle 1'=1'\cdot 1=1\cdot 1'=1}
⇒
1
′
=
1
{\displaystyle \qquad \quad \Rightarrow 1'=1}
Pois
1
′
{\displaystyle 1'}
1
{\displaystyle 1}
Então o elemento neutro da multiplicação é único.
i
i
)
{\displaystyle ii)}
Unicidade do elemento simétrico
Vamos supor que existem dois simétricos
a
′
{\displaystyle a'}
a
″
{\displaystyle a''}
a
{\displaystyle a}
a
′
≠
a
″
{\displaystyle a'\neq a''}
a
′
=
0
+
a
′
{\displaystyle a'=0+a'}
=
(
a
+
a
″
)
+
a
′
{\displaystyle \quad =(a+a'')+a'}
=
a
+
(
a
″
+
a
′
)
{\displaystyle \quad =a+(a''+a')}
=
a
+
(
a
′
+
a
″
)
{\displaystyle \quad =a+(a'+a'')}
=
(
a
+
a
′
)
+
a
″
{\displaystyle \quad =(a+a')+a''}
=
0
+
a
″
=
a
″
{\displaystyle \quad =0+a''=a''}
Notação para o simétrico de
a
{\displaystyle a}
−
a
{\displaystyle -a}
Como por hipótese
a
′
≠
a
″
{\displaystyle a'\neq a''}
a
′
=
a
″
{\displaystyle a'=a''}
Logo o simétrico da adição é único.
Com isso podemos definir a subtração:
a
+
b
′
=
a
+
(
−
b
)
=
a
−
b
{\displaystyle \qquad a+b'=a+(-b)=a-b}
i
i
i
)
{\displaystyle iii)}
Multiplicação por
0
{\displaystyle 0}
0
⋅
a
=
0
{\displaystyle \qquad 0\cdot a=0}
∀
a
∈
Z
{\displaystyle \forall a\in \mathbb {Z} }
⇒
0
⋅
a
=
(
b
−
b
)
a
{\displaystyle \qquad \Rightarrow 0\cdot a=(b-b)a}
⇒
0
⋅
a
=
a
b
−
a
b
{\displaystyle \qquad \Rightarrow 0\cdot a=ab-ab}
⇒
0
⋅
a
=
0
{\displaystyle \qquad \Rightarrow 0\cdot a=0}
i
v
)
{\displaystyle iv)}
Distributividade
(
b
+
c
)
a
=
b
a
+
c
a
{\displaystyle (b+c)a=ba+ca}
(
b
+
c
)
a
=
a
(
b
+
c
)
{\displaystyle (b+c)a=a(b+c)}
⇒
a
b
+
a
c
=
b
a
+
c
a
{\displaystyle \Rightarrow ab+ac=ba+ca}
i
)
{\displaystyle i)}
a
{\displaystyle a}
b
{\displaystyle b}
a
+
c
=
b
+
c
⇒
a
=
b
,
{\displaystyle \qquad a+c=b+c\Rightarrow a=b,}
∀
c
∈
Z
{\displaystyle \forall c\in \mathbb {Z} }
Observe que, para
x
=
y
,
{\displaystyle x=y,}
x
,
y
∈
Z
{\displaystyle \quad x,y\in \mathbb {Z} }
z
∈
Z
{\displaystyle z\in \mathbb {Z} }
Logo temos,
x
+
z
=
y
+
z
{\displaystyle x+z=y+z}
N
{\displaystyle \mathbb {N} }
Agora podemos provar:
a
+
c
=
b
+
c
{\displaystyle \qquad a+c=b+c}
⇒
(
a
+
c
)
+
(
−
c
)
=
(
b
+
c
)
+
(
−
c
)
{\displaystyle \qquad \Rightarrow (a+c)+(-c)=(b+c)+(-c)}
⇒
a
+
(
c
−
c
)
=
b
+
(
c
−
c
)
{\displaystyle \qquad \Rightarrow a+(c-c)=b+(c-c)}
⇒
a
+
0
=
b
+
0
{\displaystyle \qquad \Rightarrow a+0=b+0}
⇒
a
=
b
{\displaystyle \qquad \Rightarrow a=b}
i
i
)
{\displaystyle ii)}
a
,
b
{\displaystyle a,b}
c
{\displaystyle c}
a
⋅
c
=
b
⋅
c
⇒
a
=
b
,
{\displaystyle \qquad a\cdot c=b\cdot c\Rightarrow a=b,}
∀
c
≠
0
{\displaystyle \forall c\neq 0}
⇒
a
c
−
b
c
=
b
c
−
b
c
{\displaystyle \qquad \Rightarrow ac-bc=bc-bc}
⇒
c
a
−
c
b
=
0
{\displaystyle \qquad \Rightarrow ca-cb=0}
⇒
c
(
a
−
b
)
=
0
{\displaystyle \qquad \Rightarrow c(a-b)=0}
Logo
c
=
0
{\displaystyle c=0}
a
−
b
=
0
{\displaystyle a-b=0}
c
≠
0
{\displaystyle c\neq 0}
a
−
b
=
0
{\displaystyle \qquad a-b=0}
⇒
a
−
b
+
b
=
0
+
b
{\displaystyle \qquad \Rightarrow a-b+b=0+b}
a
+
0
=
0
+
b
{\displaystyle \qquad a+0=0+b}
a
=
b
{\displaystyle \qquad a=b}
Temos que se
a
>
b
{\displaystyle a>b}
b
<
a
{\displaystyle b<a}
a
−
b
>
0
{\displaystyle a-b>0}
Com isso os números inteiros ficam divididos em:
Z
+
=
{
0
,
1
,
2
,
3...
}
⇒
{\displaystyle \mathbb {Z} ^{+}=\{0,1,2,3...\}\Rightarrow }
Inteiros não negativos
x
∈
Z
:
x
≥
0
{\displaystyle \qquad x\in \mathbb {Z} :x\geq 0}
Z
−
=
{
.
.
.
,
−
3
,
−
2
,
−
1
,
0
}
⇒
{\displaystyle \mathbb {Z} ^{-}=\{...,-3,-2,-1,0\}\Rightarrow }
Inteiros não positivos
x
∈
Z
:
x
≤
0
{\displaystyle \qquad x\in \mathbb {Z} :x\leq 0}
Z
∗
+
=
{
1
,
2
,
3
,
.
.
.
}
⇒
{\displaystyle \mathbb {Z} _{*}^{+}=\{1,2,3,...\}\Rightarrow }
Inteiros positivos
x
∈
Z
:
x
>
0
{\displaystyle \qquad x\in \mathbb {Z} :x>0}
Z
∗
−
=
{
.
.
.
,
−
3
,
−
2
,
−
1
}
⇒
{\displaystyle \mathbb {Z} _{*}^{-}=\{...,-3,-2,-1\}\Rightarrow }
Inteiros negativos
x
∈
Z
:
x
<
0
{\displaystyle \qquad x\in \mathbb {Z} :x<0}
Observação: temos
a
>
b
⇒
a
−
b
>
0
,
{\displaystyle a>b\Rightarrow a-b>0,}
a
−
0
=
a
{\displaystyle a-0=a}
a
>
0
{\displaystyle a>0}
a
∈
{
1
,
2
,
3
,
.
.
.
}
{\displaystyle a\in \{1,2,3,...\}}
Notação:
{
a
≥
b
(
a
>
b
o
u
a
=
b
)
a
≤
b
(
a
<
b
o
u
a
=
b
)
{\displaystyle {\begin{cases}a\geq b(a>b\quad ou\quad a=b)\\a\leq b(a<b\quad ou\quad a=b)\\\end{cases}}}
As relações
<
{\displaystyle <}
≤
{\displaystyle \leq }
Proposição:
Sendo
a
,
b
,
c
∈
Z
{\displaystyle a,b,c\in \mathbb {Z} }
i
)
{\displaystyle i)}
∗
a
<
b
⇔
a
+
c
<
b
+
c
,
∀
c
∈
Z
{\displaystyle *\quad a<b\Leftrightarrow a+c<b+c,\quad \forall c\in \mathbb {Z} }
a
<
b
⇒
b
−
a
>
0
{\displaystyle a<b\Rightarrow b-a>0}
⇒
b
−
a
+
c
−
c
>
0
{\displaystyle \qquad \Rightarrow b-a+c-c>0}
⇒
b
+
c
−
a
−
c
>
0
{\displaystyle \qquad \Rightarrow b+c-a-c>0}
⇒
(
b
+
c
)
−
(
a
+
c
)
>
0
{\displaystyle \qquad \Rightarrow (b+c)-(a+c)>0}
⇒
a
+
c
<
b
+
c
{\displaystyle \qquad \Rightarrow a+c<b+c}
a
+
c
<
b
+
c
⇒
a
<
b
{\displaystyle a+c<b+c\Rightarrow a<b}
⇒
(
b
+
c
)
−
(
a
+
c
)
>
0
{\displaystyle \qquad \qquad \quad \Rightarrow (b+c)-(a+c)>0}
⇒
b
+
c
−
a
−
c
>
0
{\displaystyle \qquad \qquad \quad \Rightarrow b+c-a-c>0}
⇒
(
b
−
a
)
+
(
c
−
c
)
>
0
{\displaystyle \qquad \qquad \quad \Rightarrow (b-a)+(c-c)>0}
⇒
b
−
a
>
0
{\displaystyle \qquad \qquad \quad \Rightarrow b-a>0}
⇒
a
<
b
{\displaystyle \qquad \qquad \quad \Rightarrow a<b}
∗
a
≤
b
⇔
a
+
c
≤
b
+
c
,
∀
c
∈
Z
{\displaystyle *\quad a\leq b\Leftrightarrow a+c\leq b+c,\quad \forall c\in \mathbb {Z} }
Esta demonstração é de forma análoga à anterior.
i
i
)
{\displaystyle ii)}
∗
a
<
b
⇔
a
⋅
c
<
b
⋅
c
,
∀
c
∈
Z
{\displaystyle *\quad a<b\Leftrightarrow a\cdot c<b\cdot c,\quad \forall c\in \mathbb {Z} }
Observe que quando
n
>
0
{\displaystyle n>0}
3
n
>
2
n
>
n
>
0
{\displaystyle 3n>2n>n>0}
c
n
>
0
{\displaystyle cn>0}
c
>
0
{\displaystyle c>0}
a
<
b
⇒
b
−
a
>
0
{\displaystyle a<b\Rightarrow b-a>0}
⇒
c
(
b
−
a
)
>
0
c
>
0
{\displaystyle \qquad \Rightarrow c(b-a)>0\quad \qquad c>0}
⇒
c
b
−
c
a
>
0
{\displaystyle \qquad \Rightarrow cb-ca>0}
⇒
c
a
<
c
b
{\displaystyle \qquad \Rightarrow ca<cb}
c
a
<
c
b
⇒
a
<
b
{\displaystyle ca<cb\Rightarrow a<b}
⇒
c
a
−
c
b
>
0
{\displaystyle \qquad \quad \Rightarrow ca-cb>0}
⇒
c
(
b
−
a
)
>
0
c
>
0
{\displaystyle \qquad \quad \Rightarrow c(b-a)>0\quad \qquad c>0}
⇒
b
−
a
>
0
{\displaystyle \qquad \quad \Rightarrow b-a>0}
⇒
a
<
b
{\displaystyle \qquad \quad \Rightarrow a<b}
Observe que quando
n
>
0
{\displaystyle n>0}
−
3
n
<
−
2
n
<
−
n
<
0
{\displaystyle -3n<-2n<-n<0}
c
n
<
0
{\displaystyle cn<0}
c
<
0
{\displaystyle c<0}
a
<
b
⇒
b
−
a
>
0
{\displaystyle a<b\Rightarrow b-a>0}
⇒
c
(
b
−
a
)
<
0
c
<
0
{\displaystyle \qquad \Rightarrow c(b-a)<0\quad \qquad c<0}
⇒
c
b
−
c
a
<
0
{\displaystyle \qquad \Rightarrow cb-ca<0}
⇒
c
b
<
c
a
{\displaystyle \qquad \Rightarrow cb<ca}
a
<
b
⇒
c
a
>
c
b
{\displaystyle a<b\Rightarrow ca>cb}
⇒
c
b
−
c
a
<
0
{\displaystyle \qquad \Rightarrow cb-ca<0}
⇒
c
(
b
−
a
)
<
0
c
<
0
{\displaystyle \qquad \Rightarrow c(b-a)<0\quad \qquad c<0}
⇒
b
−
a
>
0
{\displaystyle \qquad \Rightarrow b-a>0}
⇒
a
<
b
{\displaystyle \qquad \Rightarrow a<b}
O valor absoluto de um número inteiro
b
{\displaystyle b}
|
b
|
=
{
b
s
e
b
≥
0
−
b
s
e
b
<
0
{\displaystyle |b|={\begin{cases}b\ se\ b\geq 0\\-b\ se\ b<0\\\end{cases}}}
Tomar o valor absoluto de um número inteiro consiste basicamente em deixá-lo inalterado se o número for positivo ou nulo, e apagar seu sinal, caso ele seja negativo.
Exemplo:
|
−
2
|
=
2
=
|
2
|
{\displaystyle |-2|=2=|2|}
|
0
|
=
0
{\displaystyle |0|=0}
O divisor de um número inteiro
a
{\displaystyle a}
b
{\displaystyle b}
a
{\displaystyle a}
a
=
b
.
c
{\displaystyle a=b.c}
c
{\displaystyle c}
Sempre que
b
{\displaystyle b}
a
{\displaystyle a}
{\displaystyle \qquad }
b
{\displaystyle b}
a
{\displaystyle a}
b
|
a
{\displaystyle b|a}
{\displaystyle \qquad }
a
{\displaystyle a}
b
{\displaystyle b}
Exemplo:
Os divisores de
a
=
4
{\displaystyle a=4}
b
=
−
2
,
−
1
,
1
,
2
{\displaystyle b=-2,-1,1,2}
Todos eles são não-nulos, e temos respectivamente:
4
=
(
−
2
)
⋅
(
−
2
)
,
4
=
(
−
1
)
⋅
(
−
4
)
,
4
=
1
⋅
4
,
4
=
2
⋅
2
{\displaystyle 4=(-2)\cdot (-2),\quad 4=(-1)\cdot (-4),\quad 4=1\cdot 4,\quad 4=2\cdot 2}
Atenção:
zero só é divisor dele mesmo;
todos os inteiros são divisores de zero.
i
)
{\displaystyle i)}
b
{\displaystyle b}
a
{\displaystyle a}
−
b
{\displaystyle -b}
Hipótese:
b
∣
a
⇒
a
=
b
⋅
c
c
∈
Z
{\displaystyle b\mid a\Rightarrow a=b\cdot c\qquad c\in \mathbb {Z} }
Tese:
−
b
∣
a
⇒
a
=
−
b
⋅
d
d
∈
Z
{\displaystyle -b\mid a\Rightarrow a=-b\cdot d\qquad d\in \mathbb {Z} }
Temos que
a
=
b
⋅
c
{\displaystyle a=b\cdot c}
Então
(
−
1
)
a
=
b
⋅
c
(
−
1
)
{\displaystyle (-1)a=b\cdot c(-1)}
⇒
(
−
1
)
−
a
=
(
−
1
)
b
⋅
(
−
c
)
{\displaystyle \Rightarrow (-1)-a=(-1)b\cdot (-c)}
⇒
a
=
(
−
b
)
⋅
(
−
c
)
{\displaystyle \Rightarrow a=(-b)\cdot (-c)}
d
=
−
c
{\displaystyle d=-c}
⇒
a
=
−
b
.
d
{\displaystyle \Rightarrow a=-b.d}
⇒
−
b
∣
a
{\displaystyle \Rightarrow -b\mid a}
i
i
)
{\displaystyle ii)}
a
{\displaystyle a}
b
{\displaystyle b}
b
{\displaystyle b}
a
{\displaystyle a}
a
=
b
{\displaystyle a=b}
Hipótese:
a
∣
b
{\displaystyle a\mid b}
b
∣
a
{\displaystyle b\mid a}
Tese:
a
=
b
{\displaystyle a=b}
Temos que
a
∣
b
⇒
b
=
a
⋅
c
{\displaystyle a\mid b\Rightarrow b=a\cdot c}
c
∈
Z
{\displaystyle \qquad c\in \mathbb {Z} }
b
∣
a
⇒
a
=
b
⋅
d
{\displaystyle \qquad \qquad b\mid a\Rightarrow a=b\cdot d}
d
∈
Z
{\displaystyle \qquad d\in \mathbb {Z} }
⇒
b
=
(
b
⋅
d
)
⋅
c
⇒
d
⋅
c
=
1
{\displaystyle \Rightarrow b=(b\cdot d)\cdot c\Rightarrow d\cdot c=1}
⇒
d
=
c
=
1
{\displaystyle \Rightarrow d=c=1}
d
=
c
=
−
1
{\displaystyle d=c=-1}
Para
d
=
c
=
1
{\displaystyle d=c=1}
a
=
b
⋅
d
⇒
a
=
b
⋅
1
⇒
a
=
b
{\displaystyle a=b\cdot d\Rightarrow a=b\cdot 1\Rightarrow a=b}
b
=
a
.
c
⇒
b
=
a
⋅
1
⇒
b
=
a
{\displaystyle b=a.c\Rightarrow b=a\cdot 1\Rightarrow b=a}
Para
d
=
c
=
−
1
{\displaystyle d=c=-1}
a
=
b
⋅
d
⇒
a
=
b
⋅
(
−
1
)
⇒
a
=
−
b
{\displaystyle a=b\cdot d\Rightarrow a=b\cdot (-1)\Rightarrow a=-b}
b
=
a
.
c
⇒
b
=
a
⋅
(
−
1
)
⇒
b
=
−
a
{\displaystyle b=a.c\Rightarrow b=a\cdot (-1)\Rightarrow b=-a}
⇒
b
=
−
(
−
b
)
{\displaystyle \Rightarrow b=-(-b)}
⇒
b
=
b
{\displaystyle \Rightarrow b=b}
Como
1
,
−
1
,
a
,
−
a
{\displaystyle 1,-1,a,-a}
a
≠
0
{\displaystyle a\neq 0}
divisores triviais, ou os divisores impróprios, de
a
{\displaystyle a}
Nos casos em que
a
=
1
{\displaystyle a=1}
a
=
−
1
{\displaystyle a=-1}
a
≠
0
{\displaystyle a\neq 0}
Número primo é todo inteiro
p
≠
0
,
±
1
{\displaystyle p\neq 0,\pm 1}
p
{\displaystyle p}
p
,
−
p
,
1
,
−
1
{\displaystyle p,-p,1,-1}
Número composto é todo inteiro
k
≠
0
{\displaystyle k\neq 0}
k
≠
0
{\displaystyle k\neq 0}
Chamamos de divisor comum de dois ou mais números inteiros, todo inteiro que seja divisor de cada um desses inteiros.
Exemplo:
Os divisores de
8
{\displaystyle 8}
±
1
,
±
2
,
±
4
,
±
8
{\displaystyle \pm 1,\pm 2,\pm 4,\pm 8}
12
{\displaystyle 12}
±
1
,
±
2
,
±
3
,
±
4
,
±
6
,
±
12
{\displaystyle \pm 1,\pm 2,\pm 3,\pm 4,\pm 6,\pm 12}
8
{\displaystyle 8}
12
{\displaystyle 12}
±
1
,
±
2
,
±
4
{\displaystyle \pm 1,\pm 2,\pm 4}
Dizemos que dois números inteiros são relativamente primos, ou primos entre si se tiverem como divisores comuns apenas os divisores triviais
+
1
{\displaystyle +1}
−
1
{\displaystyle -1}
Proposição: todo número primo que não dividir um inteiro
a
{\displaystyle a}
a
{\displaystyle a}
p
{\displaystyle p}
a
{\displaystyle a}
p
{\displaystyle p}
1
{\displaystyle 1}
−
1
{\displaystyle -1}
p
{\displaystyle p}
−
p
{\displaystyle -p}
p
{\displaystyle p}
a
{\displaystyle a}
1
{\displaystyle 1}
−
1
{\displaystyle -1}
Chamamos de máximo divisor comum de dois ou mais números inteiros, o maior dos divisores comuns desses inteiros. A notação
m
d
c
(
a
,
b
)
{\displaystyle mdc(a,b)}
a
{\displaystyle a}
b
{\displaystyle b}
Exemplo:
Temos
m
d
c
(
6
,
9
)
=
3
{\displaystyle mdc(6,9)=3}
6
{\displaystyle 6}
9
{\displaystyle 9}
±
1
{\displaystyle \pm 1}
±
3
{\displaystyle \pm 3}
Note que:
o
m
d
c
(
a
,
b
)
{\displaystyle mdc(a,b)}
a
=
b
=
0
{\displaystyle a=b=0}
m
d
c
(
0
,
b
)
=
{
(
b
)
,
s
e
b
≠
0
∄
s
e
b
=
0
}
{\displaystyle mdc(0,b)={\begin{Bmatrix}(b),se\quad b\neq 0\\\nexists \quad se\quad b=0\end{Bmatrix}}}
o conjunto de divisores comuns de qualquer conjunto de dois ou mais números inteiros nunca é vazio (pois
±
1
{\displaystyle \pm 1}
c
≠
0
{\displaystyle c\neq 0}
c
{\displaystyle c}
−
c
{\displaystyle -c}
o
m
d
c
(
a
,
b
)
≥
1
{\displaystyle mdc(a,b)\geq 1}
m
d
c
(
a
,
b
)
=
m
d
c
(
−
a
,
b
)
=
m
d
c
(
a
,
−
b
)
=
m
d
c
(
−
a
,
−
b
)
{\displaystyle mdc(a,b)=mdc(-a,b)=mdc(a,-b)=mdc(-a,-b)}
Dizer que dois números
a
{\displaystyle a}
b
{\displaystyle b}
m
d
c
(
a
,
b
)
=
1
{\displaystyle mdc(a,b)=1}
→
{\displaystyle \rightarrow }
Fatoração: sendo
a
=
b
1
,
b
2
.
.
.
b
n
{\displaystyle a=b_{1},b_{2}...b_{n}}
a
,
b
1
,
b
2
.
.
.
b
n
{\displaystyle a,b_{1},b_{2}...b_{n}}
b
1
,
b
2
.
.
.
b
n
{\displaystyle b_{1},b_{2}...b_{n}}
a
{\displaystyle a}
b
1
,
b
2
.
.
.
b
n
{\displaystyle b_{1},b_{2}...b_{n}}
a
{\displaystyle a}
Ex:
18
=
2
⋅
9
=
3
⋅
6
=
1
⋅
18
=
2
⋅
3
⋅
3
{\displaystyle 18=2\cdot 9=3\cdot 6=1\cdot 18=2\cdot 3\cdot 3}
A ideia da divisão euclidiana consiste em separar um todo em partes iguais. Essa divisão pode ocorrer de forma exata (quando a união dessas partes resulta no número original) ou de forma inexata (quando ocorre o contrário). No contexto dos números inteiros,
a
{\displaystyle a}
b
{\displaystyle b}
A divisão exata de
a
{\displaystyle a}
b
{\displaystyle b}
q
{\displaystyle q}
a
=
q
⋅
b
{\displaystyle a=q\cdot b}
{\displaystyle \qquad }
4
=
2
⋅
2
{\displaystyle \qquad \qquad 4=2\cdot 2}
10
=
2
⋅
5
{\displaystyle \qquad \qquad 10=2\cdot 5}
A divisão inexata de
a
{\displaystyle a}
b
{\displaystyle b}
q
{\displaystyle q}
a
=
q
⋅
b
+
r
{\displaystyle a=q\cdot b+r}
r
{\displaystyle r}
b
{\displaystyle b}
{\displaystyle \qquad }
26
=
2
⋅
9
+
8
{\displaystyle \qquad \qquad 26=2\cdot 9+8}
21
=
4
⋅
5
+
1
{\displaystyle \qquad \qquad 21=4\cdot 5+1}
Há apenas uma maneira de fazer uma divisão exata, mas há maneiras diferentes de se fazer uma divisão inexata. Podemos dividí-las em: inexatas por falta (como
17
=
3
⋅
5
+
2
{\displaystyle 17=3\cdot 5+2}
17
=
4
⋅
5
+
(
−
3
)
{\displaystyle 17=4\cdot 5+(-3)}
Este teorema afirma que os números primos funcionam como base para a construção de todo e qualquer número inteiro (exceto
0
{\displaystyle 0}
±
1
{\displaystyle \pm 1}
A fatoração em primos de um inteiro
a
≠
0
{\displaystyle a\neq 0}
±
1
{\displaystyle \pm 1}
Existem primos
p
1
,
p
2
,
p
3
,
.
.
.
,
{\displaystyle p_{1},p_{2},p_{3},...,}
a
=
±
p
1
⋅
p
2
⋅
p
3
.
.
.
{\displaystyle a=\pm p_{1}\cdot p_{2}\cdot p_{3}...}
Existem primos
p
1
≤
p
2
≤
p
3
≤
.
.
.
≤
p
n
{\displaystyle p_{1}\leq p_{2}\leq p_{3}\leq ...\leq p_{n}}
a
=
±
p
1
⋅
p
2
⋅
p
3
⋅
.
.
.
⋅
p
n
{\displaystyle a=\pm p_{1}\cdot p_{2}\cdot p_{3}\cdot ...\cdot p_{n}}
Existem primos distintos
p
1
<
p
2
<
p
3
,
.
.
.
<
p
n
{\displaystyle p_{1}<p_{2}<p_{3},...<p_{n}}
j
1
,
j
2
,
j
3
,
.
.
.
,
j
n
{\displaystyle j_{1},j_{2},j_{3},...,j_{n}}
a
=
±
p
1
j
1
⋅
p
2
j
2
⋅
p
3
j
3
⋅
.
.
.
⋅
p
n
j
n
{\displaystyle a=\pm p_{1}^{j_{1}}\cdot p_{2}^{j_{2}}\cdot p_{3}^{j_{3}}\cdot ...\cdot p_{n}^{j_{n}}}
Assim, por exemplo,
−
40
=
−
2
⋅
2
⋅
2
⋅
5
{\displaystyle \qquad \qquad -40=-2\cdot 2\cdot 2\cdot 5}
−
40
=
−
2
3
⋅
5
{\displaystyle \qquad \qquad -40=-2^{3}\cdot 5}
63
=
3
⋅
3
⋅
7
{\displaystyle \qquad \qquad 63=3\cdot 3\cdot 7}
63
=
3
2
⋅
7
{\displaystyle \qquad \qquad 63=3^{2}\cdot 7}
Na representação trigonométrica, um número complexo
z
=
a
+
i
b
{\displaystyle z=a+ib}
Um vetor é representado por um segmento de reta orientado, e define grandezas que se caracterizam por:
Módulo: Direção: Sentido: Quando
z
=
a
+
i
b
{\displaystyle z=a+ib}
Argumento de
z
{\displaystyle z}
θ
{\displaystyle \theta }
Módulo de
z
{\displaystyle z}
r
=
|
z
|
=
a
2
+
b
2
{\displaystyle r=|z|={\sqrt {a^{2}+b^{2}}}}
O argumento geral de
z
{\displaystyle z}
θ
+
2
π
.
k
{\displaystyle \theta +2\pi .k}
θ
+
k
.360
∘
{\displaystyle \theta +k.360^{\circ }}
argumento principal é o valor de
θ
{\displaystyle \theta }
−
π
<
θ
≤
π
{\displaystyle -\pi <\theta \leq \pi }
−
180
∘
<
θ
≤
180
∘
{\displaystyle -180^{\circ }<\theta \leq 180^{\circ }}
A partir das relações trigonométricas, obtêm-se:
cos
θ
=
a
|
z
|
{\displaystyle \cos \theta ={a \over |z|}}
a
=
|
z
|
.
cos
θ
{\displaystyle a=|z|.\cos \theta }
sen
θ
=
b
|
z
|
{\displaystyle \operatorname {sen} \theta ={b \over |z|}}
b
=
|
z
|
.
sen
θ
{\displaystyle b=|z|.\operatorname {sen} \theta }
Portanto, para o número complexo
z
=
a
+
i
b
{\displaystyle z=a+ib}
{\displaystyle \quad }
⇒
{\displaystyle \Rightarrow }
{\displaystyle \quad }
z
=
(
|
z
|
.
cos
θ
)
+
i
(
|
z
|
.
sen
θ
)
{\displaystyle z=(|z|.\cos \theta )+i(|z|.\operatorname {sen} \theta )}
Exemplos:
{\displaystyle \quad }
z
{\displaystyle z}
|
z
|
=
1
{\displaystyle |z|=1}
{\displaystyle \quad }
{\displaystyle \quad }
θ
=
0
+
2
π
k
{\displaystyle \theta =0+2\pi k}
|
z
|
=
1
{\displaystyle |z|=1}
{\displaystyle \quad }
{\displaystyle \quad }
z
=
1
{\displaystyle z=1}
z
=
cos
2
π
k
+
i
sen
2
π
k
{\displaystyle z=\cos 2\pi k+i\operatorname {sen} 2\pi k}
k
∈
Z
{\displaystyle k\in \mathbb {Z} }
{\displaystyle \quad }
{\displaystyle \quad }
z
{\displaystyle z}
{\displaystyle \quad }
{\displaystyle \quad }
z
=
1
{\displaystyle z=1}
{\displaystyle \quad }
{\displaystyle \quad }
z
=
cos
2
π
.0
+
i
sen
2
π
.0
{\displaystyle z=\cos 2\pi .0+i\operatorname {sen} 2\pi .0}
{\displaystyle \quad }
⇒
{\displaystyle \Rightarrow }
{\displaystyle \quad }
z
=
cos
0
+
i
sen
0
{\displaystyle z=\cos 0+i\operatorname {sen} 0}
{\displaystyle \quad }
{\displaystyle \quad }
z
=
cos
2
π
.1
+
i
sen
2
π
.1
{\displaystyle z=\cos 2\pi .1+i\operatorname {sen} 2\pi .1}
{\displaystyle \quad }
⇒
{\displaystyle \Rightarrow }
{\displaystyle \quad }
z
=
cos
2
π
+
i
sen
2
π
{\displaystyle z=\cos 2\pi +i\operatorname {sen} 2\pi }
{\displaystyle \quad }
{\displaystyle \quad }
z
=
cos
2
π
.2
+
i
sen
2
π
.2
{\displaystyle z=\cos 2\pi .2+i\operatorname {sen} 2\pi .2}
{\displaystyle \quad }
⇒
{\displaystyle \Rightarrow }
{\displaystyle \quad }
z
=
cos
4
π
+
i
sen
4
π
{\displaystyle z=\cos 4\pi +i\operatorname {sen} 4\pi }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
z
{\displaystyle z}
|
z
|
=
1
{\displaystyle |z|=1}
{\displaystyle \quad }
{\displaystyle \quad }
θ
=
1
2
π
+
2
π
k
{\displaystyle \theta ={\frac {1}{2}}\pi +2\pi k}
|
z
|
=
1
{\displaystyle |z|=1}
{\displaystyle \quad }
{\displaystyle \quad }
z
=
i
{\displaystyle z=i}
z
=
cos
(
1
2
π
+
2
π
k
)
+
i
sen
(
1
2
π
+
2
π
k
)
{\displaystyle z=\cos({\frac {1}{2}}\pi +2\pi k)+i\operatorname {sen}({\frac {1}{2}}\pi +2\pi k)}
k
∈
Z
{\displaystyle k\in \mathbb {Z} }
{\displaystyle \quad }
{\displaystyle \quad }
z
{\displaystyle z}
{\displaystyle \quad }
{\displaystyle \quad }
z
=
i
{\displaystyle z=i}
{\displaystyle \quad }
{\displaystyle \quad }
z
=
cos
(
1
2
π
+
2
π
.0
)
+
i
sen
(
1
2
π
+
2
π
.0
)
{\displaystyle z=\cos({\frac {1}{2}}\pi +2\pi .0)+i\operatorname {sen}({\frac {1}{2}}\pi +2\pi .0)}
{\displaystyle \quad }
⇒
{\displaystyle \Rightarrow }
{\displaystyle \quad }
z
=
cos
1
2
π
+
i
sen
1
2
π
{\displaystyle z=\cos {\frac {1}{2}}\pi +i\operatorname {sen} {\frac {1}{2}}\pi }
{\displaystyle \quad }
{\displaystyle \quad }
z
=
cos
(
1
2
π
+
2
π
.1
)
+
i
sen
(
1
2
π
+
2
π
.1
)
{\displaystyle z=\cos({\frac {1}{2}}\pi +2\pi .1)+i\operatorname {sen}({\frac {1}{2}}\pi +2\pi .1)}
{\displaystyle \quad }
⇒
{\displaystyle \Rightarrow }
{\displaystyle \quad }
z
=
cos
5
2
π
+
i
sen
5
2
π
{\displaystyle z=\cos {\frac {5}{2}}\pi +i\operatorname {sen} {\frac {5}{2}}\pi }
{\displaystyle \quad }
{\displaystyle \quad }
z
=
cos
(
1
2
π
+
2
π
.2
)
+
i
sen
(
1
2
π
+
2
π
.2
)
{\displaystyle z=\cos({\frac {1}{2}}\pi +2\pi .2)+i\operatorname {sen}({\frac {1}{2}}\pi +2\pi .2)}
{\displaystyle \quad }
⇒
{\displaystyle \Rightarrow }
{\displaystyle \quad }
z
=
cos
9
2
π
+
i
sen
9
2
π
{\displaystyle z=\cos {\frac {9}{2}}\pi +i\operatorname {sen} {\frac {9}{2}}\pi }
{\displaystyle \qquad }
{\displaystyle \qquad }
Dados dois números complexos
z
=
a
+
i
b
{\displaystyle z=a+ib}
w
=
c
+
i
d
{\displaystyle w=c+id}
{\displaystyle \quad }
z
=
|
z
|
(
cos
(
θ
+
2
π
k
)
+
i
sen
(
θ
+
2
π
k
)
)
{\displaystyle z=|z|(\cos(\theta +2\pi k)+i\operatorname {sen}(\theta +2\pi k))}
{\displaystyle \quad }
w
=
|
w
|
(
cos
(
α
+
2
π
k
)
+
i
sen
(
α
+
2
π
k
)
)
{\displaystyle w=|w|(\cos(\alpha +2\pi k)+i\operatorname {sen}(\alpha +2\pi k))}
{\displaystyle \quad }
z
=
w
{\displaystyle z=w}
{\displaystyle \quad }
⇔
{\displaystyle \Leftrightarrow }
{\displaystyle \quad }
|
z
|
cos
θ
=
|
w
|
cos
α
{\displaystyle |z|\cos \theta =|w|\cos \alpha }
|
z
|
sen
θ
=
|
w
|
sen
α
{\displaystyle |z|\operatorname {sen} \theta =|w|\operatorname {sen} \alpha }
{\displaystyle \quad }
⇔
{\displaystyle \Leftrightarrow }
{\displaystyle \quad }
|
z
|
=
|
w
|
{\displaystyle |z|=|w|}
α
=
θ
+
2
π
k
{\displaystyle \alpha =\theta +2\pi k}
A igualdade exige que
|
z
|
=
|
w
|
{\displaystyle |z|=|w|}
θ
=
α
{\displaystyle \theta =\alpha }
O simétrico de um número complexo
z
=
a
+
i
b
{\displaystyle z=a+ib}
−
z
=
−
(
a
+
i
b
)
{\displaystyle -z=-(a+ib)}
−
z
=
(
−
a
)
+
i
(
−
b
)
{\displaystyle -z=(-a)+i(-b)}
Corresponde a uma rotação de 180° em torno da origem, à partir de
z
{\displaystyle z}
Em notação trigonométrica:
z
=
|
z
|
(
cos
θ
+
i
sen
θ
)
{\displaystyle z=|z|(\cos \theta +i\operatorname {sen} \theta )}
(
−
z
)
=
|
z
|
(
cos
(
θ
+
π
)
+
i
sen
(
θ
+
π
)
)
{\displaystyle (-z)=|z|(\cos(\theta +\pi )+i\operatorname {sen}(\theta +\pi ))}
Exemplo:
z
=
1
+
i
=
|
z
|
(
cos
θ
+
i
sen
θ
)
=
2
(
cos
π
4
+
i
sen
π
4
)
{\displaystyle z=1+i=|z|(\cos \theta +i\operatorname {sen} \theta )={\sqrt {2}}(\cos {\frac {\pi }{4}}+i\operatorname {sen} {\frac {\pi }{4}})}
(
−
z
)
=
−
1
−
i
=
|
z
|
(
cos
(
θ
+
π
)
+
i
sen
(
θ
+
π
)
)
=
2
(
cos
5
4
π
+
i
sen
5
4
π
)
{\displaystyle (-z)=-1-i=|z|(\cos(\theta +\pi )+i\operatorname {sen}(\theta +\pi ))={\sqrt {2}}(\cos {\frac {5}{4}}\pi +i\operatorname {sen} {\frac {5}{4}}\pi )}
O conjugado de um número complexo
z
=
a
+
i
b
{\displaystyle z=a+ib}
z
¯
=
a
−
i
b
{\displaystyle {\bar {z}}=a-ib}
Corresponde a uma reflexão de
z
{\displaystyle z}
Em notação trigonométrica:
z
=
|
z
|
(
cos
θ
+
i
sen
θ
)
{\displaystyle z=|z|(\cos \theta +i\operatorname {sen} \theta )}
z
¯
=
|
z
|
(
cos
(
−
θ
)
+
i
sen
(
−
θ
)
)
{\displaystyle {\bar {z}}=|z|(\cos(-\theta )+i\operatorname {sen}(-\theta ))}
Exemplo:
z
=
1
+
i
=
|
z
|
(
cos
θ
+
i
sen
θ
)
=
2
(
cos
π
4
+
i
sen
π
4
)
{\displaystyle z=1+i=|z|(\cos \theta +i\operatorname {sen} \theta )={\sqrt {2}}(\cos {\frac {\pi }{4}}+i\operatorname {sen} {\frac {\pi }{4}})}
z
¯
=
−
1
−
i
=
|
z
|
(
cos
(
−
θ
)
+
i
sen
(
−
θ
)
)
=
2
(
cos
(
−
5
4
)
π
+
i
sen
(
−
5
4
)
π
)
{\displaystyle {\bar {z}}=-1-i=|z|(\cos(-\theta )+i\operatorname {sen}(-\theta ))={\sqrt {2}}(\cos(-{\frac {5}{4}})\pi +i\operatorname {sen}(-{\frac {5}{4}})\pi )}
Seja
z
=
|
z
|
(
cos
θ
+
i
sen
θ
)
{\displaystyle z=|z|(\cos \theta +i\operatorname {sen} \theta )}
w
=
|
w
|
(
cos
α
+
i
sen
α
)
{\displaystyle w=|w|(\cos \alpha +i\operatorname {sen} \alpha )}
O produto de um número complexo Z por um número real K: [ editar | editar código-fonte ]
{\displaystyle \quad }
{\displaystyle \quad }
k
.
z
=
k
.
|
z
|
(
cos
θ
+
i
sen
θ
)
{\displaystyle k.z=k.|z|(\cos \theta +i\operatorname {sen} \theta )}
Se
k
>
1
{\displaystyle k>1}
z
{\displaystyle z}
Exemplo:
z
=
1
+
i
=
|
z
|
(
cos
θ
+
i
sen
θ
)
=
2
(
cos
45
∘
+
i
sen
45
∘
)
{\displaystyle z=1+i=|z|(\cos \theta +i\operatorname {sen} \theta )={\sqrt {2}}(\cos 45^{\circ }+i\operatorname {sen} 45^{\circ })}
2.
z
=
2
+
2
i
=
2.
|
z
|
(
cos
θ
+
i
sen
θ
)
=
2
2
(
cos
45
∘
+
i
sen
45
∘
)
{\displaystyle 2.z=2+2i=2.|z|(\cos \theta +i\operatorname {sen} \theta )=2{\sqrt {2}}(\cos 45^{\circ }+i\operatorname {sen} 45^{\circ })}
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
Se
0
<
k
<
1
{\displaystyle 0<k<1}
z
{\displaystyle z}
Exemplo:
z
=
1
+
i
=
|
z
|
(
cos
θ
+
i
sen
θ
)
=
2
(
cos
45
∘
+
i
sen
45
∘
)
{\displaystyle z=1+i=|z|(\cos \theta +i\operatorname {sen} \theta )={\sqrt {2}}(\cos 45^{\circ }+i\operatorname {sen} 45^{\circ })}
1
2
.
z
=
1
2
+
1
2
i
=
1
2
.
|
z
|
(
cos
θ
+
i
sen
θ
)
=
2
2
(
cos
45
∘
+
i
sen
45
∘
)
{\displaystyle {\frac {1}{2}}.z={\frac {1}{2}}+{\frac {1}{2}}i={\frac {1}{2}}.|z|(\cos \theta +i\operatorname {sen} \theta )={\frac {\sqrt {2}}{2}}(\cos 45^{\circ }+i\operatorname {sen} 45^{\circ })}
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
Se
k
<
0
{\displaystyle k<0}
z
{\displaystyle z}
180
∘
{\displaystyle 180^{\circ }}
z
{\displaystyle z}
−
z
{\displaystyle -z}
Exemplo:
z
=
1
+
i
=
|
z
|
(
cos
θ
+
i
sen
θ
)
=
2
(
cos
45
∘
+
i
sen
45
∘
)
{\displaystyle z=1+i=|z|(\cos \theta +i\operatorname {sen} \theta )={\sqrt {2}}(\cos 45^{\circ }+i\operatorname {sen} 45^{\circ })}
(
−
1
)
.
z
=
−
(
1
+
1
i
)
=
|
z
|
(
cos
(
θ
+
180
∘
)
+
i
sen
(
θ
+
180
∘
)
)
=
2
(
cos
225
∘
+
i
sen
225
∘
)
{\displaystyle (-1).z=-(1+1i)=|z|(\cos(\theta +180^{\circ })+i\operatorname {sen}(\theta +180^{\circ }))={\sqrt {2}}(\cos 225^{\circ }+i\operatorname {sen} 225^{\circ })}
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
O produto de um número complexo Z por um imaginário puro [ editar | editar código-fonte ] Dados
z
=
|
z
|
(
cos
θ
+
i
sen
θ
)
{\displaystyle z=|z|(\cos \theta +i\operatorname {sen} \theta )}
w
=
|
w
|
(
cos
90
∘
+
i
sen
90
∘
)
{\displaystyle w=|w|(\cos 90^{\circ }+i\operatorname {sen} 90^{\circ })}
{\displaystyle \quad }
{\displaystyle \quad }
z
.
w
=
|
z
|
(
cos
θ
+
i
sen
θ
)
|
w
|
(
cos
90
∘
+
i
sen
90
∘
)
{\displaystyle z.w=|z|(\cos \theta +i\operatorname {sen} \theta )|w|(\cos 90^{\circ }+i\operatorname {sen} 90^{\circ })}
{\displaystyle \quad }
{\displaystyle \quad }
z
.
w
=
|
z
|
|
w
|
[
(
cos
θ
.
cos
90
∘
−
sen
θ
.
cos
90
∘
)
+
i
(
cos
θ
.
cos
90
∘
+
sen
θ
.
cos
90
∘
)
{\displaystyle z.w=|z||w|[(\cos \theta .\cos 90^{\circ }-\operatorname {sen} \theta .\cos 90^{\circ })+i(\cos \theta .\cos 90^{\circ }+\operatorname {sen} \theta .\cos 90^{\circ })}
A partir desta etapa, é necessário utilizar a expressão trigonométrica da soma dos ângulos dos senos e cossenos:
{\displaystyle \quad }
{\displaystyle \quad }
cos
(
θ
+
α
)
=
cos
θ
.
cos
α
−
sen
θ
.
sen
α
{\displaystyle \cos(\theta +\alpha )=\cos \theta .\cos \alpha -\operatorname {sen} \theta .\operatorname {sen} \alpha }
{\displaystyle \quad }
{\displaystyle \quad }
sen
(
θ
+
α
)
=
cos
θ
.
sen
α
+
cos
α
.
sen
θ
{\displaystyle \operatorname {sen}(\theta +\alpha )=\cos \theta .\operatorname {sen} \alpha +\cos \alpha .\operatorname {sen} \theta }
Logo,
{\displaystyle \quad }
{\displaystyle \quad }
cos
(
θ
+
90
∘
)
=
cos
θ
.
cos
90
∘
−
sen
θ
.
sen
90
∘
{\displaystyle \cos(\theta +90^{\circ })=\cos \theta .\cos 90^{\circ }-\operatorname {sen} \theta .\operatorname {sen} 90^{\circ }}
{\displaystyle \quad }
{\displaystyle \quad }
sen
(
θ
+
90
∘
)
=
cos
θ
.
sen
90
∘
+
cos
90
∘
.
sen
θ
{\displaystyle \operatorname {sen}(\theta +90^{\circ })=\cos \theta .\operatorname {sen} 90^{\circ }+\cos 90^{\circ }.\operatorname {sen} \theta }
Então,
{\displaystyle \quad }
{\displaystyle \quad }
z
.
w
=
|
z
|
|
w
|
[
(
cos
θ
.
cos
90
∘
−
sen
θ
.
cos
90
∘
)
+
i
(
cos
θ
.
cos
90
∘
+
sen
θ
.
cos
90
∘
)
{\displaystyle z.w=|z||w|[(\cos \theta .\cos 90^{\circ }-\operatorname {sen} \theta .\cos 90^{\circ })+i(\cos \theta .\cos 90^{\circ }+\operatorname {sen} \theta .\cos 90^{\circ })}
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
=
|
z
|
|
w
|
(
cos
(
θ
+
90
∘
)
+
i
sen
(
θ
+
90
∘
)
)
{\displaystyle =|z||w|(\cos(\theta +90^{\circ })+i\operatorname {sen}(\theta +90^{\circ }))}
O produto de um número complexo por um número imaginário puro corresponde a uma ampliação ou contração do vetor, seguido de uma rotação de
90
∘
{\displaystyle 90^{\circ }}
(colocar gif)
O produto de um número complexo genérico Z por um outro número complexo W [ editar | editar código-fonte ] Dados
z
=
|
z
|
(
cos
θ
+
i
sen
θ
)
{\displaystyle z=|z|(\cos \theta +i\operatorname {sen} \theta )}
w
=
|
w
|
(
cos
α
+
i
sen
α
)
{\displaystyle w=|w|(\cos \alpha +i\operatorname {sen} \alpha )}
{\displaystyle \quad }
{\displaystyle \quad }
z
.
w
=
|
z
|
(
cos
θ
+
i
sen
θ
)
|
w
|
(
cos
α
+
i
sen
α
)
{\displaystyle z.w=|z|(\cos \theta +i\operatorname {sen} \theta )|w|(\cos \alpha +i\operatorname {sen} \alpha )}
{\displaystyle \quad }
{\displaystyle \quad }
z
.
w
=
|
z
|
|
w
|
[
(
cos
θ
.
cos
α
−
sen
θ
.
cos
α
)
+
i
(
cos
θ
.
cos
α
+
sen
θ
.
cos
α
)
{\displaystyle z.w=|z||w|[(\cos \theta .\cos \alpha -\operatorname {sen} \theta .\cos \alpha )+i(\cos \theta .\cos \alpha +\operatorname {sen} \theta .\cos \alpha )}
Assim como no caso anterior, é necessário utilizar a soma dos angulos dos senos e cossenos.
Logo,
{\displaystyle \quad }
{\displaystyle \quad }
z
.
w
=
|
z
|
|
w
|
(
cos
(
θ
+
α
)
+
i
sen
(
θ
+
α
)
)
{\displaystyle z.w=|z||w|(\cos(\theta +\alpha )+i\operatorname {sen}(\theta +\alpha ))}
O produto de um número complexo
z
{\displaystyle z}
w
{\displaystyle w}
w
{\displaystyle w}
(colocar gif)
A soma de números complexos corresponde à soma dos vetores complexos associados a esses números.
Dados quaisquer números reais
z
{\displaystyle z}
O
A
→
{\displaystyle {\vec {OA}}}
w
{\displaystyle w}
O
B
→
{\displaystyle {\vec {OB}}}
z
+
w
{\displaystyle z+w}
O
C
→
{\displaystyle {\vec {OC}}}
O
A
→
+
O
B
→
=
O
C
→
{\displaystyle {\vec {OA}}+{\vec {OB}}={\vec {OC}}}
Exemplos:
z
=
O
A
→
=
1
+
3
i
{\displaystyle z={\vec {OA}}=1+3i}
w
=
O
B
→
=
5
+
1
i
{\displaystyle w={\vec {OB}}=5+1i}
z
+
w
=
O
A
→
+
O
B
→
=
O
C
→
=
6
+
4
i
{\displaystyle z+w={\vec {OA}}+{\vec {OB}}={\vec {OC}}=6+4i}
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
z
=
O
A
→
=
−
2
+
2
i
{\displaystyle z={\vec {OA}}=-2+2i}
w
=
O
B
→
=
4
+
2
i
{\displaystyle w={\vec {OB}}=4+2i}
z
+
w
=
O
A
→
+
O
B
→
=
O
C
→
=
2
+
4
i
{\displaystyle z+w={\vec {OA}}+{\vec {OB}}={\vec {OC}}=2+4i}
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
z
=
O
A
→
=
−
2
+
2
i
{\displaystyle z={\vec {OA}}=-2+2i}
w
=
O
B
→
=
4
−
1
i
{\displaystyle w={\vec {OB}}=4-1i}
z
+
w
=
O
A
→
+
O
B
→
=
O
C
→
=
2
+
1
i
{\displaystyle z+w={\vec {OA}}+{\vec {OB}}={\vec {OC}}=2+1i}
{\displaystyle \quad }
{\displaystyle \quad }
O comprimento de um vetor
v
→
{\displaystyle {\overrightarrow {v}}}
v
→
{\displaystyle {\overrightarrow {v}}}
v
→
{\displaystyle {\overrightarrow {v}}}
|
v
→
|
{\displaystyle |{\overrightarrow {v}}|}
|
v
→
|
=
v
1
2
+
v
2
2
{\displaystyle |{\overrightarrow {v}}|={\sqrt {v_{1}^{2}+v_{2}^{2}}}}
v
→
=
(
v
1
,
v
2
)
{\displaystyle {\overrightarrow {v}}=(v_{1},v_{2})}
|
v
→
|
=
v
1
2
+
v
2
2
+
v
3
2
{\displaystyle |{\overrightarrow {v}}|={\sqrt {v_{1}^{2}+v_{2}^{2}+v_{3}^{2}}}}
v
→
=
(
v
1
,
v
2
,
v
3
)
{\displaystyle {\overrightarrow {v}}=(v_{1},v_{2},v_{3})}
A distância entre dois pontos do plano,
P
=
(
x
1
,
y
1
)
{\displaystyle P=(x_{1},y_{1})}
Q
=
(
x
2
,
y
2
)
{\displaystyle Q=(x_{2},y_{2})}
P
Q
→
{\displaystyle {\overrightarrow {PQ}}}
P
Q
→
=
Q
−
P
=
(
x
2
−
x
1
,
y
2
−
y
1
)
{\displaystyle {\overrightarrow {PQ}}=Q-P=(x_{2}-x_{1},y_{2}-y_{1})}
P
{\displaystyle P}
Q
{\displaystyle Q}
d
i
s
t
(
P
,
Q
)
=
|
P
Q
→
|
=
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
{\displaystyle dist(P,Q)=|{\overrightarrow {PQ}}|={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}}
Exemplo:
Dados os pontos do plano
P
=
(
0
,
0
)
{\displaystyle P=(0,0)}
Q
=
(
4
,
2
)
{\displaystyle Q=(4,2)}
A distância entre os pontos é igual a norma do vetor
P
Q
→
{\displaystyle {\overrightarrow {PQ}}}
d
i
s
t
(
P
,
Q
)
=
|
P
Q
→
|
{\displaystyle dist(P,Q)=|{\overrightarrow {PQ}}|}
P
Q
→
=
(
4
−
0
,
2
−
0
)
{\displaystyle {\overrightarrow {PQ}}=(4-0,2-0)}
|
P
Q
→
|
=
(
4
−
0
)
2
+
(
2
−
0
)
2
{\displaystyle |{\overrightarrow {PQ}}|={\sqrt {(4-0)^{2}+(2-0)^{2}}}}
d
i
s
t
(
P
,
Q
)
=
(
4
−
0
)
2
+
(
2
−
0
)
2
{\displaystyle dist(P,Q)={\sqrt {(4-0)^{2}+(2-0)^{2}}}}
d
i
s
t
(
P
,
Q
)
=
(
4
2
+
2
2
)
{\displaystyle dist(P,Q)={\sqrt {(4^{2}+2^{2})}}}
d
i
s
t
(
P
,
Q
)
=
(
16
+
4
)
{\displaystyle dist(P,Q)={\sqrt {(16+4)}}}
d
i
s
t
(
P
,
Q
)
=
(
20
)
{\displaystyle dist(P,Q)={\sqrt {(20)}}}
d
i
s
t
(
P
,
Q
)
=
2
5
{\displaystyle dist(P,Q)=2{\sqrt {5}}}
A distância entre dois pontos no espaço,
P
=
(
x
1
,
y
1
,
z
1
)
{\displaystyle P=(x_{1},y_{1},z_{1})}
Q
=
(
x
2
,
y
2
,
z
2
)
{\displaystyle Q=(x_{2},y_{2},z_{2})}
P
Q
→
{\displaystyle {\overrightarrow {PQ}}}
P
Q
→
=
Q
−
P
=
(
x
2
−
x
1
,
y
2
−
y
1
,
z
2
−
z
1
)
{\displaystyle {\overrightarrow {PQ}}=Q-P=(x_{2}-x_{1},y_{2}-y_{1},z_{2}-z_{1})}
P
{\displaystyle P}
Q
{\displaystyle Q}
d
i
s
t
(
P
,
Q
)
=
|
P
Q
→
|
=
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
+
(
z
2
−
z
1
)
2
{\displaystyle dist(P,Q)=|{\overrightarrow {PQ}}|={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}}}
(Colocar Imagem)
O produto escalar de dois vetores
u
→
{\displaystyle {\overrightarrow {u}}}
v
→
{\displaystyle {\overrightarrow {v}}}
u
→
.
v
→
=
{
0
,
se
u
→
ou
v
→
é o vetor nulo
|
u
→
|
|
v
→
|
c
o
s
θ
,
caso nenhum deles seja nulo
{\displaystyle {\overrightarrow {u}}.{\overrightarrow {v}}={\begin{cases}0,&{\text{ se }}{\overrightarrow {u}}{\text{ ou }}{\overrightarrow {v}}{\text{ é o vetor nulo}}\\|{\overrightarrow {u}}||{\overrightarrow {v}}|cos\theta ,&{\text{ caso nenhum deles seja nulo}}\end{cases}}}
θ
{\displaystyle \theta }
Quando os vetores são dados em termos das suas componentes, não há como sabermos diretamente o ângulo entre eles. Para descobrir, é necessário uma forma de calcular o produto escalar que não necessite do ângulo entre os vetores.
Se
u
→
{\displaystyle {\overrightarrow {u}}}
v
→
{\displaystyle {\overrightarrow {v}}}
θ
{\displaystyle \theta }
|
u
→
−
v
→
|
2
=
|
u
→
|
2
+
|
v
→
|
2
−
2
|
u
→
|
|
v
→
|
c
o
s
θ
{\displaystyle |{\overrightarrow {u}}-{\overrightarrow {v}}|^{2}=|{\overrightarrow {u}}|^{2}+|{\overrightarrow {v}}|^{2}-2|{\overrightarrow {u}}||{\overrightarrow {v}}|cos\theta }
Assim,
u
→
.
v
→
=
|
u
→
|
|
v
→
|
c
o
s
θ
=
1
2
(
|
u
→
|
2
+
|
v
→
|
2
−
|
u
→
−
v
→
|
2
)
{\displaystyle {\overrightarrow {u}}.{\overrightarrow {v}}=|{\overrightarrow {u}}||{\overrightarrow {v}}|cos\theta ={\frac {1}{2}}(|{\overrightarrow {u}}|^{2}+|{\overrightarrow {v}}|^{2}-|{\overrightarrow {u}}-{\overrightarrow {v}}|^{2})}
Substituindo-se as coordenadas dos vetores, obtemos uma expressão mais simples para o cálculo do produto interno.
Sendo
v
→
=
(
v
1
,
v
2
,
v
3
)
{\displaystyle {\vec {v}}=(v_{1},v_{2},v_{3})}
u
→
=
(
u
1
,
u
2
,
u
3
)
{\displaystyle {\vec {u}}=(u_{1},u_{2},u_{3})}
|
v
→
|
2
=
v
1
2
+
v
2
2
+
v
3
2
{\displaystyle |{\vec {v}}|^{2}=v_{1}^{2}+v_{2}^{2}+v_{3}^{2}}
|
u
→
|
2
=
u
1
2
+
u
2
2
+
u
3
2
{\displaystyle |{\vec {u}}|^{2}=u_{1}^{2}+u_{2}^{2}+u_{3}^{2}}
|
v
→
−
u
→
|
2
=
(
v
1
−
u
1
)
2
+
(
v
2
−
u
2
)
2
+
(
v
3
−
u
3
)
2
{\displaystyle |{\vec {v}}-{\vec {u}}|^{2}=(v_{1}-u_{1})^{2}+(v_{2}-u_{2})^{2}+(v_{3}-u_{3})^{2}}
obtemos,
{\displaystyle \quad }
u
→
.
v
→
=
1
2
(
|
u
→
|
2
+
|
v
→
|
2
−
|
u
→
−
v
→
|
2
)
{\displaystyle {\overrightarrow {u}}.{\overrightarrow {v}}={\frac {1}{2}}(|{\overrightarrow {u}}|^{2}+|{\overrightarrow {v}}|^{2}-|{\overrightarrow {u}}-{\overrightarrow {v}}|^{2})}
⇒
{\displaystyle \Rightarrow }
u
→
.
v
→
=
1
2
(
u
1
2
+
u
2
2
+
u
3
2
+
v
1
2
+
v
2
2
+
v
3
2
−
(
(
u
1
−
v
1
)
2
+
(
u
2
−
v
2
)
2
+
(
u
3
−
v
3
)
2
)
)
{\displaystyle {\overrightarrow {u}}.{\overrightarrow {v}}={\frac {1}{2}}(u_{1}^{2}+u_{2}^{2}+u_{3}^{2}+v_{1}^{2}+v_{2}^{2}+v_{3}^{2}-((u_{1}-v_{1})^{2}+(u_{2}-v_{2})^{2}+(u_{3}-v_{3})^{2}))}
⇒
{\displaystyle \Rightarrow }
u
→
.
v
→
=
1
2
(
u
1
2
+
u
2
2
+
u
3
2
+
v
1
2
+
v
2
2
+
v
3
2
−
(
u
1
2
−
2
u
1
v
1
+
v
1
2
+
u
2
2
−
2
u
2
v
2
+
v
2
2
+
u
3
2
−
2
u
3
v
3
+
v
3
2
)
{\displaystyle {\overrightarrow {u}}.{\overrightarrow {v}}={\frac {1}{2}}(u_{1}^{2}+u_{2}^{2}+u_{3}^{2}+v_{1}^{2}+v_{2}^{2}+v_{3}^{2}-(u_{1}^{2}-2u_{1}v_{1}+v_{1}^{2}+u_{2}^{2}-2u_{2}v_{2}+v_{2}^{2}+u_{3}^{2}-2u_{3}v_{3}+v_{3}^{2})}
⇒
{\displaystyle \Rightarrow }
u
→
.
v
→
=
1
2
(
u
1
2
+
u
2
2
+
u
3
2
+
v
1
2
+
v
2
2
+
v
3
2
−
u
1
2
+
2
u
1
v
1
−
v
1
2
−
u
2
2
+
2
u
2
v
2
−
v
2
2
−
u
3
2
+
2
u
3
v
3
−
v
3
2
)
{\displaystyle {\overrightarrow {u}}.{\overrightarrow {v}}={\frac {1}{2}}(u_{1}^{2}+u_{2}^{2}+u_{3}^{2}+v_{1}^{2}+v_{2}^{2}+v_{3}^{2}-u_{1}^{2}+2u_{1}v_{1}-v_{1}^{2}-u_{2}^{2}+2u_{2}v_{2}-v_{2}^{2}-u_{3}^{2}+2u_{3}v_{3}-v_{3}^{2})}
⇒
{\displaystyle \Rightarrow }
u
→
.
v
→
=
1
2
(
2
u
1
v
1
+
2
u
2
v
2
+
2
u
3
v
3
)
{\displaystyle {\overrightarrow {u}}.{\overrightarrow {v}}={\frac {1}{2}}(2u_{1}v_{1}+2u_{2}v_{2}+2u_{3}v_{3})}
⇒
{\displaystyle \Rightarrow }
u
→
.
v
→
=
u
1
v
1
+
u
2
v
2
+
u
3
v
3
{\displaystyle {\overrightarrow {u}}.{\overrightarrow {v}}=u_{1}v_{1}+u_{2}v_{2}+u_{3}v_{3}}
{\displaystyle \quad }
O produto escalar,
u
→
.
v
→
{\displaystyle {\overrightarrow {u}}.{\overrightarrow {v}}}
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
u
→
.
v
→
=
u
1
v
1
+
u
2
v
2
{\displaystyle {\overrightarrow {u}}.{\overrightarrow {v}}=u_{1}v_{1}+u_{2}v_{2}}
se
u
→
=
(
u
1
,
u
2
)
{\displaystyle {\overrightarrow {u}}=(u_{1},u_{2})}
v
→
=
(
v
1
,
v
2
)
{\displaystyle {\overrightarrow {v}}=(v_{1},v_{2})}
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
{\displaystyle \quad }
u
→
.
v
→
=
u
1
v
1
+
u
2
v
2
+
u
3
v
3
{\displaystyle {\overrightarrow {u}}.{\overrightarrow {v}}=u_{1}v_{1}+u_{2}v_{2}+u_{3}v_{3}}
se
u
→
=
(
u
1
,
u
2
,
u
3
)
{\displaystyle {\overrightarrow {u}}=(u_{1},u_{2},u_{3})}
v
→
=
(
v
1
,
v
2
,
v
3
)
{\displaystyle {\overrightarrow {v}}=(v_{1},v_{2},v_{3})}
{\displaystyle \quad }
Sejam
u
→
{\displaystyle {\overrightarrow {u}}}
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
α
{\displaystyle \alpha }
Comutatividade :
u
→
.
v
→
=
v
→
.
u
→
{\displaystyle {\overrightarrow {u}}.{\overrightarrow {v}}={\overrightarrow {v}}.{\overrightarrow {u}}}
Demonstração:
u
→
.
v
→
=
u
1
v
1
+
u
2
v
2
{\displaystyle \quad {\overrightarrow {u}}.{\overrightarrow {v}}=u_{1}v_{1}+u_{2}v_{2}}
=
v
1
u
1
+
v
2
u
2
{\displaystyle =v_{1}u_{1}+v_{2}u_{2}}
=
v
→
.
u
→
{\displaystyle ={\overrightarrow {v}}.{\overrightarrow {u}}}
Distributividade:
u
→
.
(
v
→
+
w
→
)
=
u
→
.
v
→
+
u
→
.
w
→
{\displaystyle {\overrightarrow {u}}.({\overrightarrow {v}}+{\overrightarrow {w}})={\overrightarrow {u}}.{\overrightarrow {v}}+{\overrightarrow {u}}.{\overrightarrow {w}}}
Demonstração:
u
→
.
(
v
→
+
w
→
)
=
(
u
1
u
2
)
.
(
v
1
+
w
1
,
v
2
+
w
2
)
=
u
1
.
(
v
1
+
w
1
)
+
u
2
.
(
v
2
+
w
2
)
=
(
u
1
v
1
+
u
1
w
1
)
+
(
u
2
v
2
+
u
2
w
2
)
=
(
u
1
v
1
+
u
2
v
2
)
+
(
u
1
w
1
+
u
2
w
2
)
=
u
→
.
v
→
+
u
→
.
w
→
{\displaystyle \quad {\overrightarrow {u}}.({\overrightarrow {v}}+{\overrightarrow {w}})=(u_{1}u_{2}).(v_{1}+w_{1},v_{2}+w_{2})=u_{1}.(v_{1}+w_{1})+u_{2}.(v_{2}+w_{2})=(u_{1}v_{1}+u_{1}w_{1})+(u_{2}v_{2}+u_{2}w_{2})=(u_{1}v_{1}+u_{2}v_{2})+(u_{1}w_{1}+u_{2}w_{2})={\overrightarrow {u}}.{\overrightarrow {v}}+{\overrightarrow {u}}.{\overrightarrow {w}}}
Associatividade:
α
(
u
→
.
v
→
)
=
(
α
u
→
)
.
v
→
=
(
α
v
→
)
.
u
→
{\displaystyle \alpha ({\overrightarrow {u}}.{\overrightarrow {v}})=(\alpha {\overrightarrow {u}}).{\overrightarrow {v}}=(\alpha {\overrightarrow {v}}).{\overrightarrow {u}}}
Demonstração:
α
.
(
u
→
.
v
→
)
=
α
.
(
u
1
v
1
+
u
2
v
2
)
=
(
α
u
1
)
.
v
1
+
(
α
u
2
)
.
v
2
=
(
α
u
→
)
.
v
→
=
(
α
v
→
)
.
u
→
{\displaystyle \quad \alpha .({\overrightarrow {u}}.{\overrightarrow {v}})=\alpha .(u_{1}v_{1}+u_{2}v_{2})=(\alpha u_{1}).v_{1}+(\alpha u_{2}).v_{2}=(\alpha {\overrightarrow {u}}).{\overrightarrow {v}}=(\alpha {\overrightarrow {v}}).{\overrightarrow {u}}}
Dados dois vetores
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
projeção ortogonal de
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
, denotada por
p
r
o
j
w
→
v
→
{\displaystyle proj_{\overrightarrow {w}}^{\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
v
→
−
p
r
o
j
w
→
v
→
{\displaystyle {\overrightarrow {v}}-proj_{\overrightarrow {w}}^{\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
Seja
w
→
{\displaystyle {\overrightarrow {w}}}
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
p
r
o
j
w
→
v
→
=
(
v
→
.
w
→
|
w
→
|
2
)
.
w
→
{\displaystyle proj_{\overrightarrow {w}}^{\overrightarrow {v}}=\left({\frac {{\overrightarrow {v}}.{\overrightarrow {w}}}{|{\overrightarrow {w}}|^{2}}}\right).{\overrightarrow {w}}}
Demonstração:
Sejam
v
→
1
=
p
r
o
j
w
→
v
→
{\displaystyle {\overrightarrow {v}}_{1}=proj_{\overrightarrow {w}}^{\overrightarrow {v}}}
v
→
2
=
v
→
−
p
r
o
j
w
→
v
→
{\displaystyle {\overrightarrow {v}}_{2}={\overrightarrow {v}}-proj_{\overrightarrow {w}}^{\overrightarrow {v}}}
v
→
1
{\displaystyle {\overrightarrow {v}}_{1}}
w
→
{\displaystyle {\overrightarrow {w}}}
v
→
1
=
α
w
→
{\displaystyle \qquad {\overrightarrow {v}}_{1}=\alpha {\overrightarrow {w}}}
v
→
2
=
v
→
−
α
w
→
{\displaystyle {\overrightarrow {v}}_{2}={\overrightarrow {v}}-\alpha {\overrightarrow {w}}}
Multiplicando-se escalarmente
v
→
2
{\displaystyle {\overrightarrow {v}}_{2}}
w
→
{\displaystyle {\overrightarrow {w}}}
v
→
2
.
w
→
=
(
v
→
−
α
w
→
)
.
w
→
=
v
→
.
w
→
−
α
|
w
→
|
2
{\displaystyle \qquad {\overrightarrow {v}}_{2}.{\overrightarrow {w}}=({\overrightarrow {v}}-\alpha {\overrightarrow {w}}).{\overrightarrow {w}}={\overrightarrow {v}}.{\overrightarrow {w}}-\alpha |{\overrightarrow {w}}|^{2}}
v
→
2
{\displaystyle {\overrightarrow {v}}_{2}}
w
→
{\displaystyle {\overrightarrow {w}}}
v
→
2
.
w
→
=
0
{\displaystyle {\overrightarrow {v}}_{2}.{\overrightarrow {w}}=0}
α
=
v
→
.
w
→
|
w
→
|
2
{\displaystyle \qquad \alpha ={\frac {{\overrightarrow {v}}.{\overrightarrow {w}}}{|{\overrightarrow {w}}|^{2}}}}
Substituindo na equação
v
→
1
=
α
w
→
{\displaystyle {\overrightarrow {v}}_{1}=\alpha {\overrightarrow {w}}}
p
r
o
j
w
→
v
→
=
(
v
→
.
w
→
|
w
→
|
2
)
.
w
→
{\displaystyle \qquad proj_{\overrightarrow {w}}^{\overrightarrow {v}}=\left({\frac {{\overrightarrow {v}}.{\overrightarrow {w}}}{|{\overrightarrow {w}}|^{2}}}\right).{\overrightarrow {w}}}
Exemplo:
Sejam
v
→
=
(
2
,
−
1
,
3
)
{\displaystyle {\overrightarrow {v}}=(2,-1,3)}
w
→
=
(
4
,
−
1
,
2
)
{\displaystyle {\overrightarrow {w}}=(4,-1,2)}
v
→
1
{\displaystyle {\overrightarrow {v}}_{1}}
v
→
2
{\displaystyle {\overrightarrow {v}}_{2}}
v
→
=
v
→
1
+
v
→
2
{\displaystyle {\overrightarrow {v}}={\overrightarrow {v}}_{1}+{\overrightarrow {v}}_{2}}
v
→
1
{\displaystyle {\overrightarrow {v}}_{1}}
w
→
{\displaystyle {\overrightarrow {w}}}
v
→
2
{\displaystyle {\overrightarrow {v}}_{2}}
w
→
{\displaystyle {\overrightarrow {w}}}
v
→
⋅
w
→
=
2
⋅
4
+
(
−
1
)
⋅
(
−
1
)
+
3
⋅
2
=
8
+
1
+
6
=
15
{\displaystyle \qquad {\overrightarrow {v}}\cdot {\overrightarrow {w}}=2\cdot 4+(-1)\cdot (-1)+3\cdot 2=8+1+6=15}
|
w
→
|
2
=
4
2
+
(
−
1
)
2
+
2
2
=
16
+
1
+
4
=
21
{\displaystyle \qquad |{\overrightarrow {w}}|^{2}=4^{2}+(-1)^{2}+2^{2}=16+1+4=21}
v
→
1
=
p
r
o
j
w
→
v
→
=
(
v
→
.
w
→
|
w
→
|
2
)
.
w
→
=
(
15
21
)
.
(
4
,
−
1
,
2
)
=
(
60
21
,
−
15
21
,
30
21
)
=
(
20
7
,
−
5
7
,
10
7
)
{\displaystyle \qquad {\overrightarrow {v}}_{1}=proj_{\overrightarrow {w}}^{\overrightarrow {v}}=\left({\frac {{\overrightarrow {v}}.{\overrightarrow {w}}}{|{\overrightarrow {w}}|^{2}}}\right).{\overrightarrow {w}}=\left({\frac {15}{21}}\right).(4,-1,2)=\left({\frac {60}{21}},-{\frac {15}{21}},{\frac {30}{21}}\right)=\left({\frac {20}{7}},-{\frac {5}{7}},{\frac {10}{7}}\right)}
v
→
2
=
v
→
−
v
→
1
=
(
2
,
−
1
,
3
)
−
(
20
7
,
−
5
7
,
10
7
)
=
(
−
6
7
,
−
2
7
,
11
7
)
{\displaystyle \qquad {\overrightarrow {v}}_{2}={\overrightarrow {v}}-{\overrightarrow {v}}_{1}=(2,-1,3)-\left({\frac {20}{7}},-{\frac {5}{7}},{\frac {10}{7}}\right)=\left(-{\frac {6}{7}},-{\frac {2}{7}},{\frac {11}{7}}\right)}
Sejam
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
A norma de
v
→
×
w
→
{\displaystyle {\overrightarrow {v}}\times {\overrightarrow {w}}}
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
|
v
→
×
w
→
|
=
|
v
→
|
⋅
|
w
→
|
.
sen
θ
{\displaystyle \qquad \qquad |{\overrightarrow {v}}\times {\overrightarrow {w}}|=|{\overrightarrow {v}}|\cdot |{\overrightarrow {w}}|.\operatorname {sen} \theta }
Tem direção perpendicular a
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
Tem o sentido dado pela regra da mão direita. Se o ângulo entre
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
θ
{\displaystyle \theta }
v
→
{\displaystyle {\overrightarrow {v}}}
θ
{\displaystyle \theta }
w
→
{\displaystyle {\overrightarrow {w}}}
v
→
×
w
→
{\displaystyle {\overrightarrow {v}}\times {\overrightarrow {w}}}
Regra da mão direita Sejam
u
→
{\displaystyle {\overrightarrow {u}}}
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
α
{\displaystyle \alpha }
v
→
×
w
→
=
−
(
w
→
×
v
→
)
{\displaystyle {\overrightarrow {v}}\times {\overrightarrow {w}}=-({\overrightarrow {w}}\times {\overrightarrow {v}})}
{\displaystyle \qquad \qquad }
v
→
×
w
→
{\displaystyle {\overrightarrow {v}}\times {\overrightarrow {w}}}
w
→
×
v
→
{\displaystyle {\overrightarrow {w}}\times {\overrightarrow {v}}}
v
→
×
w
→
=
0
{\displaystyle {\overrightarrow {v}}\times {\overrightarrow {w}}=0}
v
→
=
α
w
→
{\displaystyle {\overrightarrow {v}}=\alpha {\overrightarrow {w}}}
w
→
=
α
v
→
{\displaystyle {\overrightarrow {w}}=\alpha {\overrightarrow {v}}}
{\displaystyle \qquad \qquad }
|
v
→
×
w
→
|
=
0
{\displaystyle |{\overrightarrow {v}}\times {\overrightarrow {w}}|=0}
sen
θ
=
0
{\displaystyle \operatorname {sen} \theta =0}
θ
{\displaystyle \theta }
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
(
v
→
×
w
→
)
⋅
v
→
=
(
v
→
×
w
→
)
⋅
w
→
=
0
{\displaystyle ({\overrightarrow {v}}\times {\overrightarrow {w}})\cdot {\overrightarrow {v}}=({\overrightarrow {v}}\times {\overrightarrow {w}})\cdot {\overrightarrow {w}}=0}
α
(
v
→
×
w
→
)
=
(
α
v
→
)
×
w
→
=
v
→
×
(
α
w
→
)
{\displaystyle \alpha ({\overrightarrow {v}}\times {\overrightarrow {w}})=(\alpha {\overrightarrow {v}})\times {\overrightarrow {w}}={\overrightarrow {v}}\times (\alpha {\overrightarrow {w}})}
v
→
×
(
w
→
+
u
→
)
=
v
→
×
w
→
+
v
→
×
u
→
{\displaystyle {\overrightarrow {v}}\times ({\overrightarrow {w}}+{\overrightarrow {u}})={\overrightarrow {v}}\times {\overrightarrow {w}}+{\overrightarrow {v}}\times {\overrightarrow {u}}}
(
v
→
+
w
→
)
×
u
→
=
v
→
×
u
→
+
w
→
×
u
→
{\displaystyle ({\overrightarrow {v}}+{\overrightarrow {w}})\times {\overrightarrow {u}}={\overrightarrow {v}}\times {\overrightarrow {u}}+{\overrightarrow {w}}\times {\overrightarrow {u}}}
{\displaystyle \quad }
Vetores unitários são vetores paralelos aos eixos coordenados, de norma igual a um.
Todo vetor
v
→
=
(
v
1
,
v
2
,
v
3
)
{\displaystyle {\overrightarrow {v}}=(v_{1},v_{2},v_{3})}
i
→
{\displaystyle {\overrightarrow {i}}}
j
→
{\displaystyle {\overrightarrow {j}}}
k
→
{\displaystyle {\overrightarrow {k}}}
v
→
=
(
v
1
,
v
2
,
v
3
)
=
(
v
1
,
0
,
0
)
+
(
0
,
v
2
,
0
)
+
(
0
,
0
,
v
3
)
=
v
1
(
1
,
0
,
0
)
+
v
2
(
0
,
1
,
0
)
+
v
3
(
0
,
0
,
1
)
=
v
1
i
→
+
v
2
j
→
+
v
3
k
→
{\displaystyle {\overrightarrow {v}}=(v_{1},v_{2},v_{3})=(v_{1},0,0)+(0,v_{2},0)+(0,0,v_{3})=v_{1}(1,0,0)+v_{2}(0,1,0)+v_{3}(0,0,1)=v_{1}{\overrightarrow {i}}+v_{2}{\overrightarrow {j}}+v_{3}{\overrightarrow {k}}}
Da definição do produto vetorial, obtêm-se as seguintes relações:
i
→
×
i
→
=
0
{\displaystyle \quad {\overrightarrow {i}}\times {\overrightarrow {i}}=0}
j
→
×
j
→
=
0
{\displaystyle \quad {\overrightarrow {j}}\times {\overrightarrow {j}}=0}
k
→
×
k
→
=
0
{\displaystyle \quad {\overrightarrow {k}}\times {\overrightarrow {k}}=0}
i
→
×
j
→
=
k
→
{\displaystyle \quad {\overrightarrow {i}}\times {\overrightarrow {j}}={\overrightarrow {k}}}
j
→
×
k
→
=
i
→
{\displaystyle \quad {\overrightarrow {j}}\times {\overrightarrow {k}}={\overrightarrow {i}}}
k
→
×
i
→
=
j
→
{\displaystyle \quad {\overrightarrow {k}}\times {\overrightarrow {i}}={\overrightarrow {j}}}
j
→
×
i
→
=
−
k
→
{\displaystyle \quad {\overrightarrow {j}}\times {\overrightarrow {i}}=-{\overrightarrow {k}}}
k
→
×
j
→
=
−
i
→
{\displaystyle \quad {\overrightarrow {k}}\times {\overrightarrow {j}}=-{\overrightarrow {i}}}
i
→
×
k
→
=
−
j
→
{\displaystyle \quad {\overrightarrow {i}}\times {\overrightarrow {k}}=-{\overrightarrow {j}}}
Sejam
v
→
=
(
v
1
,
v
2
,
v
3
)
{\displaystyle {\overrightarrow {v}}=(v_{1},v_{2},v_{3})}
w
→
=
(
w
1
,
w
2
,
w
3
)
{\displaystyle {\overrightarrow {w}}=(w_{1},w_{2},w_{3})}
produto vetorial
v
→
×
w
→
{\displaystyle {\overrightarrow {v}}\times {\overrightarrow {w}}}
v
→
×
w
→
=
[
i
j
k
u
1
u
2
u
3
v
1
v
2
v
3
]
{\displaystyle \qquad {\overrightarrow {v}}\times {\overrightarrow {w}}={\begin{bmatrix}i&j&k\\u_{1}&u_{2}&u_{3}\\v_{1}&v_{2}&v_{3}\end{bmatrix}}}
Demonstração:
v
→
=
v
1
i
→
+
v
2
j
→
+
v
3
k
→
{\displaystyle \qquad {\overrightarrow {v}}=v_{1}{\overrightarrow {i}}+v_{2}{\overrightarrow {j}}+v_{3}{\overrightarrow {k}}}
w
→
=
w
1
i
→
+
w
2
j
→
+
w
3
k
→
{\displaystyle {\overrightarrow {w}}=w_{1}{\overrightarrow {i}}+w_{2}{\overrightarrow {j}}+w_{3}{\overrightarrow {k}}}
v
→
×
w
→
=
(
v
1
i
→
+
v
2
j
→
+
v
3
k
→
)
×
(
w
1
i
→
+
w
2
j
→
+
w
3
k
→
)
{\displaystyle \qquad {\overrightarrow {v}}\times {\overrightarrow {w}}=(v_{1}{\overrightarrow {i}}+v_{2}{\overrightarrow {j}}+v_{3}{\overrightarrow {k}})\times (w_{1}{\overrightarrow {i}}+w_{2}{\overrightarrow {j}}+w_{3}{\overrightarrow {k}})}
=
v
1
w
1
(
i
→
×
i
→
)
+
v
1
w
2
(
i
→
×
j
→
)
+
v
1
w
3
(
i
→
×
k
→
)
+
v
2
w
1
(
j
→
×
i
→
)
+
v
2
w
2
(
j
→
×
j
→
)
+
v
2
w
3
(
j
→
×
k
→
)
+
v
3
w
1
(
k
→
×
i
→
)
+
v
3
w
2
(
k
→
×
j
→
)
+
v
3
w
3
(
k
→
×
k
→
)
{\displaystyle \qquad \qquad \quad =v_{1}w_{1}({\overrightarrow {i}}\times {\overrightarrow {i}})+v_{1}w_{2}({\overrightarrow {i}}\times {\overrightarrow {j}})+v_{1}w_{3}({\overrightarrow {i}}\times {\overrightarrow {k}})+v_{2}w_{1}({\overrightarrow {j}}\times {\overrightarrow {i}})+v_{2}w_{2}({\overrightarrow {j}}\times {\overrightarrow {j}})+v_{2}w_{3}({\overrightarrow {j}}\times {\overrightarrow {k}})+v_{3}w_{1}({\overrightarrow {k}}\times {\overrightarrow {i}})+v_{3}w_{2}({\overrightarrow {k}}\times {\overrightarrow {j}})+v_{3}w_{3}({\overrightarrow {k}}\times {\overrightarrow {k}})}
=
v
1
w
2
(
i
→
×
j
→
)
+
v
1
w
3
(
i
→
×
k
→
)
+
v
2
w
1
(
j
→
×
i
→
)
+
v
2
w
3
(
j
→
×
k
→
)
+
v
3
w
1
(
k
→
×
i
→
)
+
v
3
w
2
(
k
→
×
j
→
)
{\displaystyle \qquad \qquad \quad =v_{1}w_{2}({\overrightarrow {i}}\times {\overrightarrow {j}})+v_{1}w_{3}({\overrightarrow {i}}\times {\overrightarrow {k}})+v_{2}w_{1}({\overrightarrow {j}}\times {\overrightarrow {i}})+v_{2}w_{3}({\overrightarrow {j}}\times {\overrightarrow {k}})+v_{3}w_{1}({\overrightarrow {k}}\times {\overrightarrow {i}})+v_{3}w_{2}({\overrightarrow {k}}\times {\overrightarrow {j}})}
i
→
×
i
→
=
j
→
×
j
→
=
k
→
×
k
→
=
0
{\displaystyle {\overrightarrow {i}}\times {\overrightarrow {i}}={\overrightarrow {j}}\times {\overrightarrow {j}}={\overrightarrow {k}}\times {\overrightarrow {k}}=0}
=
(
v
1
w
2
)
k
→
+
(
v
1
w
3
)
(
−
j
→
)
+
(
v
2
w
1
)
(
−
k
→
)
+
(
v
2
w
3
)
i
→
+
(
v
3
w
1
)
j
→
+
(
v
3
w
2
)
(
−
i
→
)
{\displaystyle \qquad \qquad \quad =(v_{1}w_{2}){\overrightarrow {k}}+(v_{1}w_{3})(-{\overrightarrow {j}})+(v_{2}w_{1})(-{\overrightarrow {k}})+(v_{2}w_{3}){\overrightarrow {i}}+(v_{3}w_{1}){\overrightarrow {j}}+(v_{3}w_{2})(-{\overrightarrow {i}})}
=
(
v
2
w
3
−
v
3
w
2
)
i
→
+
(
v
3
w
1
−
v
1
w
3
)
j
→
+
(
v
1
w
2
−
v
2
w
1
)
k
→
{\displaystyle \qquad \qquad \quad =(v_{2}w_{3}-v_{3}w_{2}){\overrightarrow {i}}+(v_{3}w_{1}-v_{1}w_{3}){\overrightarrow {j}}+(v_{1}w_{2}-v_{2}w_{1}){\overrightarrow {k}}}
=
[
i
j
k
v
1
v
2
v
3
w
1
w
2
w
3
]
{\displaystyle \qquad \qquad \quad ={\begin{bmatrix}i&j&k\\v_{1}&v_{2}&v_{3}\\w_{1}&w_{2}&w_{3}\end{bmatrix}}}
Exemplo:
Sejam
v
→
=
i
→
+
2
j
→
−
2
k
→
{\displaystyle {\overrightarrow {v}}={\overrightarrow {i}}+2{\overrightarrow {j}}-2{\overrightarrow {k}}}
w
→
=
3
i
→
+
k
→
{\displaystyle {\overrightarrow {w}}=3{\overrightarrow {i}}+{\overrightarrow {k}}}
v
→
×
w
→
=
[
i
j
k
v
1
v
2
v
3
w
1
w
2
w
3
]
{\displaystyle \qquad {\overrightarrow {v}}\times {\overrightarrow {w}}={\begin{bmatrix}i&j&k\\v_{1}&v_{2}&v_{3}\\w_{1}&w_{2}&w_{3}\end{bmatrix}}}
=
[
i
j
k
1
2
−
2
3
0
1
]
{\displaystyle \qquad \qquad \quad ={\begin{bmatrix}i&j&k\\1&2&-2\\3&0&1\end{bmatrix}}}
=
(
2
−
0
)
i
→
+
(
−
6
−
1
)
j
→
+
(
0
−
6
)
k
→
{\displaystyle \qquad \qquad \quad =(2-0){\overrightarrow {i}}+(-6-1){\overrightarrow {j}}+(0-6){\overrightarrow {k}}}
=
2
i
→
−
7
j
→
−
6
k
→
=
(
2
,
−
7
,
−
6
)
{\displaystyle \qquad \qquad \quad =2{\overrightarrow {i}}-7{\overrightarrow {j}}-6{\overrightarrow {k}}=(2,-7,-6)}
O produto misto de
u
→
{\displaystyle {\overrightarrow {u}}}
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
u
→
⋅
(
v
→
×
w
→
)
{\displaystyle {\overrightarrow {u}}\cdot ({\overrightarrow {v}}\times {\overrightarrow {w}})}
Sejam
u
→
=
(
u
1
i
→
,
u
2
j
→
,
u
3
k
→
)
{\displaystyle {\overrightarrow {u}}=(u_{1}{\overrightarrow {i}},u_{2}{\overrightarrow {j}},u_{3}{\overrightarrow {k}})}
v
→
=
(
v
1
i
→
,
v
2
j
→
,
v
3
k
→
)
{\displaystyle {\overrightarrow {v}}=(v_{1}{\overrightarrow {i}},v_{2}{\overrightarrow {j}},v_{3}{\overrightarrow {k}})}
w
→
=
(
w
1
i
→
,
w
2
j
→
,
w
3
k
→
)
{\displaystyle {\overrightarrow {w}}=(w_{1}{\overrightarrow {i}},w_{2}{\overrightarrow {j}},w_{3}{\overrightarrow {k}})}
u
→
⋅
(
v
→
×
w
→
)
=
[
u
1
u
2
u
3
v
1
v
2
v
3
w
1
w
2
w
3
]
{\displaystyle \qquad {\overrightarrow {u}}\cdot ({\overrightarrow {v}}\times {\overrightarrow {w}})={\begin{bmatrix}u_{1}&u_{2}&u_{3}\\v_{1}&v_{2}&v_{3}\\w_{1}&w_{2}&w_{3}\end{bmatrix}}}
Exemplo:
O produto misto dos vetores
u
→
=
2
i
→
−
j
→
+
3
k
→
{\displaystyle {\overrightarrow {u}}=2{\overrightarrow {i}}-{\overrightarrow {j}}+3{\overrightarrow {k}}}
v
→
=
−
i
→
+
4
j
→
+
k
→
{\displaystyle {\overrightarrow {v}}=-{\overrightarrow {i}}+4{\overrightarrow {j}}+{\overrightarrow {k}}}
w
→
=
5
i
→
+
j
→
−
2
k
→
{\displaystyle {\overrightarrow {w}}=5{\overrightarrow {i}}+{\overrightarrow {j}}-2{\overrightarrow {k}}}
u
→
⋅
(
v
→
×
w
→
)
=
[
u
1
u
2
u
3
v
1
v
2
v
3
w
1
w
2
w
3
]
{\displaystyle \qquad {\overrightarrow {u}}\cdot ({\overrightarrow {v}}\times {\overrightarrow {w}})={\begin{bmatrix}u_{1}&u_{2}&u_{3}\\v_{1}&v_{2}&v_{3}\\w_{1}&w_{2}&w_{3}\end{bmatrix}}}
=
[
2
−
1
3
−
1
4
1
5
1
−
2
]
{\displaystyle \qquad \qquad \qquad \quad ={\begin{bmatrix}2&-1&3\\-1&4&1\\5&1&-2\end{bmatrix}}}
=
(
−
16
−
2
)
+
(
−
5
−
(
−
2
)
)
+
(
−
3
−
60
)
{\displaystyle \qquad \qquad \qquad \quad =(-16-2)+(-5-(-2))+(-3-60)}
=
−
18
−
3
−
63
=
−
84
{\displaystyle \qquad \qquad \qquad \quad =-18-3-63=-84}
{\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad }
Dados três vetores no espaço
u
→
{\displaystyle {\overrightarrow {u}}}
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
|
u
→
⋅
(
v
→
×
w
→
)
|
{\displaystyle |{\overrightarrow {u}}\cdot ({\overrightarrow {v}}\times {\overrightarrow {w}})|}
volume do paralelepípedo determinado por
u
→
{\displaystyle {\overrightarrow {u}}}
v
→
{\displaystyle {\overrightarrow {v}}}
w
→
{\displaystyle {\overrightarrow {w}}}
(colocar imagem)
Exemplo:
Sejam
u
→
=
3
i
→
+
3
j
→
+
4
k
→
{\displaystyle {\overrightarrow {u}}=3{\overrightarrow {i}}+3{\overrightarrow {j}}+4{\overrightarrow {k}}}
v
→
=
4
i
→
−
j
→
−
3
k
→
{\displaystyle {\overrightarrow {v}}=4{\overrightarrow {i}}-{\overrightarrow {j}}-3{\overrightarrow {k}}}
w
→
=
2
i
→
+
5
j
→
+
k
→
{\displaystyle {\overrightarrow {w}}=2{\overrightarrow {i}}+5{\overrightarrow {j}}+{\overrightarrow {k}}}
v
o
l
u
m
e
=
|
u
→
⋅
(
v
→
×
w
→
)
|
{\displaystyle \qquad volume=|{\overrightarrow {u}}\cdot ({\overrightarrow {v}}\times {\overrightarrow {w}})|}
=
‖
u
1
u
2
u
3
v
1
v
2
v
3
w
1
w
2
w
3
‖
{\displaystyle \qquad \qquad \quad ={\begin{Vmatrix}u_{1}&u_{2}&u_{3}\\v_{1}&v_{2}&v_{3}\\w_{1}&w_{2}&w_{3}\end{Vmatrix}}}
=
‖
3
3
4
4
−
1
−
3
2
5
1
‖
{\displaystyle \qquad \qquad \quad ={\begin{Vmatrix}3&3&4\\4&-1&-3\\2&5&1\end{Vmatrix}}}
=
|
(
−
3
−
(
−
45
)
)
+
(
−
18
−
12
)
+
(
80
−
(
−
8
)
)
|
{\displaystyle \qquad \qquad \quad =|(-3-(-45))+(-18-12)+(80-(-8))|}
=
|
42
−
30
+
88
|
{\displaystyle \qquad \qquad \quad =|42-30+88|}
=
|
100
|
=
100
{\displaystyle \qquad \qquad \quad =|100|=100}
{\displaystyle \quad }
------------Página Vetores--------------------
-------------Ângulos--------------
↑ a b c d e f g Ripoll, Cydara Cavedon (2011). Números Racionais, Reais e Complexos Ed. 2 . [S.l.]: UFRGS. ISBN 9788538601289 


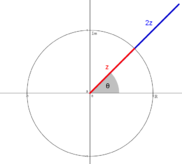










![{\displaystyle \mathbb {Z} =[...-3,-2,-1,1,2,3...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d384544f25d30df05034869bba59328a8732ac8)

![{\displaystyle =\mathbb {Z} -[0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c4c32812489d4f2e4d71fa424c6bc490ec1dbbd)

![{\displaystyle =[0,1,2,3...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c38c854524a2ac1ded987a3bbce4c1f8b65502fd)

![{\displaystyle =[1,2,3...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/396bb5485dbc1b722977211473b9284a9dab7645)
![{\displaystyle =[...-3,-2,-1,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4abcd4e73d351f6f226945afda8bb5480b0af26e)
![{\displaystyle =[...-3,-2,-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5566bb4b43657b58d72745c1b85913514b0f0f2)


![{\displaystyle [\mathbb {Z} ,+,\cdot ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8072714370978ff03dbdebd140e6df863f384916)



































































































































































































































































































































































































































































