Usuário(a):Wcris~ptwiki/quanta book

Predefinição:No footnotes Predefinição:Quantum In quantum mechanics, the EPR paradox (or Einstein–Podolsky–Rosen paradox) is a thought experiment which challenged long-held ideas about the relation between the observed values of physical quantities and the values that can be accounted for by a physical theory. "EPR" stands for Einstein, Podolsky, and Rosen, who introduced the thought experiment in a 1935 paper to argue that quantum mechanics is not a complete physical theory.

According to its authors the EPR experiment yields a dichotomy. Either

1. The result of a measurement performed on one part A of a quantum system has a non-local effect on the physical reality of another distant part B, in the sense that quantum mechanics can predict outcomes of some measurements carried out at B; or...
2. Quantum mechanics is incomplete in the sense that some element of physical reality corresponding to B cannot be accounted for by quantum mechanics (that is, some extra variable is needed to account for it.)

As it was shown later by Bell one cannot introduce the notion of "elements of reality" without affecting the predictions of the theory. That is, one cannot complete quantum mechanics with these "elements", because this automatically leads to some logical contradictions.

Einstein never accepted quantum mechanics as a "real" and complete theory, struggling to the end of his life for an interpretation that could comply with relativity without complying with the Heisenberg Uncertainty Principle. As he once said: "God does not play dice", skeptically referring to the Copenhagen Interpretation of quantum mechanics which says there exists no objective physical reality other than that which is revealed through measurement and observation.

The EPR paradox is a paradox in the following sense: if one adds to quantum mechanics some seemingly reasonable (but actually wrong, or questionable as a whole) conditions (referred to as locality) — realism (not to be confused with philosophical realism), counterfactual definiteness, and completeness (see Bell inequality and Bell test experiments) — then one obtains a contradiction. However, quantum mechanics by itself does not appear to be internally inconsistent, nor — as it turns out — does it contradict relativity. As a result of further theoretical and experimental developments since the original EPR paper, most physicists today regard the EPR paradox as an illustration of how quantum mechanics violates classical intuitions.

Quantum mechanics and its interpretation

During the twentieth century, quantum theory proved to be a successful theory, which describes the physical reality of the mesoscopic and microscopic world.

Quantum mechanics was developed with the aim of describing atoms and to explain the observed spectral lines in a measurement apparatus. The fact that quantum theory allows for an accurate description of reality is clear from many physical experiments and has probably never been seriously disputed. Interpretations of quantum phenomena are another story.

The question of how to interpret the mathematical formulation of quantum mechanics has given rise to a variety of different answers from people of different philosophical backgrounds.

Quantum theory and quantum mechanics do not account for single measurement outcomes in a deterministic way. According to an accepted interpretation of quantum mechanics known as the Copenhagen interpretation, a measurement causes an instantaneous collapse of the wave function describing the quantum system into an eigenstate of the observable that was measured.

The most prominent opponent of the Copenhagen interpretation was Albert Einstein. Einstein did not believe in the idea of genuine randomness in nature, the main argument in the Copenhagen interpretation. In his view, quantum mechanics is incomplete and suggests that there had to be 'hidden' variables responsible for random measurement results.

The famous paper "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?"[4], authored by Einstein, Podolsky and Rosen in 1935, condensed the philosophical discussion into a physical argument. They claim that given a specific experiment, in which the outcome of a measurement could be known before the measurement takes place, there must exist something in the real world, an "element of reality", which determines the measurement outcome. They postulate that these elements of reality are local, in the sense that they belong to a certain point in spacetime. This element may only be influenced by events which are located in the backward light cone of this point in spacetime. Even though these claims sound reasonable and convincing, they are founded on assumptions about nature which constitute what is now known as local realism.

Though the EPR paper has often been taken as an exact expression of Einstein's views, it was primarily authored by Podolsky, based on discussions at the Institute for Advanced Study with Einstein and Rosen. Einstein later expressed to Erwin Schrödinger that "It did not come out as well as I had originally wanted; rather, the essential thing was, so to speak, smothered by the formalism."

Description of the paradox

The EPR paradox draws on a phenomenon predicted by quantum mechanics, known as quantum entanglement, to show that measurements performed on spatially separated parts of a quantum system can apparently have an instantaneous influence on one another.

This effect is now known as "nonlocal behavior" (or colloquially as "quantum weirdness" or "spooky action at a distance").

Simple version

Before delving into the complicated logic that leads to the 'paradox', it is perhaps worth mentioning the simple version of the argument, as described by Greene and others, which Einstein used to show that 'hidden variables' must exist.

Two electrons are emitted from a source, by pion decay, so that their spins are opposite; one electron’s spin about any axis is the negative of the other's. Also, due to uncertainty, making a measurement of a particle’s spin about one axis disturbs the particle so you now can’t measure its spin about any other axis.

Now say you measure one electron’s spin about the x-axis. This automatically tells you the other electron’s spin about the x-axis. Since you’ve done the measurement without disturbing the other electron in any way, it can’t be that the other electron "only came to have that state when you measured it", because you didn’t measure it! It must have had that spin all along. Also (although you can’t actually do it now that you’ve disturbed the electron), you could have taken the measurement about any other axis. So it follows that the other electron also had a definite spin about any other axis – much more information than the particle is capable of holding, and a "hidden variable" according to EPR.

Measurements on an entangled state

We have a source that emits pairs of electrons, with one electron sent to destination A, where there is an observer named Alice, and another sent to destination B, where there is an observer named Bob. According to quantum mechanics, we can arrange our source so that each emitted electron pair occupies a quantum state called a spin singlet. This can be viewed as a quantum superposition of two states, which we call state I and state II. In state I, electron A has spin pointing upward along the z-axis (+z) and electron B has spin pointing downward along the z-axis (-z). In state II, electron A has spin -z and electron B has spin +z. Therefore, it is impossible to associate either electron in the spin singlet with a state of definite spin. The electrons are thus said to be entangled.

The EPR thought experiment, performed with electrons. A source (center) sends electrons toward two observers, Alice (left) and Bob (right), who can perform spin measurements.

Alice now measures the spin along the z-axis. She can obtain one of two possible outcomes: +z or -z. Suppose she gets +z. According to quantum mechanics, the quantum state of the system collapses into state I. (Different interpretations of quantum mechanics have different ways of saying this, but the basic result is the same.) The quantum state determines the probable outcomes of any measurement performed on the system. In this case, if Bob subsequently measures spin along the z-axis, he will obtain -z with 100% probability. Similarly, if Alice gets -z, Bob will get +z.

There is, of course, nothing special about our choice of the z-axis. For instance, suppose that Alice and Bob now decide to measure spin along the x-axis, according to quantum mechanics, the spin singlet state may equally well be expressed as a superposition of spin states pointing in the x direction. We'll call these states Ia and IIa. In state Ia, Alice's electron has spin +x and Bob's electron has spin -x. In state IIa, Alice's electron has spin -x and Bob's electron has spin +x. Therefore, if Alice measures +x, the system collapses into Ia, and Bob will get -x. If Alice measures -x, the system collapses into IIa, and Bob will get +x.

In quantum mechanics, the x-spin and z-spin are "incompatible observables", which means that there is a Heisenberg uncertainty principle operating between them: a quantum state cannot possess a definite value for both variables. Suppose Alice measures the z-spin and obtains +z, so that the quantum state collapses into state I. Now, instead of measuring the z-spin as well, Bob measures the x-spin. According to quantum mechanics, when the system is in state I, Bob's x-spin measurement will have a 50% probability of producing +x and a 50% probability of -x. Furthermore, it is fundamentally impossible to predict which outcome will appear until Bob actually performs the measurement.

Here is the crux of the matter. You might imagine that, when Bob measures the x-spin of his particle, he would get an answer with absolute certainty, since prior to this he hasn't disturbed his electron at all. But, as described above, Bob's electron has a 50% probability of producing +x and a 50% probability of -x - random behaviour, not certain. Bob's electron knows that Alice's electron has been measured, and its z-spin detected, and hence B's z-spin calculated, so its x-spin is 'out of bounds'.

Put another way, how does Bob's electron know, at the same time, which way to point if Alice decides (based on information unavailable to Bob) to measure x (i.e. be the opposite of Alice's electron's spin about the x-axis) and also how to point if Alice measures z (i.e. behave randomly), since it is only supposed to know one thing at a time? Using the usual Copenhagen interpretation rules that say the wave function "collapses" at the time of measurement, there must be action at a distance (entanglement) or the electron must know more than it is supposed to (hidden variables).

In case the explanation above is confusing, here is the paradox summed up;

Two electrons are emitted, shoot off and are measured later. Whatever axis their spins are measured along, they are always found to be opposite. This can only be explained if the electrons are linked in some way. Either they were created with a definite (opposite) spin about every axis - a "hidden variable" argument - or they are linked so that one electron knows what axis the other is having its spin measured along, and becomes its opposite about that one axis - an "entanglement" argument. Moreover, if the two electrons have their spins measured about different axes, once A's spin has been measured about the x-axis (and B's spin about the x-axis deduced), B's spin about the y-axis will no longer be certain, as if it knows that the measurement has taken place. Either that, or it has a definite spin already, which gives it a spin about a second axis - a hidden variable.

Incidentally, although we have used spin as an example, many types of physical quantities — what quantum mechanics refers to as "observables" — can be used to produce quantum entanglement. The original EPR paper used momentum for the observable. Experimental realizations of the EPR scenario often use photon polarization, because polarized photons are easy to prepare and measure.

Reality and completeness

We will now introduce two concepts used by Einstein, Podolsky, and Rosen (EPR), which are crucial to their attack on quantum mechanics: (i) the elements of physical reality and (ii) the completeness of a physical theory.

The authors (EPR) did not directly address the philosophical meaning of an "element of physical reality". Instead, they made the assumption that if the value of any physical quantity of a system can be predicted with absolute certainty prior to performing a measurement or otherwise disturbing it, then that quantity corresponds to an element of physical reality. Note that the converse is not assumed to be true; even if there are some "elements of physical reality" whose value cannot be predicted, this will not affect the argument.

Next, EPR defined a "complete physical theory" as one in which every element of physical reality is accounted for. The aim of their paper was to show, using these two definitions, that quantum mechanics is not a complete physical theory.

Let us see how these concepts apply to the above thought experiment. Suppose Alice decides to measure the value of spin along the z-axis (we'll call this the z-spin.) After Alice performs her measurement, the z-spin of Bob's electron is definitely known, so it is an element of physical reality. Similarly, if Bob decides to measure spin of his electron along the x-axis, the x-spin of Alice's electron becomes an element of physical reality after the measurement. After such measurements, the conclusion that Alice's and Bob's electrons now have definite values of spin along both the X and Z axis simultaneously is inevitable.

We have seen that a quantum state cannot possess a definite value for both x-spin and z-spin. If quantum mechanics is a complete physical theory in the sense given above, x-spin and z-spin cannot be elements of reality at the same time. This means that Alice's decision — whether to perform her measurement along the x- or z-axis — has an instantaneous effect on the elements of physical reality at Bob's location. However, this violates another principle, that of locality.

Locality in the EPR experiment

The principle of locality states that physical processes occurring at one place should have no immediate effect on the elements of reality at another location. At first sight, this appears to be a reasonable assumption to make, as it seems to be a consequence of special relativity, which states that information can never be transmitted faster than the speed of light without violating causality. It is generally believed that any theory which violates causality would also be internally inconsistent, and thus deeply unsatisfactory.

It turns out that the usual rules for combining quantum mechanical and classical descriptions violate the principle of locality without violating causality. Causality is preserved because there is no way for Alice to transmit messages (i.e. information) to Bob by manipulating her measurement axis. Whichever axis she uses, she has a 50% probability of obtaining "+" and 50% probability of obtaining "-", completely at random; according to quantum mechanics, it is fundamentally impossible for her to influence what result she gets. Furthermore, Bob is only able to perform his measurement once: there is a fundamental property of quantum mechanics, known as the "no cloning theorem", which makes it impossible for him to make a million copies of the electron he receives, perform a spin measurement on each, and look at the statistical distribution of the results. Therefore, in the one measurement he is allowed to make, there is a 50% probability of getting "+" and 50% of getting "-", regardless of whether or not his axis is aligned with Alice's.

However, the principle of locality appeals powerfully to physical intuition, and Einstein, Podolsky and Rosen were unwilling to abandon it. Einstein derided the quantum mechanical predictions as "spooky action at a distance". The conclusion they drew was that quantum mechanics is not a complete theory.

In recent years, however, doubt has been cast on EPR's conclusion due to developments in understanding locality and especially quantum decoherence. The word locality has several different meanings in physics. For example, in quantum field theory "locality" means that quantum fields at different points of space do not interact with one another. However, quantum field theories that are "local" in this sense appear to violate the principle of locality as defined by EPR, but they nevertheless do not violate locality in a more general sense. Wavefunction collapse can be viewed as an epiphenomenon of quantum decoherence, which in turn is nothing more than an effect of the underlying local time evolution of the wavefunction of a system and all of its environment. Since the underlying behaviour doesn't violate local causality, it follows that neither does the additional effect of wavefunction collapse, whether real or apparent. Therefore, as outlined in the example above, neither the EPR experiment nor any quantum experiment demonstrates that faster-than-light signaling is possible.

Resolving the paradox

Hidden variables

There are several ways to resolve the EPR paradox. The one suggested by EPR is that quantum mechanics, despite its success in a wide variety of experimental scenarios, is actually an incomplete theory. In other words, there is some yet undiscovered theory of nature to which quantum mechanics acts as a kind of statistical approximation (albeit an exceedingly successful one). Unlike quantum mechanics, the more complete theory contains variables corresponding to all the "elements of reality". There must be some unknown mechanism acting on these variables to give rise to the observed effects of "non-commuting quantum observables", i.e. the Heisenberg uncertainty principle. Such a theory is called a hidden variable theory.

To illustrate this idea, we can formulate a very simple hidden variable theory for the above thought experiment. One supposes that the quantum spin-singlet states emitted by the source are actually approximate descriptions for "true" physical states possessing definite values for the z-spin and x-spin. In these "true" states, the electron going to Bob always has spin values opposite to the electron going to Alice, but the values are otherwise completely random. For example, the first pair emitted by the source might be "(+z, -x) to Alice and (-z, +x) to Bob", the next pair "(-z, -x) to Alice and (+z, +x) to Bob", and so forth. Therefore, if Bob's measurement axis is aligned with Alice's, he will necessarily get the opposite of whatever Alice gets; otherwise, he will get "+" and "-" with equal probability.

Assuming we restrict our measurements to the z and x axes, such a hidden variable theory is experimentally indistinguishable from quantum mechanics. In reality, of course, there is an (uncountably) infinite number of axes along which Alice and Bob can perform their measurements, so there has to be an infinite number of independent hidden variables. However, this is not a serious problem; we have formulated a very simplistic hidden variable theory, and a more sophisticated theory might be able to patch it up. It turns out that there is a much more serious challenge to the idea of hidden variables.

Bell's inequality

Ver artigo principal: Bell's theorem

In 1964, John Bell showed that the predictions of quantum mechanics in the EPR thought experiment are significantly different from the predictions of a very broad class of hidden variable theories (the local hidden variable theories). Roughly speaking, quantum mechanics predicts much stronger statistical correlations between the measurement results performed on different axes than the hidden variable theories. These differences, expressed using inequality relations known as "Bell's inequalities", are in principle experimentally detectable. Later work by Eberhard showed that the key properties of local hidden variable theories that lead to Bell's inequalities are locality and counter-factual definiteness. Any theory in which these principles hold produces the inequalities. A. Fine subsequently showed that any theory satisfying the inequalities can be modeled by a local hidden variable theory.

After the publication of Bell's paper, a variety of experiments were devised to test Bell's inequalities. (As mentioned above, these experiments generally rely on photon polarization measurements.) All the experiments conducted to date have found behavior in line with the predictions of standard quantum mechanics.

However, Bell's theorem does not apply to all possible philosophically realist theories, although a common misconception touted by new agers is that quantum mechanics is inconsistent with all notions of philosophical realism. Realist interpretations of quantum mechanics are possible, although as discussed above, such interpretations must reject either locality or counter-factual definiteness. Mainstream physics prefers to keep locality while still maintaining a notion of realism that nevertheless rejects counter-factual definiteness. Examples of such mainstream realist interpretations are the consistent histories interpretation and the transactional interpretation. Fine's work showed that taking locality as a given there exist scenarios in which two statistical variables are correlated in a manner inconsistent with counter-factual definiteness and that such scenarios are no more mysterious than any other despite the inconsistency with counter-factual definiteness seeming 'counter-intuitive'. Violation of locality however is difficult to reconcile with special relativity and is thought to be incompatible with the principle of causality. On the other hand the Bohm interpretation of quantum mechanics instead keeps counter-factual definiteness while introducing a conjectured non-local mechanism called the 'quantum potential'. Some workers in the field have also attempted to formulate hidden variable theories that exploit loopholes in actual experiments, such as the assumptions made in interpreting experimental data although no such theory has been produced that can reproduce all the results of quantum mechanics.

There are also individual EPR-like experiments that have no local hidden variables explanation. Examples have been suggested by David Bohm and by Lucien Hardy.

"Acceptable theories", and the experiment

According to the present view of the situation, quantum mechanics simply contradicts Einstein's philosophical postulate that any acceptable physical theory should fulfill "local realism".

In the EPR paper (1935) the authors realized that quantum mechanics was non-acceptable in the sense of their above-mentioned assumptions, and Einstein thought erroneously that it could simply be augmented by 'hidden variables', without any further change, to get an acceptable theory. He pursued these ideas until the end of his life (1955), i.e. over twenty years.

In contrast, John Bell, in his 1964 paper, showed "once and for all" that quantum mechanics and Einstein's assumptions lead to different results, different by a factor of ${\frac {3}{2}}$, for certain correlations. So the issue of "acceptability", up to this time mainly concerning theory (even philosophy), finally became experimentally decidable.

There are many Bell test experiments hitherto, e.g. those of Alain Aspect and others. They all show that pure quantum mechanics, and not Einstein's "local realism", is acceptable. Thus, according to Karl Popper these experiments falsify Einstein's philosophical assumptions, especially the ideas on "hidden variables", whereas quantum mechanics itself remains a good candidate for a theory, which is acceptable in a wider context.

But apparently an experiment, which would also classify Bohm's non-local quasi-classical theory as non-acceptable, is still lacking.

Implications for quantum mechanics

Most physicists today believe that quantum mechanics is correct, and that the EPR paradox is a "paradox" only because classical intuitions do not correspond to physical reality. How EPR is interpreted regarding locality depends on the interpretation of quantum mechanics one uses. In the Copenhagen interpretation, it is usually understood that instantaneous wavefunction collapse does occur. However, the view that there is no causal instantaneous effect has also been proposed within the Copenhagen interpretation: in this alternate view, measurement affects our ability to define (and measure) quantities in the physical system, not the system itself. In the many-worlds interpretation, a kind of locality is preserved, since the effects of irreversible operations such as measurement arise from the relativization of a global state to a subsystem such as that of an observer.

The EPR paradox has deepened our understanding of quantum mechanics by exposing the fundamentally non-classical characteristics of the measurement process. Prior to the publication of the EPR paper, a measurement was often visualized as a physical disturbance inflicted directly upon the measured system. For instance, when measuring the position of an electron, one imagines shining a light on it, thus disturbing the electron and producing the quantum mechanical uncertainties in its position. Such explanations, which are still encountered in popular expositions of quantum mechanics, are debunked by the EPR paradox, which shows that a "measurement" can be performed on a particle without disturbing it directly, by performing a measurement on a distant entangled particle.

Technologies relying on quantum entanglement are now being developed. In quantum cryptography, entangled particles are used to transmit signals that cannot be eavesdropped upon without leaving a trace. In quantum computation, entangled quantum states are used to perform computations in parallel, which may allow certain calculations to be performed much more quickly than they ever could be with classical computers.

Mathematical formulation

The above discussion can be expressed mathematically using the quantum mechanical formulation of spin. The spin degree of freedom for an electron is associated with a two-dimensional Hilbert space H, with each quantum state corresponding to a vector in that space. The operators corresponding to the spin along the x, y, and z direction, denoted S_x, S_y, and S_z respectively, can be represented using the Pauli matrices:

$S_{x}={\frac {\hbar }{2}}{\begin{bmatrix}0&1\\1&0\end{bmatrix}},\quad S_{y}={\frac {\hbar }{2}}{\begin{bmatrix}0&-i\\i&0\end{bmatrix}},\quad S_{z}={\frac {\hbar }{2}}{\begin{bmatrix}1&0\\0&-1\end{bmatrix}}$

where $\hbar$ stands for Planck's constant divided by 2π.

The eigenstates of S_z are represented as

$\left|+z\right\rangle \leftrightarrow {\begin{bmatrix}1\\0\end{bmatrix}},\quad \left|-z\right\rangle \leftrightarrow {\begin{bmatrix}0\\1\end{bmatrix}}$

With qubits it looks:

$|0\rangle ={\begin{bmatrix}1\\0\end{bmatrix}},\quad |1\rangle ={\begin{bmatrix}0\\1\end{bmatrix}}$

and the eigenstates of S_x are represented as

$\left|+x\right\rangle \leftrightarrow {\frac {1}{\sqrt {2}}}{\begin{bmatrix}1\\1\end{bmatrix}},\quad \left|-x\right\rangle \leftrightarrow {\frac {1}{\sqrt {2}}}{\begin{bmatrix}1\\-1\end{bmatrix}}$

With qubits it looks:

$|+\rangle ={1 \over {\sqrt {2}}}(|0\rangle +|1\rangle )={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1\\1\end{bmatrix}},\quad |-\rangle ={1 \over {\sqrt {2}}}(|0\rangle -|1\rangle )={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1\\-1\end{bmatrix}}$

The Hilbert space of the electron pair is $H\otimes H$, the tensor product of the two electrons' Hilbert spaces. The spin singlet state is

$\left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|+z\right\rangle \otimes \left|-z\right\rangle -\left|-z\right\rangle \otimes \left|+z\right\rangle {\bigg )}$

With qubits it looks:

$|\psi \rangle ={\frac {1}{\sqrt {2}}}(|01\rangle -|10\rangle )$

where the two terms on the right hand side are what we have referred to as state I and state II above. This is also commonly written as

$\left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|+-\right\rangle -\left|-+\right\rangle {\bigg )}$

With qubits it looks:

$\left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|+-\right\rangle -\left|-+\right\rangle {\bigg )}={\frac {1}{\sqrt {2}}}{\bigg (}{1 \over {\sqrt {2}}}(|0\rangle +|1\rangle ){1 \over {\sqrt {2}}}(|0\rangle -|1\rangle )-{1 \over 2}(|0\rangle -|1\rangle )(|0\rangle +|1\rangle ){\bigg )}=$

$={\frac {1}{\sqrt {2}}}({1 \over 2}(|00\rangle -|01\rangle +|10\rangle -|11\rangle )-{1 \over 2}(|00\rangle +|01\rangle -|10\rangle -|11\rangle ))={\frac {1}{\sqrt {2}}}(|10\rangle -|01\rangle )$

From the above equations, it can be shown that the spin singlet can also be written as

$\left|\psi \right\rangle ={\frac {-1}{\sqrt {2}}}{\bigg (}\left|+x\right\rangle \otimes \left|-x\right\rangle -\left|-x\right\rangle \otimes \left|+x\right\rangle {\bigg )}$

With qubits it looks:

$|\psi \rangle =-{\frac {1}{\sqrt {2}}}{\bigg (}\left|+\right\rangle \otimes \left|-\right\rangle -\left|-\right\rangle \otimes \left|+\right\rangle {\bigg )}={\frac {-1}{\sqrt {2}}}(|10\rangle -|01\rangle )={\frac {1}{\sqrt {2}}}(|01\rangle -|10\rangle )$

where the terms on the right hand side are what we have referred to as state Ia and state IIa.

To illustrate how this leads to the violation of local realism, we need to show that after Alice's measurement of S_z (or S_x), Bob's value of S_z (or S_x) is uniquely determined, and therefore corresponds to an "element of physical reality". This follows from the principles of measurement in quantum mechanics. When S_z is measured, the system state ψ collapses into an eigenvector of S_z. If the measurement result is +z, this means that immediately after measurement the system state undergoes an orthogonal projection of ψ onto the space of states of the form

$\left|+z\right\rangle \otimes \left|\phi \right\rangle \quad \phi \in H$

With qubits it looks:

$\left|0\right\rangle \otimes \left|\phi \right\rangle \quad \phi \in H$

For the spin singlet, the new state is

$\left|+z\right\rangle \otimes \left|-z\right\rangle .$

With qubits it looks:

$\left|0\right\rangle \otimes \left|1\right\rangle .$

Similarly, if Alice's measurement result is -z, a system undergoes an orthogonal projection onto

$\left|-z\right\rangle \otimes \left|\phi \right\rangle \quad \phi \in H$

With qubits it looks:

$\left|1\right\rangle \otimes \left|\phi \right\rangle \quad \phi \in H$

which means that the new state is

$\left|-z\right\rangle \otimes \left|+z\right\rangle$

With qubits it looks:

$\left|1\right\rangle \otimes \left|0\right\rangle$

This implies that the measurement for S_z for Bob's electron is now determined. It will be -z in the first case or +z in the second case.

It remains only to show that S_x and S_z cannot simultaneously possess definite values in quantum mechanics. One may show in a straightforward manner that no possible vector can be an eigenvector of both matrices. More generally, one may use the fact that the operators do not commute,

$\left[S_{x},S_{z}\right]=-i\hbar S_{y}\neq 0$

along with the Heisenberg uncertainty relation

$\langle (\Delta S_{x})^{2}\rangle \langle (\Delta S_{z})^{2}\rangle \geq {\frac {1}{4}}\left|\langle \left[S_{x},S_{z}\right]\rangle \right|^{2}$

See also

• Bell test experiments
• Bell state
• Bell's theorem
• CHSH Bell test
• Coherence (physics)
• Counter-factual definiteness
• Ghirardi-Rimini-Weber theory
• GHZ experiment
• Interpretation of quantum mechanics
• Local hidden variable theory
• Many-worlds interpretation
• Measurement in quantum mechanics
• Measurement problem
• Penrose interpretation

• Philosophy of information
• Philosophy of physics
• Pondicherry interpretation
• Popper's experiment
• Quantum decoherence
• Quantum entanglement
• Quantum gravity
• Quantum information
• Quantum pseudo-telepathy
• Quantum teleportation
• Quantum Zeno effect
• Sakurai's Bell inequality
• Synchronicity
• Wave function collapse
• Zero-point field

References

Selected papers

• A. Aspect, Bell's inequality test: more ideal than ever, Nature 398 189 (1999). [5]
• J.S. Bell, On the Einstein-Poldolsky-Rosen paradox, Physics 1 195bbcv://prola.aps.org/abstract/PR/v48/i8/p696_1]
• P.H. Eberhard, Bell's theorem without hidden variables. Nuovo Cimento 38B1 75 (1977).
• P.H. Eberhard, Bell's theorem and the different concepts of locality. Nuovo Cimento 46B 392 (1978).
• A. Einstein, B. Podolsky, and N. Rosen, Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47 777 (1935). [6]

• A. Fine, Hidden Variables, Joint Probability, and the Bell Inequalities. Phys. Rev. Lett. 48, 291 (1982).[7]
• A. Fine, Do Correlations need to be explained?, in Philosophical Consequences of Quantum Theory: Reflections on Bell's Theorem, edited by Cushing & McMullin (University of Notre Dame Press, 1986).
• L. Hardy, Nonlocality for two particles without inequalities for almost all entangled states. Phys. Rev. Lett. 71 1665 (1993).[8]
• M. Mizuki, A classical interpretation of Bell's inequality. Annales de la Fondation Louis de Broglie 26 683 (2001).
• P. Pluch, "Theory for Quantum Probability", PhD Thesis University of Klagenfurt (2006)
• M. A. Rowe, D. Kielpinski, V. Meyer, C. A. Sackett, W. M. Itano, C. Monroe and D. J. Wineland, Experimental violation of a Bell's inequality with efficient detection, Nature 409, 791-794 (15 February 2001). [9]
• M. Smerlak, C. Rovelli, Relational EPR [10]

Books

• J.S. Bell, Speakable and Unspeakable in Quantum Mechanics (Cambridge University Press, 1987). ISBN 0-521-36869-3
• J.J. Sakurai, Modern Quantum Mechanics (Addison-Wesley, 1994), pp. 174–187, 223-232. ISBN 0-201-53929-2
• F. Selleri, Quantum Mechanics Versus Local Realism: The Einstein-Podolsky-Rosen Paradox (Plenum Press, New York, 1988). ISBN 0-306-42739-7
• Roger Penrose, The Road to Reality (Alfred A. Knopf, 2005; Vintage Books, 2006). ISBN 0-679-45443-8

External links

• The original EPR paper
• A. Fine, The Einstein-Podolsky-Rosen Argument in Quantum Theory
• Abner Shimony, Bell’s Theorem (2004)
• EPR, Bell & Aspect: The Original References
• Does Bell's Inequality Principle rule out local theories of quantum mechanics? From the Usenet Physics FAQ.
• Theoretical use of EPR in teleportation
• Effective use of EPR in cryptography

Category:Fundamental physics concepts Category:Physical paradoxes Category:Thought experiments Category:Quantum measurement Category:Albert Einstein Category:Articles with Alice and Bob explanations pt:Paradoxo EPR

Predefinição:Quantum mechanics Quantum entanglement is a possible property of a quantum mechanical state of a system of two or more objects in which the quantum states of the constituting objects are linked together so that one object can no longer be adequately described without full mention of its counterpart — even though the individual objects may be spatially separated. This interconnection leads to non-classical correlations between observable physical properties of remote systems, often referred to as nonlocal correlations.

For example, quantum mechanics holds that observables such as spin are indeterminate until such time as some physical intervention is made to measure the spin of the object in question. In the singlet state of two spins it is equally likely that any given particle will be observed to be spin-up as that it will be spin-down. Measuring any number of particles will result in an unpredictable series of measures that will tend more and more closely to half up and half down. However, if this experiment is done with entangled particles the results are quite different. When two members of an entangled pair are measured, one will always be spin-up and the other will be spin-down.{{carece de fontes}} The distance between the two particles is irrelevant.

Theories involving 'hidden variables' have been proposed in order to explain this result; these hidden variables account for the spin of each particle, and are determined when the entangled pair is created. It may appear then that the hidden variables must be in communication no matter how far apart the particles are, that the hidden variable describing one particle must be able to change instantly when the other is measured. If the hidden variables stop interacting when they are far apart, the statistics of multiple measurements must obey an inequality (called Bell's inequality), which is, however, violated — both by quantum mechanical theory and in experiments.{{carece de fontes}}

When pairs of particles are generated by the decay of other particles, naturally or through induced collision, these pairs may be termed "entangled", in that such pairs often necessarily have linked and opposite qualities, i.e. of spin or charge. The assumption that measurement in effect "creates" the state of the measured quality goes back to the arguments of, among others: Schrödinger, and Einstein, Podolsky, and Rosen{{carece de fontes}} (see EPR paradox) concerning Heisenberg's uncertainty principle and its relation to observation (see also the Copenhagen interpretation). The analysis of entangled particles by means of Bell's theorem, can lead to an impression of non-locality (that is, that there exists a connection between the members of such a pair that defies both classical and relativistic concepts of space and time). This is reasonable if it is assumed that each particle departs the scene of the pair's creation in an ambiguous state (as per a possible interpretation of Heisenberg). In such case, either dichotomous outcome of a given measurement remains a possibility; only measurement itself would precipitate a distinct value. On the other hand, if each particle departs the scene of its "entangled creation" with properties that would unambiguously determine the value of the quality to be subsequently measured, then a postulated instantaneous transmission of information across space and time would not be required to account for the result. The Bohm interpretation postulates that a guide wave exists connecting what are perceived as individual particles such that the supposed hidden variables are actually the particles themselves existing as functions of that wave.

Observation of wavefunction collapse can lead to the impression that measurements performed on one system instantaneously influence other systems entangled with the measured system, even when far apart. Yet another interpretation of this phenomenon is that quantum entanglement does not necessarily enable the transmission of classical information faster than the speed of light because a classical information channel is required to complete the process.{{carece de fontes}}

Background

Entanglement is one of the properties of quantum mechanics that caused Einstein and others to dislike the theory. In 1935, Einstein, Podolsky, and Rosen formulated the EPR paradox, a quantum-mechanical thought experiment with a highly counterintuitive and apparently nonlocal outcome, in response to Niels Bohr's advocacy of the belief that quantum mechanics as a theory was complete. Einstein famously derided entanglement as "spukhafte Fernwirkung"{{carece de fontes}} or "spooky action at a distance". It was his belief that future mathematicians would discover that quantum entanglement entailed nothing more or less than an error in their calculations. As he once wrote: "I find the idea quite intolerable that an electron exposed to radiation should choose of its own free will, not only its moment to jump off, but also its direction. In that case, I would rather be a cobbler, or even an employee in a gaming house, than a physicist".

On the other hand, quantum mechanics has been highly successful in producing correct experimental predictions, and the strong correlations predicted by the theory of quantum entanglement have now in fact been observed.{{carece de fontes}} One apparent way to explain found correlations in line with the predictions of quantum entanglement is an approach known as "local hidden variable theory", in which unknown, shared, local parameters would cause the correlations. However, in 1964 John Stewart Bell derived an upper limit, known as Bell's inequality, on the strength of correlations for any theory obeying "local realism". Quantum entanglement can lead to stronger correlations that violate this limit, so that quantum entanglement is experimentally distinguishable from a broad class of local hidden-variable theories.{{carece de fontes}} Results of subsequent experiments have overwhelmingly supported quantum mechanics. However, there may be experimental problems, known as "loopholes", that affect the validity of these experimental findings. High-efficiency and high-visibility experiments are now in progressPredefinição:Specify that should confirm or invalidate the existence of those loopholes. For more information, see the article on experimental tests of Bell's inequality.

Observations pertaining to entangled states appear to conflict with the property of relativity that information cannot be transferred faster than the speed of light. Although two entangled systems appear to interact across large spatial separations, the current state of belief is that no useful information can be transmitted in this way, meaning that causality cannot be violated through entanglement. This is the statement of the no-communication theorem.

Even if information cannot be transmitted through entanglement alone, it is believed that it is possible to transmit information using a set of entangled states used in conjunction with a classical information channel. This process is known as quantum teleportation. Despite its name, quantum teleportation may still not permit information to be transmitted faster than light, because a classical information channel is required to complete the process.

In addition experiments are underway to see if entanglement is the result of retrocausality.

Pure states

Predefinição:Tooabstract The following discussion builds on the theoretical framework developed in the articles bra-ket notation and mathematical formulation of quantum mechanics.{{carece de fontes}}

Consider two noninteracting systems $A$ and $B$, with respective Hilbert spaces $H_{A}$ and $H_{B}$. The Hilbert space of the composite system is the tensor product

$H_{A}\otimes H_{B}.$

If the first system is in state $|\scriptstyle \psi \rangle _{A}$ and the second in state $|\scriptstyle \phi \rangle _{B}$, the state of the composite system is

$|\psi \rangle _{A}\otimes |\phi \rangle _{B}.$

States of the composite system which can be represented in this form are called separable states, or product states.

Not all states are product states. Fix a basis $\scriptstyle \{|i\rangle _{A}\}$ for $H_{A}$ and a basis $\scriptstyle \{|j\rangle _{B}\}$ for $H_{B}$. The most general state in $\scriptstyle H_{A}\otimes H_{B}$ is of the form

$|\psi \rangle _{AB}=\sum _{i,j}c_{ij}|i\rangle _{A}\otimes |j\rangle _{B}$.

This state is separable if $\scriptstyle c_{ij}=c_{i}^{A}c_{j}^{B},$ yielding $\scriptstyle |\psi \rangle _{A}=\sum _{i}c_{i}^{A}|i\rangle _{A}$ and $\scriptstyle |\phi \rangle _{B}=\sum _{j}c_{j}^{B}|j\rangle _{B}.$ It is inseparable if $\scriptstyle c_{ij}\neq c_{i}^{A}c_{j}^{B}.$ If a state is inseparable, it is called an entangled state.

For example, given two basis vectors $\scriptstyle \{|0\rangle _{A},|1\rangle _{A}\}$ of $H_{A}$ and two basis vectors $\scriptstyle \{|0\rangle _{B},|1\rangle _{B}\}$ of $H_{B}$, the following is an entangled state:

${1 \over {\sqrt {2}}}{\bigg (}|0\rangle _{A}\otimes |1\rangle _{B}-|1\rangle _{A}\otimes |0\rangle _{B}{\bigg )}$.

If the composite system is in this state, it is impossible to attribute to either system $A$ or system $B$ a definite pure state. Instead, their states are superposed with one another. In this sense, the systems are "entangled".

Now suppose Alice is an observer for system $A$, and Bob is an observer for system $B$. If Alice makes a measurement in the $\scriptstyle \{|0\rangle ,|1\rangle \}$ eigenbasis of A, there are two possible outcomes, occurring with equal probability:{{carece de fontes}}

1. Alice measures 0, and the state of the system collapses to $\scriptstyle |0\rangle _{A}|1\rangle _{B}$.
2. Alice measures 1, and the state of the system collapses to $\scriptstyle |1\rangle _{A}|0\rangle _{B}$.

If the former occurs, then any subsequent measurement performed by Bob, in the same basis, will always return 1. If the latter occurs, (Alice measures 1) then Bob's measurement will return 0 with certainty. Thus, system B has been altered by Alice performing a local measurement on system A. This remains true even if the systems A and B are spatially separated. This is the foundation of the EPR paradox.

The outcome of Alice's measurement is random. Alice cannot decide which state to collapse the composite system into, and therefore cannot transmit information to Bob by acting on her system. Causality is thus preserved, in this particular scheme. For the general argument, see no-communication theorem.

In some formal mathematical settingsPredefinição:Specify, it is noted that the correct setting for pure states in quantum mechanics is projective Hilbert space endowed with the Fubini-Study metric. The product of two pure states is then given by the Segre embedding.

Ensembles

As mentioned above, a state of a quantum system is given by a unit vector in a Hilbert space. More generally, if one has a large number of copies of the same system, then the state of this ensemble is described by a density matrix, which is a positive matrix, or a trace class when the state space is infinite dimensional, and has trace 1. Again, by the spectral theorem, such a matrix takes the general form:

$\rho =\sum _{i}w_{i}|\alpha _{i}\rangle \langle \alpha _{i}|,$

where the $w_{i}$'s sum up to 1, and in the infinite dimensional case, we would take the closure of such states in the trace norm. We can interpret $\rho$ as representing an ensemble where $w_{i}$ is the proportion of the ensemble whose states are $|\alpha _{i}\rangle$. When a mixed state has rank 1, it therefore describes a pure ensemble. When there is less than total information about the state of a quantum system we need density matrices to represent the state.

Following the definition in previous section, for a bipartite composite system, mixed states are just density matrices on $H_{A}\otimes H_{B}$. Extending the definition of separability from the pure case, we say that a mixed state is separable if it can be written as

$\rho =\sum _{i}p_{i}\rho _{i}^{A}\otimes \rho _{i}^{B},$

where $\rho _{i}^{A}$'s and $\rho _{i}^{B}$'s are they themselves states on the subsystems A and B respectively. In other words, a state is separable if it is probability distribution over uncorrelated states, or product states. We can assume without loss of generality that $\rho _{i}^{A}$ and $\rho _{i}^{B}$ are pure ensembles. A state is then said to be entangled if it is not separable. In general, finding out whether or not a mixed state is entangled is considered difficult. Formally, it has been shown to be NP-hard. For the $2\times 2$ and $2\times 3$ cases, a necessary and sufficient criterion for separability is given by the famous Positive Partial Transpose (PPT) condition.

Experimentally, a mixed ensemble might be realized as follows. Consider a "black-box" apparatus that spits electrons towards an observer. The electrons' Hilbert spaces are identical. The apparatus might produce electrons that are all in the same state; in this case, the electrons received by the observer are then a pure ensemble. However, the apparatus could produce electrons in different states. For example, it could produce two populations of electrons: one with state $|\mathbf {z} +\rangle$ with spins aligned in the positive $\mathbf {z}$ direction, and the other with state $|\mathbf {y} -\rangle$ with spins aligned in the negative $\mathbf {y}$ direction. Generally, this is a mixed ensemble, as there can be any number of populations, each corresponding to a different state.

Reduced density matrices

Consider as above systems $A$ and $B$ each with a Hilbert space $H_{A}$, $H_{B}$. Let the state of the composite system be

$|\Psi \rangle \in H_{A}\otimes H_{B}.$

As indicated above, in general there is no way to associate a pure state to the component system $A$. However, it still is possible to associate a density matrix. Let

$\rho _{T}=|\Psi \rangle \;\langle \Psi |$.

which is the projection operator onto this state. The state of $A$ is the partial trace of $\rho _{T}$ over the basis of system $B$:

$\rho _{A}\ {\stackrel {\mathrm {def} }{=}}\ \sum _{j}\langle j|_{B}\left(|\Psi \rangle \langle \Psi |\right)|j\rangle _{B}={\hbox{Tr}}_{B}\;\rho _{T}$.

$\rho _{A}$ is sometimes called the reduced density matrix of $\rho$ on subsystem A. Colloquially, we "trace out" system B to obtain the reduced density matrix on A.

For example, the density matrix of $A$ for the entangled state discussed above is

$\rho _{A}=(1/2){\bigg (}|0\rangle _{A}\langle 0|_{A}+|1\rangle _{A}\langle 1|_{A}{\bigg )}$

This demonstrates that, as expected, the reduced density matrix for an entangled pure ensemble is a mixed ensemble. Also not surprisingly, the density matrix of $A$ for the pure product state $|\psi \rangle _{A}\otimes |\phi \rangle _{B}$ discussed above is

$\rho _{A}=|\psi \rangle _{A}\langle \psi |_{A}.$

In general, a bipartite pure state ρ is entangled if and only if one, meaning both, of its reduced states are mixed states.

Entropy

In this section we briefly discuss entropy of a mixed state and how it can be viewed as a measure of entanglement.

Definition

In classical information theory, to a probability distribution $p_{1},\cdots ,p_{n}$, one can associate the Shannon entropy:{{carece de fontes}}

$H(p_{1},\cdots ,p_{n})=-\sum _{i}p_{i}\log _{2}p_{i},$

Since a mixed state ρ is a probability distribution over an ensemble, this leads naturally to the definition of the von Neumann entropy:

$S(\rho )=-{\hbox{Tr}}\left(\rho \log {\rho }\right),$

where the logarithm is again taken in base 2. In general, to calculate $\;\log \rho$, one would use the Borel functional calculus. If ρ acts on a finite dimensional Hilbert space and has eigenvalues $\lambda _{1},\cdots ,\lambda _{n}$, then we recover the Shannon entropy:

$S(\rho )=-{\hbox{Tr}}\left(\rho \log {\rho }\right)=-\sum _{i}\lambda _{i}\log \lambda _{i}$.

Since an event of probability 0 should not contribute to the entropy, we adopt the convention that $0\log 0\;=0$. This extends to the infinite dimensional case as well: if ρ has spectral resolution $\rho =\int \lambda dP_{\lambda }$, then we assume the same convention when calculating

$\rho \log \rho =\int \lambda \log \lambda dP_{\lambda }.$

As in statistical mechanics, one can say that the more uncertainty (number of microstates) the system should possess, the larger the entropy. For example, the entropy of any pure state is zero, which is unsurprising since there is no uncertainty about a system in a pure state. The entropy of any of the two subsystems of the entangled state discussed above is $\log 2$ (which can be shown to be the maximum entropy for $2\times 2$ mixed states).

As a measure of entanglement

Entropy provides one tool which can be used to quantify entanglement, although other entanglement measures exist.{{carece de fontes}} If the overall system is pure, the entropy of one subsystem can be used to measure its degree of entanglement with the other subsystems.

For bipartite pure states, the von Neumann entropy of reduced states is the unique measure of entanglement in the sense that it is the only function on the family of states that satisfies certain axioms required of an entanglement measure.

It is a classical result that the Shannon entropy achieves its maximum at, and only at, the uniform probability distribution {1/n,...,1/n}. Therefore, a bipartite pure state

$\rho \in H\otimes H$

is said to be a maximally entangled state if there exists some local bases on H such that the reduced state of ρ is the diagonal matrix

${\begin{bmatrix}{\frac {1}{n}}&\;&\;\\\;&\ddots &\;\\\;&\;&{\frac {1}{n}}\end{bmatrix}}.$

For mixed states, the reduced von Neumann entropy is not the unique entanglement measure.

As an aside, the information-theoretic definition is closely related to entropy in the sense of statistical mechanics{{carece de fontes}} (comparing the two definitions, we note that, in the present context, it is customary to set the Boltzmann constant $k=1$). For example, by properties of the Borel functional calculus, we see that for any unitary operator U,

$S(\rho )\;=S(U\rho U^{*}).$

Indeed, without the above property, the von Neumann entropy would not be well-defined. In particular, U could be the time evolution operator of the system, i.e.

$U(t)\;=\exp \left({\frac {-iHt}{\hbar }}\right)$

where H is the Hamiltonian of the system. This associates the reversibility of a process with its resulting entropy change, i.e. a process is reversible if, and only if, it leaves the entropy of the system invariant. This provides a connection between quantum information theory and thermodynamics.

Applications of entanglement

Entanglement has many applications in quantum information theory. Mixed state entanglement can be viewed as a resource for quantum communication. With the aid of entanglement, otherwise impossible tasks may be achieved. Among the best known applications of entanglement are superdense coding and quantum state teleportation. Efforts to quantify this resource are often termed entanglement theory. Quantum entanglement also has many different applications in the emerging technologies of quantum computing and quantum cryptography, and has been used to realize quantum teleportation experimentally. At the same time, it prompts some of the more philosophically oriented discussions concerning quantum theory.{{carece de fontes}} The correlations predicted by quantum mechanics, and observed in experiment, reject the principle of local realism, which is that information about the state of a system can only be mediated by interactions in its immediate surroundings and that the state of a system exists and is well-defined before any measurement. Different views of what is actually occurring in the process of quantum entanglement can be related to different interpretations of quantum mechanics. In the previously standard one, the Copenhagen interpretation, quantum mechanics is neither "real" (since measurements do not state, but instead prepare properties of the system) nor "local" (since the state vector $|\psi \rangle$ comprises the simultaneous probability amplitudes for all positions, e.g. $|\psi \rangle \to \psi (x,y,z)$); the properties of entanglement are some of the many reasons why the Copenhagen Interpretation is no longer considered standard by a large proportion of the scientific community.

Other uses:

• Quantum computers use entanglement and superposition.
• The Reeh-Schlieder theorem of quantum field theory is sometimes seen as the QFT analogue of quantum entanglement.

See also

• Entanglement witness
• Separable states
• Squashed entanglement
• Quantum coherence
• Action at a distance (physics)
• Ghirardi-Rimini-Weber theory
• Quantum pseudo-telepathy
• Entanglement distillation
• Quantum mysticism

References

Predefinição:More footnotes Specific references:

General references:

External links

• Quantum Entanglement at Stanford Encyclopedia of Philosophy
• Entanglement experiment with photon pairs - interactive
• Multiple entanglement and quantum repeating
• How to entangle photons experimentally
• Quantum Entanglement
• Quantum Entanglement and Bell's Theorem at MathPages
• Recorded research seminars at Imperial College relating to quantum entanglement
• How Quantum Entanglement Works
• Quantum Entanglement and Decoherence: 3rd International Conference on Quantum Information (ICQI)
• The original EPR paper
• Ion trapping quantum information processing
• IEEE Spectrum On-line: The trap technique
• Was Einstein Wrong?: A Quantum Threat to Special Relativity

Category:Quantum information science Category:Quantum mechanics pt:Entrelaçamento quântico

Predefinição:Quantum mechanics An interpretation of quantum mechanics is a statement which attempts to explain how quantum mechanics informs our understanding of nature. Although quantum mechanics has received thorough experimental testing, many of these experiments are open to different interpretations. There exist a number of contending schools of thought, differing over whether quantum mechanics can be understood to be deterministic, which elements of quantum mechanics can be considered "real", and other matters.

Although today this question is of special interest to philosophers of physics, many physicists continue to show a strong interest in the subject. Physicists usually consider an interpretation of quantum mechanics as an interpretation of the mathematical formalism of quantum mechanics, specifying the physical meaning of the mathematical entities of the theory.

Historical background

The definition of terms used by researchers in quantum theory (such as wavefunctions and matrix mechanics) progressed through many stages. For instance, Schrödinger originally viewed the wavefunction associated with the electron as corresponding to the charge density of an object smeared out over an extended, possibly infinite, volume of space. Max Born interpreted it as simply corresponding to a probability distribution. These are two different interpretations of the wavefunction. In one it corresponds to a material field, in the other it "just" corresponds to a probability density.

Most physicists think quantum mechanics does not need interpretation.{{carece de fontes}} More precisely, they think it only requires an instrumentalist interpretation. Besides the instrumentalist interpretation, the Copenhagen interpretation is the most popular among physicists, followed by the many worlds and consistent histories interpretations.{{carece de fontes}} But it is also true that most physicists consider non-instrumental questions (in particular ontological questions) to be irrelevant to physics.{{carece de fontes}} They fall back on David Mermin's expression: "shut up and calculate" often attributed (perhaps erroneously) to Richard Feynman (see [11]).

Obstructions to direct interpretation

The difficulties of interpretation reflect a number of points about the orthodox description of quantum mechanics, including:

1. The abstract, mathematical nature of the description of quantum mechanics.
2. The existence of what appear to be non-deterministic and irreversible processes in quantum mechanics.
3. The phenomenon of entanglement, and in particular, the correlations between remote events that are not expected in classical theory.
4. The complementarity of possible descriptions of reality.
5. The essential role played by observers and the process of measurement in the theory.

First, the accepted mathematical structure of quantum mechanics is based on fairly abstract mathematics, such as Hilbert spaces and operators on those Hilbert spaces. In classical mechanics and electromagnetism, on the other hand, properties of a point mass or properties of a field are described by real numbers or functions defined on two or three dimensional sets. These have direct, spatial meaning, and in these theories there seems to be less need to provide a special interpretation for those numbers or functions.

Further, the process of measurement plays an essential role in the theory. Put simply: the world around us seems to be in a specific state, yet quantum mechanics describes it with wave functions governing the probabilities of values. In general the wave-function assigns non-zero probabilities to all possible values for a given physical quantity, such as position. How then is it that we come to see a particle at a specific position when its wave function is spread across all space? In order to describe how specific outcomes arise from the probabilities, the direct interpretation introduces the concept of measurement. According to the theory, wave functions interact with each other and evolve in time according to the laws of quantum mechanics until a measurement is performed, at which time the system will take on one of the possible values with probability governed by the wave-function. Measurement can interact with the system state in somewhat peculiar ways, as is illustrated by the double-slit experiment.

Thus the mathematical formalism used to describe the time evolution of a non-relativistic system proposes two somewhat different kinds of transformations:

• Reversible transformations described by unitary operators on the state space. These transformations are determined by solutions to the Schrödinger equation.

• Non-reversible and unpredictable transformations described by mathematically more complicated transformations (see quantum operations). Examples of these transformations are those that are undergone by a system as a result of measurement.

A restricted version of the problem of interpretation in quantum mechanics consists in providing some sort of plausible picture, just for the second kind of transformation. This problem may be addressed by purely mathematical reductions, for example by the many-worlds or the consistent histories interpretations.

In addition to the unpredictable and irreversible character of measurement processes, there are other elements of quantum physics that distinguish it sharply from classical physics and which cannot be represented by any classical picture. One of these is the phenomenon of entanglement, as illustrated in the EPR paradox, which seemingly violates principles of local causality .

Another obstruction to direct interpretation is the phenomenon of complementarity, which seems to violate basic principles of propositional logic. Complementarity says there is no logical picture (obeying classical propositional logic) that can simultaneously describe and be used to reason about all properties of a quantum system S. This is often phrased by saying that there are "complementary" sets A and B of propositions that can describe S, but not at the same time. Examples of A and B are propositions involving a wave description of S and a corpuscular description of S. The latter statement is one part of Niels Bohr's original formulation, which is often equated to the principle of complementarity itself.

Complementarity is not usually taken to mean that classical logic fails, although Hilary Putnam did take that view in his paper Is logic empirical?. Instead complementarity means that composition of physical properties for S (such as position and momentum both having values in certain ranges) using propositional connectives does not obey rules of classical propositional logic. As is now well-known (Omnès, 1999) the "origin of complementarity lies in the noncommutativity of operators" describing observables in quantum mechanics.

Problematic status of pictures and interpretations

The precise ontological status, of each one of the interpreting pictures, remains a matter of philosophical argument.

In other words, if we interpret the formal structure X of quantum mechanics by means of a structure Y (via a mathematical equivalence of the two structures), what is the status of Y? This is the old question of saving the phenomena, in a new guise.

Some physicists, for example Asher Peres and Chris Fuchs, seem to argue that an interpretation is nothing more than a formal equivalence between sets of rules for operating on experimental data. This would suggest that the whole exercise of interpretation is unnecessary.

Instrumentalist interpretation

Any modern scientific theory requires at the very least an instrumentalist description which relates the mathematical formalism to experimental practice and prediction. In the case of quantum mechanics, the most common instrumentalist description is an assertion of statistical regularity between state preparation processes and measurement processes. That is, if a measurement of a real-valued quantity is performed many times, each time starting with the same initial conditions, the outcome is a well-defined probability distribution over the real numbers; moreover, quantum mechanics provides a computational instrument to determine statistical properties of this distribution, such as its expectation value.

Calculations for measurements performed on a system S postulate a Hilbert space H over the complex numbers. When the system S is prepared in a pure state, it is associated with a vector in H. Measurable quantities are associated with Hermitian operators acting on H: these are referred to as observables.

Repeated measurement of an observable A for S prepared in state ψ yields a distribution of values. The expectation value of this distribution is given by the expression

$\langle \psi \vert A\vert \psi \rangle .$

This mathematical machinery gives a simple, direct way to compute a statistical property of the outcome of an experiment, once it is understood how to associate the initial state with a Hilbert space vector, and the measured quantity with an observable (that is, a specific Hermitian operator).

As an example of such a computation, the probability of finding the system in a given state $\vert \phi \rangle$ is given by computing the expectation value of a (rank-1) projection operator

$\Pi =\vert \phi \rangle \langle \phi \vert$

The probability is then the non-negative real number given by

$P=\langle \psi \vert \Pi \vert \psi \rangle =\vert \langle \psi \vert \phi \rangle \vert ^{2}.$

By abuse of language, the bare instrumentalist description can be referred to as an interpretation, although this usage is somewhat misleading since instrumentalism explicitly avoids any explanatory role; that is, it does not attempt to answer the question of what quantum mechanics is talking about.

Summary of common interpretations of QM

Properties of interpretations

An interpretation can be characterized by whether it satisfies certain properties, such as:

• Realism
• Completeness
• Local realism
• Determinism

To explain these properties, we need to be more explicit about the kind of picture an interpretation provides. To that end we will regard an interpretation as a correspondence between the elements of the mathematical formalism M and the elements of an interpreting structure I, where:

• The mathematical formalism consists of the Hilbert space machinery of ket-vectors, self-adjoint operators acting on the space of ket-vectors, unitary time dependence of ket-vectors and measurement operations. In this context a measurement operation can be regarded as a transformation which carries a ket-vector into a probability distribution on ket-vectors. See also quantum operations for a formalization of this concept.
• The interpreting structure includes states, transitions between states, measurement operations and possibly information about spatial extension of these elements. A measurement operation here refers to an operation which returns a value and results in a possible system state change. Spatial information, for instance would be exhibited by states represented as functions on configuration space. The transitions may be non-deterministic or probabilistic or there may be infinitely many states. However, the critical assumption of an interpretation is that the elements of I are regarded as physically real.

In this sense, an interpretation can be regarded as a semantics for the mathematical formalism.

In particular, the bare instrumentalist view of quantum mechanics outlined in the previous section is not an interpretation at all since it makes no claims about elements of physical reality.

The current use in physics of "completeness" and "realism" is often considered to have originated in the paper (Einstein et al., 1935) which proposed the EPR paradox. In that paper the authors proposed the concept "element of reality" and "completeness" of a physical theory. Though they did not define "element of reality", they did provide a sufficient characterization for it, namely a quantity whose value can be predicted with certainty before measuring it or disturbing it in any way. EPR define a "complete physical theory" as one in which every element of physical reality is accounted for by the theory. In the semantic view of interpretation, an interpretation of a theory is complete if every element of the interpreting structure is accounted for by the mathematical formalism. Realism is a property of each one of the elements of the mathematical formalism; any such element is real if it corresponds to something in the interpreting structure. For instance, in some interpretations of quantum mechanics (such as the many-worlds interpretation) the ket vector associated to the system state is assumed to correspond to an element of physical reality, while in others it does not.

Determinism is a property characterizing state changes due to the passage of time, namely that the state at an instant of time in the future is a function of the state at the present (see time evolution). It may not always be clear whether a particular interpreting structure is deterministic or not, precisely because there may not be a clear choice for a time parameter. Moreover, a given theory may have two interpretations, one of which is deterministic, and the other not.

Local realism has two parts:

• The value returned by a measurement corresponds to the value of some function on the state space. Stated in another way, this value is an element of reality;
• The effects of measurement have a propagation speed not exceeding some universal bound (e.g., the speed of light). In order for this to make sense, measurement operations must be spatially localized in the interpreting structure.

A precise formulation of local realism in terms of a local hidden variable theory was proposed by John Bell.

Bell's theorem, combined with experimental testing, restricts the kinds of properties a quantum theory can have. For instance, the experimental rejection of Bell's theorem implies that quantum mechanics cannot satisfy local realism.

Ensemble interpretation, or statistical interpretation

The Ensemble interpretation, or statistical interpretation, can be viewed as a minimalist interpretation. That is, it claims to make the fewest assumptions associated with the standard mathematical formalization. At its heart, it takes the statistical interpretation of Born to the fullest extent. The interpretation states that the wave function does not apply to an individual system, or for example, a single particle, but is an abstract mathematical, statistical quantity that only applies to an ensemble of similar prepared systems or particles. Probably the most notable supporter of such an interpretation was Einstein:

The attempt to conceive the quantum-theoretical description as the complete description of the individual systems leads to unnatural theoretical interpretations, which become immediately unnecessary if one accepts the interpretation that the description refers to ensembles of systems and not to individual systems.

— Einstein in Albert Einstein: Philosopher-Scientist, ed. P.A. Schilpp (Harper & Row, New York)

Probably the most prominent current advocate of the ensemble interpretation is Leslie E. Ballentine, Professor at Simon Fraser University, and writer of the graduate level text book Quantum Mechanics, A Modern Development.

Experimental evidence favouring the ensemble interpretation is provided in a particularly clear way in Akira Tonomura's Video clip 1[12], presenting results of a double-slit experiment with an ensemble of individual electrons. It is evident from this experiment that, since the quantum mechanical wave function describes the final interference pattern, it must describe the ensemble rather than an individual electron, the latter being seen to yield a pointlike impact on a screen.

The Copenhagen interpretation

The Copenhagen interpretation is the "standard" interpretation of quantum mechanics formulated by Niels Bohr and Werner Heisenberg while collaborating in Copenhagen around 1927. Bohr and Heisenberg extended the probabilistic interpretation of the wavefunction, proposed by Max Born. The Copenhagen interpretation rejects questions like "where was the particle before I measured its position" as meaningless. The measurement process randomly picks out exactly one of the many possibilities allowed for by the state's wave function.

Participatory Anthropic Principle (PAP)

Predefinição:Main article Viewed by some as mysticism (see "consciousness causes collapse"), Wheeler's Participatory Anthropic Principle is the speculative theory that observation by a conscious observer is responsible for the wavefunction collapse. It is an attempt to solve Wigner's friend paradox by simply stating that collapse occurs at the first "conscious" observer. Supporters claim PAP is not a revival of substance dualism, since (in one ramification of the theory) consciousness and objects are entangled and cannot be considered as distinct. Although such an idea could be added to other interpretations of quantum mechanics, PAP was added to the Copenhagen interpretation (Wheeler studied in Copenhagen under Niels Bohr in the 1930s). It is possible an experiment could be devised to test this theory, since it depends on an observer to collapse a wavefunction. The observer has to be conscious, but whether Schrödinger's cat or a person is necessary would be part of the experiment (hence a successful experiment could also define consciousness). However, the experiment would need to be carefully designed as, in Wheeler's view, it would need to ensure for an unobserved event that it remained unobserved for all time .

Consistent histories

The consistent histories generalizes the conventional Copenhagen interpretation and attempts to provide a natural interpretation of quantum cosmology. The theory is based on a consistency criterion that allows the history of a system to be described so that the probabilities for each history obey the additive rules of classical probability. It is claimed to be consistent with the Schrödinger equation.

According to this interpretation, the purpose of a quantum-mechanical theory is to predict the relative probabilities of various alternative histories.

Objective collapse theories

Ver artigo principal: Objective collapse theory

Objective collapse theories differ from the Copenhagen interpretation in regarding both the wavefunction and the process of collapse as ontologically objective. In objective theories, collapse occurs randomly ("spontaneous localization"), or when some physical threshold is reached, with observers having no special role. Thus, they are realistic, indeterministic, no-hidden-variables theories. The mechanism of collapse is not specified by standard quantum mechanics, which needs to be extended if this approach is correct, meaning that Objective Collapse is more of a theory than an interpretation. Examples include the Ghirardi-Rimini-Weber theory and the Penrose interpretation.

Many worlds

The many-worlds interpretation (or MWI) is an interpretation of quantum mechanics that rejects the non-deterministic and irreversible wavefunction collapse associated with measurement in the Copenhagen interpretation in favor of a description in terms of quantum entanglement and reversible time evolution of states. The phenomena associated with measurement are claimed to be explained by decoherence which occurs when states interact with the environment. As result of the decoherence the world-lines of macroscopic objects repeatedly split into mutually unobservable, branching histories—distinct universes within a greater multiverse.

Stochastic mechanics

An entirely classical derivation and interpretation of the Schrödinger equation by analogy with Brownian motion was suggested by Princeton University professor Edward Nelson in 1966 (“Derivation of the Schrödinger Equation from Newtonian Mechanics”, Phys. Rev. 150, 1079-1085). Similar considerations were published already before, e.g. by R. Fürth (1933), I. Fényes (1952), Walter Weizel (1953), and are referenced in Nelson's paper. More recent work on the subject can be found in M. Pavon, “Stochastic mechanics and the Feynman integral”, J. Math. Phys. 41, 6060-6078 (2000). An alternative stochastic interpretation was suggested by Roumen Tsekov.

The decoherence approach

Predefinição:Main article Decoherence occurs when a system interacts with its environment, or any complex external system, in such a thermodynamically irreversible way that ensures different elements in the quantum superposition of the system+environment's wave function can no longer (or are extremely unlikely to) interfere with each other. Decoherence does not provide a mechanism for the actual wave function collapse; rather, it is claimed that it provides a mechanism for the appearance of wave function collapse. The quantum nature of the system is simply "leaked" into the environment so that a total superposition of the wave function still exists, but cannot be detected by experiments that (so far) can be carried out in practice.

Many minds

The many-minds interpretation of quantum mechanics extends the many-worlds interpretation by proposing that the distinction between worlds should be made at the level of the mind of an individual observer.

Quantum logic

Quantum logic can be regarded as a kind of propositional logic suitable for understanding the apparent anomalies regarding quantum measurement, most notably those concerning composition of measurement operations of complementary variables. This research area and its name originated in the 1936 paper by Garrett Birkhoff and John von Neumann, who attempted to reconcile some of the apparent inconsistencies of classical boolean logic with the facts related to measurement and observation in quantum mechanics.

The Bohm interpretation

The Bohm interpretation of quantum mechanics is a theory by David Bohm in which particles, which always have positions, are guided by the wavefunction. The wavefunction evolves according to the Schrödinger wave equation, which never collapses. The theory takes place in a single space-time, is non-local, and is deterministic. The simultaneous determination of a particle's position and velocity is subject to the usual uncertainty principle constraints, which is why the theory was originally called one of "hidden" variables.

It has been shown to be empirically equivalent to the Copenhagen interpretation. The measurement problem is claimed to be resolved by the particles having definite positions at all times . Collapse is explained as phenomenological.

Transactional interpretation

The transactional interpretation of quantum mechanics (TIQM) by John G. Cramer [13] is an interpretation of quantum mechanics inspired by the contribution Richard Feynman made to Quantum Electrodynamics. It describes quantum interactions in terms of a standing wave formed by retarded (forward-in-time) and advanced (backward-in-time) waves. The author argues that it avoids the philosophical problems with the Copenhagen interpretation and the role of the observer, and resolves various quantum paradoxes.

Relational quantum mechanics

The essential idea behind relational quantum mechanics, following the precedent of special relativity, is that different observers may give different accounts of the same series of events: for example, to one observer at a given point in time, a system may be in a single, "collapsed" eigenstate, while to another observer at the same time, it may be in a superposition of two or more states. Consequently, if quantum mechanics is to be a complete theory, relational quantum mechanics argues that the notion of "state" describes not the observed system itself, but the relationship, or correlation, between the system and its observer(s). The state vector of conventional quantum mechanics becomes a description of the correlation of some degrees of freedom in the observer, with respect to the observed system. However, it is held by relational quantum mechanics that this applies to all physical objects, whether or not they are conscious or macroscopic. Any "measurement event" is seen simply as an ordinary physical interaction, an establishment of the sort of correlation discussed above. Thus the physical content of the theory is to do not with objects themselves, but the relations between them [14]. For more information, see Rovelli (1996).

An independent relational approach to quantum mechanics was developed in analogy with David Bohm's elucidation of special relativity (The Special Theory of Relativity, Benjamin, New York, 1965), in which a detection event is regarded as establishing a relationship between the quantized field and the detector. The inherent ambiguity associated with applying Heisenberg's uncertainty principle is subsequently avoided [15]. For a full account [16], see Zheng et al. (1992, 1996).

Modal interpretations of quantum theory

Modal interpretations of quantum mechanics were first conceived of in 1972 by B. van Fraassen, in his paper “A formal approach to the philosophy of science.” However, this term now is used to describe a larger set of models that grew out of this approach. The Stanford Encyclopedia of Philosophy describes several versions:

• The Copenhagen variant
• Kochen-Dieks-Healey Interpretations
• Motivating Early Modal Interpretations, based on the work of R. Clifton, M. Dickson and J. Bub.

Incomplete measurements

The theory of incomplete measurements (TIM) derives the main axioms of quantum mechanics from properties of the physical processes that are acceptable measurements. In that interpretation:

• wavefunctions collapse because we require measurements to give consistent and repeatable results.
• wavefunctions are complex-valued because they represent a field of "found/not-found" probabilities.
• eigenvalue equations are associated with symbolic values of measurements, which we often choose to be real numbers.

The TIM is more than a simple interpretation of quantum mechanics, since in that theory, both general relativity and the traditional formalism of quantum mechanics are seen as approximations. However, it does give an interesting interpretation to quantum mechanics.

Comparison

The most common interpretations are summarized in the table below. The values shown in the cells of the table are not without controversy, for the precise meanings of some of the concepts involved are unclear and, in fact, are themselves at the center of the controversy surrounding the given interpretation.

No experimental evidence exists that distinguishes among these interpretations. To that extent, the physical theory stands, and is consistent with itself and with reality; difficulties arise only when one attempts to "interpret" the theory. Nevertheless, designing experiments which would test the various interpretations is the subject of active research.

Most of these interpretations have variants. For example, it is difficult to get a precise definition of the Copenhagen interpretation. The table below gives two variants: one that regards the waveform as being a tool for calculating probabilities only, and the other regards the waveform as an "element of reality."

Interpretation	Deterministic?	Wavefunction real?	Unique history?	Hidden variables?	Collapsing wavefunctions?	Observer role?
Stochastic mechanics	No	No	Yes	No	No	None
Ensemble interpretation (Waveform not real)	No	No	Yes	Agnostic	No	None
Copenhagen interpretation (Waveform not real)	No	No	Yes	No	NA	NA
Copenhagen interpretation (Waveform real) Objective collapse theories	No	Yes	Yes	No	Yes	None
Copenhagen interpretation (Waveform real) PAP	No	Yes	Yes	No	Yes	Causal
Many-worlds interpretation (Decoherent approach)	Yes	Yes	No	No	No	None
Many-minds interpretation	Yes	Yes	No	No	No	Interpretational4
Consistent histories (Decoherent approach)	Agnostic1	Agnostic1	No	No	No	Interpretational²
Quantum logic	Agnostic	Agnostic	Yes³	No	No	Interpretational²
Bohm-de Broglie interpretation ("Pilot-wave" approach)	Yes	Yes5	Yes6	Yes	No	None
Transactional interpretation	No	Yes	Yes	No	Yes7	None
Relational Quantum Mechanics	No	Yes	Agnostic8	No	Yes9	None
Incomplete measurements	No	No10	Yes	No	Yes10	Interpretational²

¹ If wavefunction is real then this becomes the many-worlds interpretation. If wavefunction less than real, but more than just information, then Zurek calls this the "existential interpretation".
² Quantum mechanics is regarded as a way of predicting observations, or a theory of measurement..
³ But quantum logic is more limited in applicability than Coherent Histories.
⁴ Observers separate the universal wavefunction into orthogonal sets of experiences.
⁵ Both particle AND guiding wavefunction are real.
⁶ Unique particle history, but multiple wave histories.
⁷ In the TI the collapse of the state vector is interpreted as the completion of the transaction between emitter and absorber.
⁸ Comparing histories between systems in this interpretation has no well-defined meaning.
⁹ Any physical interaction is treated as a collapse event relative to the systems involved, not just macroscopic or conscious observers.
¹⁰ The nature and collapse of the wavefunction are derived, not axiomatic.

See also

• Afshar experiment
• Bell's theorem
• Bohm interpretation
• Bohr-Einstein debates
• Consistent Histories
• Copenhagen interpretation
• Ghirardi-Rimini-Weber theory
• Many-minds interpretation
• Many-worlds interpretation
• Measurement problem
• Minority interpretations of quantum mechanics
• Objective collapse theory
• Penrose Interpretation
• Philosophical interpretation of classical physics

• Pondicherry interpretation
• Quantum computation
• Quantum decoherence
• Quantum entanglement
• Quantum gravity
• Quantum indeterminacy
• Quantum mechanics
• Quantum mysticism
• Quantum Zeno effect
• Relational quantum mechanics
• Theory of incomplete measurements
• Transactional interpretation
• Wave function collapse

References

• Bub, J. and Clifton, R. 1996. “A uniqueness theorem for interpretations of quantum mechanics,” Studies in History and Philosophy of Modern Physics, 27B, 181-219
• R. Carnap, The interpretation of physics, Foundations of Logic and Mathematics of the International Encyclopedia of Unified Science, University of Chicago Press, 1939.
• D. Deutsch, The Fabric of Reality, Allen Lane, 1997. Though written for general audiences, in this book Deutsch argues forcefully against instrumentalism.
• Dickson, M. 1994. Wavefunction tails in the modal interpretation, Proceedings of the PSA 1994, Hull, D., Forbes, M., and Burian, R. (eds), Vol. 1, pp. 366–376. East Lansing, Michigan: Philosophy of Science Association.
• Dickson, M. and Clifton, R. 1998. Lorentz-invariance in modal interpretations The Modal Interpretation of Quantum Mechanics, Dieks, D. and Vermaas, P. (eds), pp. 9–48. Dordrecht: Kluwer Academic Publishers
• A. Einstein, B. Podolsky and N. Rosen, Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47 777, 1935.
• C. Fuchs and A. Peres, Quantum theory needs no ‘interpretation’ , Physics Today, March 2000.
• Christopher Fuchs, Quantum Mechanics as Quantum Information (and only a little more), arXiv:quant-ph/0205039 v1, (2002)
• N. Herbert. Quantum Reality: Beyond the New Physics, New York: Doubleday, ISBN 0-385-23569-0, LoC QC174.12.H47 1985.
• T. Hey and P. Walters, The New Quantum Universe, New York: Cambridge University Press, 2003, ISBN 0-5215-6457-3.
• R. Jackiw and D. Kleppner, One Hundred Years of Quantum Physics, Science, Vol. 289 Issue 5481, p893, August 2000.
• M. Jammer, The Conceptual Development of Quantum Mechanics. New York: McGraw-Hill, 1966.
• M. Jammer, The Philosophy of Quantum Mechanics. New York: Wiley, 1974.
• Al-Khalili, Quantum: A Guide for the Perplexed. London: Weidenfeld & Nicholson, 2003.
• W. M. de Muynck, Foundations of quantum mechanics, an empiricist approach, Dordrecht: Kluwer Academic Publishers, 2002, ISBN 1-4020-0932-1
• R. Omnès, Understanding Quantum Mechanics, Princeton, 1999.
• K. Popper, Conjectures and Refutations, Routledge and Kegan Paul, 1963. The chapter "Three views Concerning Human Knowledge", addresses, among other things, the instrumentalist view in the physical sciences.
• H. Reichenbach, Philosophic Foundations of Quantum Mechanics, Berkeley: University of California Press, 1944.
• C. Rovelli, Relational Quantum Mechanics; Int. J. of Theor. Phys. 35 (1996) 1637. arXiv: quant-ph/9609002 [17]
• Q. Zheng and T. Kobayashi, Quantum Optics as a Relativistic Theory of Light; Physics Essays 9 (1996) 447. Annual Report, Department of Physics, School of Science, University of Tokyo (1992) 240.
• M. Tegmark and J. A. Wheeler, 100 Years of Quantum Mysteries", Scientific American 284, 68, 2001.
• van Fraassen, B. 1972. A formal approach to the philosophy of science, in Paradigms and Paradoxes: The Philosophical Challenge of the Quantum Domain, Colodny, R. (ed.), pp. 303–366. Pittsburgh: University of Pittsburgh Press.
• John A. Wheeler and Wojciech Hubert Zurek (eds), Quantum Theory and Measurement, Princeton: Princeton University Press, ISBN 0-691-08316-9, LoC QC174.125.Q38 1983.

Further reading

• David Z Albert, Quantum Mechanics and Experience, ISBN 0674741129
• J S Bell, Speakable and unspeakable in Quantum Mechanics, ISBN 0521523389
• David Bohm, Wholeness and the Implicate Order, ISBN 0-7100-0971-2
• David Deutsch, The Fabric of Reality, ISBN 014027541X
• Bernard d'Espagnat, Reality and the physicist, ISBN 0521338468
• Bernard d'Espagnat, In search of Reality, ISBN 0387113991
• Bernard d'Espagnat, Conceptual Foundation of Quantum Mechanics, ISBN 081334087X
• Arthur Fine, The Shaky Game: Einstein Realism and the Quantum Theory. Science and its Conceptual Foundations. Chicago, 1986], ISBN 0226249484
• Roland Omnes, The Interpretation of Quantum Mechanics, ISBN 0691036691
• Roger Penrose, The Emperor's New Mind, ISBN 0-198-51973-7
• Roger Penrose, Shadows of the Mind, ISBN 0-19-853978-9

External links

• Willem M. de Muynck Broad overview, realist vs. empiricist interpretations, against oversimplified view of the measurement process
• Skeptical View of "New Age" Interpretations of QM
• The many worlds of quantum mechanics
• Erich Joos' Decoherence Website Basic and in-depth information on decoherence
• Quantum Mechanics for Philosophers An argument for the superiority of the Bohm interpretation.
• Many-Worlds Interpretation of Quantum Mechanics
• Numerous Many Worlds-related Topics and Articles
• Relational Quantum Mechanics
• Relational Approach to Quantum Physics
• Theory of incomplete measurements Deriving quantum mechanics axioms from properties of acceptable measurements.
• Schreiber, Z. - The Nine Lives of Schrodinger's Cat (overview of interpretations)
• Alfred Neumaier's FAQ
• Measurement in Quantum Mechanics FAQ
• Interpretation of quantum mechanics on arxiv.org

Category:Quantum mechanics pt:Interpretações da mecânica quântica

Predefinição:Quantum mechanics The Copenhagen interpretation is an interpretation of quantum mechanics. A key feature of quantum mechanics is that the state of every particle is described by a wavefunction, which is a mathematical representation used to calculate the probability for it to be found in a location or a state of motion. In effect, the act of measurement causes the calculated set of probabilities to "collapse" to the value defined by the measurement. This feature of the mathematical representations is known as wavefunction collapse.

Early twentieth-century experiments on the physics of very small-scale phenomena led to the discovery of phenomena that could not be predicted on the basis of classical physics, and to new empirical generalizations (theories) that described and predicted very accurately those micro-scale phenomena so recently discovered. These generalizations, these models of the real world being observed at this micro scale, could not be squared easily with the way objects are observed to behave on the macro scale of everyday life. The predictions they offered often appeared counter-intuitive to observers. Indeed, they touched off much consternation -- even in the minds of their discoverers. The Copenhagen interpretation consists of attempts to explain the experiments and their mathematical formulations in ways that do not go beyond the evidence to suggest more (or less) than is actually there.

The work of relating the experiments and the abstract mathematical and theoretical formulations that constitute quantum physics to the experience that all of us share in the world of everyday life fell first to Niels Bohr and Werner Heisenberg in the course of their collaboration in Copenhagen around 1927. Bohr and Heisenberg stepped beyond the world of empirical experiments and pragmatic predictions of such phenomena as the frequencies of light emitted under various conditions. In the earlier work of Planck, Einstein and Bohr himself, discrete quantities of energy had been postulated in order to avoid paradoxes of classical physics when pushed to extremes. Bohr and Heisenberg now found a new world of energy quanta, entities that fit neither the classical ideas of particles nor the classical ideas of waves. Elementary particles behaved in ways highly regular when many similar interactions were analyzed yet, highly unpredictable when one tried to predict things like individual trajectories through a simple physical apparatus.

The new theories were inspired by laboratory experiments and based on the idea that matter has both wave and particle aspects. One of the consequences, derived by Heisenberg, was that knowledge of the position of a particle limits how precisely its momentum can be known – and vice-versa. The results of their own burgeoning understanding disoriented Bohr and Heisenberg, and some physicists concluded that human observation of a microscopic event changes the reality of the event.

The Copenhagen interpretation was a composite statement about what could and could not be legitimately stated in common language to complement the statements and predictions that could be made in the language of instrument readings and mathematical operations. In other words, it attempted to answer the question, "What do these amazing experimental results really mean?"

Overview

There is no definitive statement of the Copenhagen Interpretation since it consists of the views developed by a number of scientists and philosophers at the turn of the 20th century. Thus, there are a number of ideas that have been associated with the Copenhagen interpretation. Asher Peres remarked that very different, sometimes opposite, views are presented as "the Copenhagen interpretation" by different authors.

Principles

1. A system is completely described by a wave function $\psi$, which represents an observer's knowledge of the system. (Heisenberg)  
2. The description of nature is essentially probabilistic. The probability of an event is related to the square of the amplitude of the wave function related to it. (Born rule, due to Max Born)
3. Heisenberg's uncertainty principle states the observed fact that it is not possible to know the values of all of the properties of the system at the same time; those properties that are not known with precision must be described by probabilities.
4. Complementarity principle: matter exhibits a wave-particle duality. An experiment can show the particle-like properties of matter, or wave-like properties, but not both at the same time.(Niels Bohr)
5. Measuring devices are essentially classical devices, and measure classical properties such as position and momentum.
6. The correspondence principle of Bohr and Heisenberg: the quantum mechanical description of large systems should closely approximate the classical description.

The meaning of the wave function

The Copenhagen Interpretation denies that any wave function is anything more than an abstraction, or is at least non-committal about its being a discrete entity or a discernible component of some discrete entity.

There are some who say that there are objective variants of the Copenhagen Interpretation that allow for a "real" wave function, but it is questionable whether that view is really consistent with positivism and/or with some of Bohr's statements. Niels Bohr emphasized that science is concerned with predictions of the outcomes of experiments, and that any additional propositions offered are not scientific but rather meta-physical. Bohr was heavily influenced by positivism. On the other hand, Bohr and Heisenberg were not in complete agreement, and held different views at different times. Heisenberg in particular was prompted to move towards realism.

Even if the wave function is not regarded as real, there is still a divide between those who treat it as definitely and entirely subjective, and those who are non-committal or agnostic about the subject.

An example of the agnostic view is given by von Weizsäcker, who, while participating in a colloquium at Cambridge, denied that the Copenhagen interpretation asserted: "What cannot be observed does not exist". He suggested instead that the Copenhagen interpretation follows the principle: "What is observed certainly exists; about what is not observed we are still free to make suitable assumptions. We use that freedom to avoid paradoxes."

The subjective view, that the wave function is merely a mathematical tool for calculating probabilities of specific experiment, is a similar approach to the Ensemble interpretation.

The nature of collapse

All versions of the Copenhagen interpretation include at least a formal or methodological version of wave function collapse, in which unobserved eigenvalues are removed from further consideration. (In other words, Copenhagenists have never rejected collapse, even in the early days of quantum physics, in the way that adherents of the Many-worlds interpretation do.) In more prosaic terms, those who hold to the Copenhagen understanding are willing to say that a wave function involves the various probabilities that a given event will proceed to certain different outcomes. But when one or another of those more- or less-likely outcomes becomes manifest the other probabilities cease to have any function in the real world. So if an electron passes through a double slit apparatus there are various probabilities for where on the detection screen that individual electron will hit. But once it has hit, there is no longer any probability whatsoever that it will hit somewhere else. Many-worlds interpretations say that an electron hits wherever there is a possibility that it might hit, and that each of these hits occurs in a separate universe.

An adherent of the subjective view, that the wave function represents nothing but knowledge, would take an equally subjective view of "collapse".

Some argue that the concept of collapse of a "real" wave function was introduced by John Von Neumann in 1932 and was not part of the original formulation of the Copenhagen Interpretation.

Acceptance among physicists

According to a poll at a Quantum Mechanics workshop in 1997, the Copenhagen interpretation is the most widely-accepted specific interpretation of quantum mechanics, followed by the many-worlds interpretation. Although current trends show substantial competition from alternative interpretations, throughout much of the twentieth century the Copenhagen interpretation had strong acceptance among physicists. Astrophysicist and science writer John Gribbin describes it as having fallen from primacy after the 1980s.

Consequences

The nature of the Copenhagen Interpretation is exposed by considering a number of experiments and paradoxes.

1. Schrödinger's Cat - A cat is put in a box with a radioactive substance and a radiation detector (such as a geiger counter). The half-life of the substance is the period of time in which there is a 50% chance that a particle will be emitted (and detected). The detector is activated for that period of time. If a particle is detected, a poisonous gas will be released and the cat killed. Schrödinger set this up as what he called a "ridiculous case" in which "The psi-function of the entire system would express this by having in it the living and dead cat (pardon the expression) mixed or smeared out in equal parts." He resisted an interpretation "so naively accepting as valid a 'blurred model' for representing reality." How can the cat be both alive and dead?

The Copenhagen Interpretation: The wave function reflects our knowledge of the system. The wave function $(|{\text{dead}}\rangle +|{\text{alive}}\rangle )/{\sqrt {2}}$ simply means that there is a 50-50 chance that the cat is alive or dead.

2. Wigner's Friend - Wigner puts his friend in with the cat. The external observer believes the system is in the state $(|{\text{dead}}\rangle +|{\text{alive}}\rangle )/{\sqrt {2}}$. His friend however is convinced that cat is alive, i.e. for him, the cat is in the state $|{\text{alive}}\rangle$. How can Wigner and his friend see different wave functions?

The Copenhagen Interpretation: Wigner's friend highlights the subjective nature of probability. Each observer (Wigner and his friend) has different information and therefore different wave functions. The distinction between the "objective" nature of reality and the subjective nature of probability has led to a great deal of controversy. Cf. Bayesian versus Frequentist interpretations of probability.

3. Double Slit Diffraction - Light passes through double slits and onto a screen resulting in a diffraction pattern. Is light a particle or a wave?

The Copenhagen Interpretation: Light is neither. A particular experiment can demonstrate particle (photon) or wave properties, but not both at the same time (Bohr's Complementary Principle).

The same experiment can in theory be performed with any physical system: electrons, protons, atoms, molecules, viruses, bacteria, cats, humans, elephants, planets, etc. In practice it has been performed for light, electrons, buckminsterfullerene, and some atoms. Due to the smallness of Planck's constant it is practically impossible to realize experiments that directly reveal the wave nature of any system bigger than a few atoms but, in general, quantum mechanics considers all matter as possessing both particle and wave behaviors. The greater systems (like viruses, bacteria, cats, etc.) are considered as "classical" ones but only as an approximation.

4. EPR (Einstein–Podolsky–Rosen) paradox. Entangled "particles" are emitted in a single event. Conservation laws ensure that the measured spin of one particle must be the opposite of the measured spin of the other, so that if the spin of one particle is measured, the spin of the other particle is now instantaneously known. The most discomforting aspect of this paradox is that the effect is instantaneous so that something that happens in one galaxy could cause an instantaneous change in another galaxy. But, according to Einstein's theory of special relativity, no information-bearing signal or entity can travel at or faster than the speed of light, which is finite. Thus, it seems as if the Copenhagen interpretation is inconsistent with special relativity.

The Copenhagen Interpretation: Assuming wave functions are not real, wave function collapse is interpreted subjectively. The moment one observer measures the spin of one particle, he knows the spin of the other. However another observer cannot benefit until the results of that measurement have been relayed to him, at less than or equal to the speed of light.

Copenhagenists claim that interpretations of quantum mechanics where the wave function is regarded as real have problems with EPR-type effects, since they imply that the laws of physics allow for influences to propagate at speeds greater than the speed of light. However, proponents of Many worlds and the Transactional interpretation maintain that their theories are fatally non-local.

The claim that EPR effects violate the principle that information cannot travel faster than the speed of light can be avoided by noting that they cannot be used for signaling because neither observer can control, or predetermine, what he observes, and therefore cannot manipulate what the other observer measures. Relativistic difficulties about establishing which measurement occurred first also undermine the idea that one observer is causing what the other is measuring.{{carece de fontes}}

Criticisms

The completeness of quantum mechanics (thesis 1) was attacked by the Einstein-Podolsky-Rosen thought experiment which was intended to show that quantum physics could not be a complete theory.

Experimental tests of Bell's inequality using particles have supported the quantum mechanical prediction of entanglement.

The Copenhagen Interpretation gives special status to measurement processes without clearly defining them or explaining their peculiar effects. In his article entitled "Criticism and Counterproposals to the Copenhagen Interpretation of Quantum Theory," countering the view of Alexandrov that (in Heisenberg's paraphrase) "the wave function in configuration space characterizes the objective state of the electron." Heisenberg says,

Of course the introduction of the observer must not be misunderstood to imply that some kind of subjective features are to be brought into the description of nature. The observer has, rather, only the function of registering decisions, i.e., processes in space and time, and it does not matter whether the observer is an apparatus or a human being; but the registration, i.e., the transition from the "possible" to the "actual," is absolutely necessary here and cannot be omitted from the interpretation of quantum theory.

-- Heisenberg, Physics and Philosophy, p. 137

Many physicists and philosophers have objected to the Copenhagen interpretation, both on the grounds that it is non-deterministic and that it includes an undefined measurement process that converts probability functions into non-probabilistic measurements. Einstein's comments "I, at any rate, am convinced that He (God) does not throw dice." and "Do you really think the moon isn't there if you aren't looking at it?" exemplify this. Bohr, in response, said "Einstein, don't tell God what to do".

Steven Weinberg in "Einstein's Mistakes", Physics Today, November 2005, page 31, said:

All this familiar story is true, but it leaves out an irony. Bohr's version of quantum mechanics was deeply flawed, but not for the reason Einstein thought. The Copenhagen interpretation describes what happens when an observer makes a measurement, but the observer and the act of measurement are themselves treated classically. This is surely wrong: Physicists and their apparatus must be governed by the same quantum mechanical rules that govern everything else in the universe. But these rules are expressed in terms of a wave function (or, more precisely, a state vector) that evolves in a perfectly deterministic way. So where do the probabilistic rules of the Copenhagen interpretation come from?

Considerable progress has been made in recent years toward the resolution of the problem, which I cannot go into here. It is enough to say that neither Bohr nor Einstein had focused on the real problem with quantum mechanics. The Copenhagen rules clearly work, so they have to be accepted. But this leaves the task of explaining them by applying the deterministic equation for the evolution of the wave function, the Schrödinger equation, to observers and their apparatus.

The problem of thinking in terms of classical measurements of a quantum system becomes particularly acute in the field of quantum cosmology, where the quantum system is the universe.

Alternatives

Mais informações: [[:Interpretation of quantum mechanics]]

The Ensemble Interpretation is similar; it offers an interpretation of the wave function, but not for single particles. The consistent histories interpretation advertises itself as "Copenhagen done right". Consciousness causes collapse is often confused with the Copenhagen interpretation.

If the wave function is regarded as ontologically real, and collapse is entirely rejected, a many worlds theory results. If wave function collapse is regarded as ontologically real as well, an objective collapse theory is obtained. Dropping the principle that the wave function is a complete description results in a hidden variable theory.

Many physicists have subscribed to the null interpretation of quantum mechanics summarized by the sentence "Shut up and calculate!". While it is sometimes attributed to Paul Dirac or Richard Feynman, it is in fact due to David Mermin.

See also

• Afshar experiment
• Bohr-Einstein debates
• Consciousness causes collapse
• Consistent Histories
• Ensemble Interpretation
• Interpretation of quantum mechanics
• Philosophical interpretation of classical physics
• Popper's experiment

Further reading

• G. Weihs et al., Phys. Rev. Lett. 81 (1998) 5039
• M. Rowe et al., Nature 409 (2001) 791.
• J.A. Wheeler & W.H. Zurek (eds) , Quantum Theory and Measurement, Princeton University Press 1983
• A. Petersen, Quantum Physics and the Philosophical Tradition, MIT Press 1968
• H. Margeneau, The Nature of Physical Reality, McGraw-Hill 1950
• M. Chown, Forever Quantum, New Scientist No. 2595 (2007) 37.
• T. Schürmann, A Single Particle Uncertainty Relation, Acta Physica Polonica B39 (2008) 587. [18]

External links

• Copenhagen Interpretation (Stanford Encyclopedia of Philosophy)
• Physics FAQ section about Bell's inequality
• The Copenhagen Interpretation of Quantum Mechanics
• Preprint of Afshar Experiment

Category:Fundamental physics concepts Category:Interpretations of quantum mechanics Category:Quantum measurement Category:University of Copenhagen pt:Interpretação de Copenhaga

Predefinição:Cleanup-rewrite

The Bohm or Bohmian interpretation of quantum mechanics, which Bohm called the causal, or later, the ontological interpretation, is an interpretation postulated by David Bohm in 1952 as an alternative to the standard Copenhagen interpretation. The Bohm interpretation grew out of the search for an alternative model based on the assumption of hidden variables. Its basic formalism corresponds in the main to Louis de Broglie's pilot-wave theory of 1927. Consequently it is sometimes called the de Broglie-Bohm theory. The interpretation was developed further during the sixties and seventies under the heading of the causal interpretation in order to distinguish it from the purely probabilistic approach of the standard interpretation. Bohm later extended the approach to include both a deterministic and a stochastic version. The fullest presentation is given in Bohm and Hiley The Undivided Universe, presented under the heading of an ontological interpretation to emphasize its concern with “beables” rather than with “observables,” and in contradistinction to the predominantly epistemological approach of the standard model. In its final form, building on the insights of Bell and others, the ontological interpretation is causal but non-local, and non-relativistic, while capable of being extended beyond the domain of the current quantum theory in a number of ways.

In the Bohm interpretation, every particle has a definite position and momentum at all times, but we do not usually know what they are, though we do have limited information about them. The particles are guided by the wave function, which follows the Schrödinger equation.

The Bohm interpretation is an example of a hidden variables theory. Bohm originally hoped that hidden variables could provide a local, causal, objective description that would resolve or eliminate many of the paradoxes of quantum mechanics, such as Schrödinger's cat, the measurement problem and the collapse of the wavefunction. However, Bell's theorem complicates this hope, as it demonstrates that there is no locally causal hidden variable theory that is compatible with quantum mechanics. The Bohmian interpretation is causal but not local.

The Bohm interpretation is non-relativistic.

The Bohm interpretation is an interpretation of quantum mechanics. In other words, it has not been disproven, but there are other schemes (such as the Copenhagen interpretation) that give the same theoretical predictions, so are equally confirmed by the experimental results.

The theory

Principles

The Bohm interpretation is based on these principles:

• Every particle travels in a definite path

Each particle is viewed as having a definite position and velocity at all times.

• We do not know what that path is

Measurements allow us to successively retroactively refine the bounds on the particle path at some time, but there always remains some classical uncertainty in the position and momentum (as there always is in any classical theory), which increases with time.

• The state of N particles is affected by a 3N dimensional field, which guides the motion of the particles

De Broglie called this the pilot wave; Bohm called it the ψ-field. This field has a piloting influence on the motion of the particles. The quantum potential is derived from the ψ-field.

• This 3N dimensional field satisfies the Schrödinger equation

Mathematically, the field corresponds to the wavefunction of conventional quantum mechanics, and evolves according to the Schrödinger equation. The positions of the particles do not affect the wave function.

• Each particle's momentum p is $\nabla S(x,t)$

The particles momentum can be calculated from the value of the wavefunction at the position of the particle. See the section on One-particle formalism for a discussion of the mathematics.

• The particles form a statistical ensemble, with probability density $\rho (\mathbf {x} ,t)=|\psi (\mathbf {x} ,t)|^{2}$

Although we don't know the position of any individual particle before we measure them, we find after the measurement that the statistics conform to the probability density function that is based on the wavefunction in the usual way.

In its basic form, the Bohm interpretation is non-relativistic; it does not attempt to deal with high speeds or significant gravity. There are extensions that address relativistic issues.

The Bohm interpretation is an interpretation of quantum mechanics; it was originally developed as an objective and deterministic alternative to the Copenhagen interpretation. It says that the state of the universe evolves smoothly through time, with no collapsing of wavefunctions.

The Bohm interpretation is a hidden variables theory. In other words, there is a precisely defined history of the universe; however, some of the variables that define the history are not (and cannot be) known to the observer. For that reason, there is uncertainty in what we know about the universe.

Name and evolution

The Bohm Interpretation is not a single closed theory, but is open-ended and has evolved through stages. Occasionally, to understand a paper, it is necessary to identify the stage that it refers to.

In this section, each stage is given a name and a main reference. To get an understanding of which stage a paper refers to, the name is a quick (but unreliable) clue; comparing the references gives a better understanding.

Pilot-wave theory

This was the theory which de Broglie presented at the 1927 Solvay Conference.

This stage applies to many spin-less particles, and is deterministic, but lacks an adequate theory of measurement.

De Broglie-Bohm Theory or Bohmian Mechanics

This was described by Bohm's original papers 'A Suggested Interpretation of the Quantum Theory in Terms of "Hidden Variables" I and II' [Bohm 1952]. It extended the original Pilot Wave Theory to incorporate a consistent theory of measurement, and to address a criticism of Pauli that de Broglie did not properly respond to; it is taken to be deterministic (though Bohm hinted in the original papers that there should be disturbances to this, in the way Brownian motion disturbs Newtonian mechanics). This stage is known as the de Broglie-Bohm Theory in Bell's work [Bell 1987] and is the basis for 'The Quantum Theory of Motion' [Holland 1993]. It is also referred to in some papers as Bohmian Mechanics.

This stage applies to multiple particles, and is considered by most authors to be deterministic.

Causal Interpretation and Ontological Interpretation

Bohm developed his original ideas, calling them the Causal Interpretation. Later he felt that causal sounded too much like deterministic and preferred to call his theory the Ontological Interpretation. The main reference is 'The Undivided Universe' [Bohm, Hiley 1993].

These stages cover work by Bohm and in collaboration with Vigier and Hiley. Bohm is clear that this theory is non-deterministic (the work with Hiley includes a stochastic theory).

As an example, take the paper "A first experimental test of de Broglie-Bohm theory against standard quantum mechanics" This refers to "On the Incompatibility of Standard Quantum Mechanics and the de Broglie-Bohm Theory"[19]. These papers base their argument on determinism, and refer to [Holland 1993] as the reference. One can see that they refer to the deterministic de Broglie-Bohm theory but not to Bohm's Causal interpretation.

Results

The Bohm interpretation demonstrates that some features of the Copenhagen interpretation are not essential to quantum mechanics, but are a feature of the interpretation. Some specific features are:

• wave collapse
• entanglement
• the non-existence of particles while not being observed

Examination of the Bohm interpretation has shown that nonlocality is a general feature of quantum mechanics interpretations, including the Copenhagen interpretation where it was not originally obvious.

Reformulating the Schrödinger equation

Some of Bohm's insights are based on a reformulation of the Schrödinger equation; instead of using the wavefunction $\psi (\mathbf {x} ,t)$, he solves it for the magnitude $R(\mathbf {x} ,t)$ and complex phase $S(\mathbf {x} ,t)$ of the wavefunction. This section presents the mathematics; the next section presents the insights.

The Schrödinger equation for one particle of mass m is

$i\hbar {\frac {\partial \psi (\mathbf {x} ,t)}{\partial t}}={\frac {-\hbar ^{2}}{2m}}\nabla ^{2}\psi (\mathbf {x} ,t)+V(\mathbf {x} )\psi (\mathbf {x} ,t)$,

where the wavefunction $\psi (\mathbf {x} ,t)$ is a complex function of the spatial coordinate $\mathbf {x}$ and time t.

The probability density $\rho (\mathbf {x} ,t)$ is a real function defined as the magnitude of the wave function:

$\rho (\mathbf {x} ,t)=|\psi (\mathbf {x} ,t)|^{2}$.

We can express the wavefunction $\psi (\mathbf {x} ,t)$ in polar coordinates; Without loss of generality, we can define real functions $R(\mathbf {x} ,t)$ and $S(\mathbf {x} ,t)$ such that:

$\psi (\mathbf {x} ,t)=R(\mathbf {x} ,t)e^{iS(\mathbf {x} ,t)/\hbar }$.

The Schrödinger equation can then be split into two coupled equations by expressing it in terms of R and S:

${\frac {\partial R(\mathbf {x} ,t)}{\partial t}}={\frac {-1}{2m}}[R(\mathbf {x} ,t)\nabla ^{2}S(\mathbf {x} ,t)+2\nabla R(\mathbf {x} ,t)\cdot \nabla S(\mathbf {x} ,t)]$

${\frac {\partial S(\mathbf {x} ,t)}{\partial t}}=-\left[V+{\frac {1}{2m}}(\nabla S(\mathbf {x} ,t))^{2}-{\frac {\hbar ^{2}}{2m}}{\frac {\nabla ^{2}R(\mathbf {x} ,t)}{R(\mathbf {x} ,t)}}\right]$

The magnitude $R(\mathbf {x} ,t)$ is $|\psi (\mathbf {x} ,t)|$, so that $R^{2}(\mathbf {x} ,t)$ corresponds to the probability density $\rho (\mathbf {x} ,t)=|\psi (\mathbf {x} ,t)|^{2}$.

$S(\mathbf {x} ,t)$ is the complex phase chosen to have the units and typical variable name of an action. Thus

$\psi (\mathbf {x} ,t)={\sqrt {\rho (\mathbf {x} ,t)}}e^{iS(\mathbf {x} ,t)/\hbar }$.

Therefore we can substitute $\rho (\mathbf {x} ,t)$ for $R^{2}(\mathbf {x} ,t)$ and get:

$-{\frac {\partial \rho (\mathbf {x} ,t)}{\partial t}}=\nabla \cdot \left(\rho (\mathbf {x} ,t){\frac {\nabla S(\mathbf {x} ,t)}{m}}\right)\qquad (1)$

$-{\frac {\partial S(\mathbf {x} ,t)}{\partial t}}=V(\mathbf {x} )+Q(\mathbf {x} ,t)+{\frac {1}{2m}}(\nabla S(\mathbf {x} ,t))^{2}\qquad (2)$

where

$Q(\mathbf {x} ,t)=-{\frac {\hbar ^{2}}{2m}}{\frac {\nabla ^{2}R(\mathbf {x} ,t)}{R(\mathbf {x} ,t)}}=-{\frac {\hbar ^{2}}{2m}}{\frac {\nabla ^{2}{\sqrt {\rho (\mathbf {x} ,t)}}}{\sqrt {\rho (\mathbf {x} ,t)}}}=-{\frac {\hbar ^{2}}{2m}}\left({\frac {\nabla ^{2}\rho (\mathbf {x} ,t)}{2\rho (\mathbf {x} ,t)}}-\left({\frac {\nabla \rho (\mathbf {x} ,t)}{2\rho (\mathbf {x} ,t)}}\right)^{2}\right)$

Bohm called the function $Q(\mathbf {x} ,t)$ the quantum potential.

We can use the same argument on the many-particle Schrödinger equation:

$i\hbar {\frac {\partial \psi (\mathbf {x_{1},x_{2},...} ,t)}{\partial t}}=\sum _{i}{\frac {-\hbar ^{2}}{2m_{i}}}\nabla _{i}^{2}\psi (\mathbf {x_{1},x_{2},..} ,t)+V(\mathbf {x_{1},x_{2},..} )\psi (\mathbf {x_{1},x_{2},...} ,t)$,

where the i-th particle has mass $m_{i}\,$ and position coordinate $\mathbf {x_{i}}$ at time t. The wavefunction $\psi (\mathbf {x_{1},x_{2},...} ,t)$ is a complex function of all the $\mathbf {x_{i}}$ and time t. $\nabla _{i}$ is the grad operator with respect to $\mathbf {x_{i}}$, i.e. of the i-th particle's position coordinate. As before the probability density $\rho (\mathbf {x_{1},x_{2},...} ,t)$ is a real function defined by

$\rho (\mathbf {x_{1},x_{2},..} ,t)=|\psi (\mathbf {x_{1},x_{2},..} ,t)|^{2}$.

As before, we can define a real function $S(\mathbf {x_{1},x_{2},...} ,t)$ to be the complex phase,so that we can define a similar relationship to the 1-particle example:

$\psi (\mathbf {x_{1},x_{2},..} ,t)={\sqrt {\rho (\mathbf {x_{1},x_{2},..} ,t)}}e^{iS(\mathbf {x_{1},x_{2},..} ,t)/\hbar }$.

We can use the same argument to express the Schrödinger equation in terms of $\rho (\mathbf {x_{1},x_{2},..} ,t)$ and $S(\mathbf {x_{1},x_{2},..} ,t)$:

$-{\frac {\partial \rho (\mathbf {x_{1},x_{2},..} ,t)}{\partial t}}=\sum _{i}\nabla _{i}\cdot (\rho (\mathbf {x_{1},x_{2},..} ,t){\frac {\nabla _{i}S(\mathbf {x_{1},x_{2},..} ,t)}{m_{i}}})\qquad (3)$

$-{\frac {\partial S(\mathbf {x_{1},x_{2},..} ,t)}{\partial t}}=V(\mathbf {x_{1},x_{2},..} )+Q(\mathbf {x_{1},x_{2},..} ,t)+\sum _{i}{\frac {1}{2m_{i}}}(\nabla _{i}S(\mathbf {x_{1},x_{2},..} ,t))^{2}\qquad (4)$

where

$Q(\mathbf {x_{1},x_{2},..} ,t)=-\sum _{i}{\frac {\hbar ^{2}}{2m_{i}}}{\frac {\nabla _{i}^{2}R(\mathbf {x_{1},x_{2},..} ,t)}{R(\mathbf {x_{1},x_{2},..} ,t)}}=-\sum _{i}{\frac {\hbar ^{2}}{2m_{i}}}\left({\frac {\nabla _{i}^{2}\rho (\mathbf {x_{1},x_{2},..} ,t)}{2\rho (\mathbf {x_{1},x_{2},..} ,t)}}-\left({\frac {\nabla _{i}\rho (\mathbf {x_{1},x_{2},..} ,t)}{2\rho (\mathbf {x_{1},x_{2},..} ,t)}}\right)^{2}\right)$.

One-particle formalism

In his 1952 paper, Bohm starts from the reformulated Schrödinger equation. He points out that in equation (2):

$-{\frac {\partial S(\mathbf {x} ,t)}{\partial t}}=V(\mathbf {x} )+Q(\mathbf {x} ,t)+{\frac {1}{2m}}(\nabla S(\mathbf {x} ,t))^{2}$,

if one represents the world of classical physics by setting $\hbar$ to zero (which results in Q becoming zero) then $S(\mathbf {x} ,t)$ is the solution to the Hamilton-Jacobi equation. He quotes a theorem that says that if an ensemble of particles (which follow the equations of motion) have trajectories that are normal to a surface of constant S, then they are normal to all surfaces of constant S, and that $\nabla S(\mathbf {x} ,t)/m$ is the velocity of any particle passing point $\mathbf {x}$ at time t.

Therefore, we can express equation (1) as:

$-{\frac {\partial \rho (\mathbf {x} ,t)}{\partial t}}=\nabla \cdot \left(\rho (\mathbf {x} ,t)\mathbf {v} \right)$

This equation shows that it is consistent to express $\rho (\mathbf {x} ,t)$ as the probability density because $\rho (\mathbf {x} ,t)\mathbf {v}$ is then the mean current of particles, and the equation expresses the conservation of probability.

Of course, $\hbar$ is non-zero. Bohm suggests that we still treat the particle velocity as $\nabla S(\mathbf {x} ,t)/m$. The movement of a particle is described by equation (2):

$-{\frac {\partial S(\mathbf {x} ,t)}{\partial t}}=V(\mathbf {x} )+Q(\mathbf {x} ,t)+{\frac {1}{2m}}(\nabla S(\mathbf {x} ,t))^{2}$

where

$Q(\mathbf {x} ,t)=-{\frac {\hbar ^{2}}{2m}}\left({\frac {\nabla ^{2}\rho (\mathbf {x} ,t)}{2\rho (\mathbf {x} ,t)}}-\left({\frac {\nabla \rho (\mathbf {x} ,t)}{2\rho (\mathbf {x} ,t)}}\right)^{2}\right)$

V is the classical potential, which influences the particle's movement in the ways described by the classical laws of motion.

Q also has the form of a potential; it is known as the quantum potential. It influences particles in ways that are specific to quantum theory. Thus the particle is moving under the influence of a quantum potential Q as well as the classical potential V.

The quantum potential does not vary with the strength of the ψ-field; this is evident because ρ and its derivatives appear both in the numerator and the denominator of the quantum potential. Thus the quantum potential guides the particles, even when the ψ-field is weak.

Many-particle formalism

The momentum of Bohm's i-th particle's "hidden variable" is defined by

$\mathbf {p_{i}} ={m_{i}}\mathbf {v_{i}} =\nabla _{i}S\qquad (3)$

and the particles' total energy as $E=-\partial S/\partial t$; equation (1) is the continuity equation for probability with

$\mathbf {j_{i}} =\rho \mathbf {v_{i}} =\rho {\frac {\mathbf {p_{i}} }{m_{i}}}=\rho {\frac {\nabla _{i}S}{m_{i}}}$,

and equation (4) is a statement that total energy is the sum of the potential energy, quantum potential and the kinetic energies.

Comparison with experimental data

An important prediction of the Bohm theory, made in Bohm's original 1952 paper, is that the electron in the ground state of a hydrogen atom is at rest (cf. equation (3) above - s states have spherical symmetry and thus have constant phase), as the quantum force introduced by Bohm balances the classical electromagnetic potential.

Any measurement of the momentum of a ground state electron will give a non-zero result as predicted by quantum mechanics, but Bohm's theory argues that the act of measuring the momentum disturbs the electron at rest, resulting in a non-zero expection value.

Experimental observation of the decay rates of muons bound in exotic atoms has shown, however, that ground state electrons are in fact in motion. Because of their mass, muons captured in higher states rapidly cascade to the ground state, and about 99 percent of the bound muons decay from the 1S state. If the atomic number of the hydrogen-like atom is high enough, the muon motion will be relativistic, and subject to time dilation. The data show that for moderate Z atoms, the observed lengthening of the muon decay time can be attributed to the relativistic time dilation.

Since the motion of the muon has been demonstrated without any disturbance of the atom, it cannot be explained by disturbances related to the measurement process as with conventional measurements of the momentum of ground state electrons. An important conceptual prediction of the Bohm model, namely that ground state electrons are at rest, would seem to be contradicted by experimental evidence. But Bohm's prediction of the lack of motion of the lepton in the s state is only a non-relativistic prediction, since the Schrödinger equation is non-relativistic. Therefore the muon result, which relies on time dilation, is not at variance with the accepted theoretical demonstration that Bohm's theory reproduces all the non-relativistic results of the other conventional quantum interpretations.

Further, it should be noted that since relativistic quantum theories (such as quantum field theory) can always be expressed in terms of a local Lagrangian density, it follows that probability mass in such theories always flows locally through configuration space, and therefore that a classical configuration of the system's (field) variables can still be made to evolve locally in a way that simply tracks the flow of the conserved probability current in configuration space. Therefore, Bohm's interpretation can be extended to a relativistic version that works in such a way that it exactly duplicates the predictions of standard quantum field theory, so, in fact, there can be no experimental contradiction of Bohm's approach (if suitably generalized in this way) that does not also contradict the standard model.{{carece de fontes}}

Understanding quantum mechanics

Indeterminism in the Bohm Interpretation.

A major difference between Bohm’s interpretation and the usual one is the approach to the indeterminism. In the usual interpretation, the Schrödinger equation is treated not as an actual field, but as a probability density matrix (Born) which yields the resultant statistical data. According to the founding fathers, there is no way to produce results which would be more exact by referring to any “hidden variables” beyond the theory itself. Thus, in the usual interpretation, there is what Bohm calls an “irreducible lawlessness” which goes beyond our lack of knowledge or coarse graining.

For Bohm, on the other hand, the indeterminism implied by the theory is only at the level of the macroscopic experimental apparatus (e.g. the observables), and is not part of the nature of reality. Bohm expected that the underlying motions of a sub-quantum domain could be more precisely defined than allowed by the standard model, so that the degrees of freedom implied are considerably reduced.

Heisenberg's uncertainty principle

The Heisenberg uncertainty principle states that when two complementary measurements are made, there is a limit to the product of their accuracy. As an example, if one measures the position with an accuracy of $\Delta x$, and the momentum with an accuracy of $\Delta p$, then $\Delta x\Delta p\gtrsim h.$ If we make further measurements in order to get more information, we disturb the system and change the trajectory into a new one depending on the measurement set up; therefore, the measurement results are still subject to Heisenberg's uncertainty relation.

In Bohm's interpretation, there is no uncertainty in position and momentum of a particle; therefore a well defined trajectory is possible, but we have limited knowledge of what this trajectory is (and thus of the position and momentum). It is our knowledge of the particle's trajectory that is subject to the uncertainty relation. What we know about the particle is described by the same wave function that other interpretations use, so the uncertainty relation can be derived in the same way as for other interpretations of quantum mechanics.

To put the statement differently, the particles' positions are only known statistically. As in classical mechanics, successive observations of the particles' positions refine the initial conditions. Thus, with succeeding observations, the initial conditions become more and more restricted. This formalism is consistent with normal use of the Schrödinger equation. It is the underlying chaotic behaviour of the hidden variables that allows the defined positions of the Bohm theory to generate the apparent indeterminacy associated with each measurement, and hence recover the Heisenberg uncertainty principle.

For the derivation of the uncertainty relation, see Heisenberg uncertainty principle, noting that it describes it from the viewpoint of the Copenhagen interpretation.

Two-slit experiment

The double-slit experiment is an illustration of wave-particle duality. In it, a beam of particles (such as photons) travels through a barrier with two slits removed. If one puts a detector screen on the other side, the pattern of detected particles shows interference fringes characteristic of waves; however, the detector screen responds to particles. The photons must exhibit behaviour of both waves and particles.

The Copenhagen interpretation requires that the photons are not localised in space until they are detected, and travel through both slits.

In the Bohm interpretation, the guiding wave travels through both slits and sets up a ψ-field; the initial positions of the photons are not known to the observer, but they travel under the guidance of the ψ-field. Each photon that is detected has travelled through one of the slits; together, their statistics show the probability distribution of the ψ-field, which gives interference fringes that are characteristic of waves. The photons are localized particles at all times, and hence are able to activate the detector screen.

Measuring spin and polarization

It is not possible to measure the spin or polarization of a particle directly; instead, the component in one direction is measured; the outcome from a single particle may be 1, meaning that the particle is aligned with the measuring apparatus, or -1, meaning that it is aligned the opposite way. For an ensemble of particles, if we expect the particles to be aligned, the results are all 1. If we expect them to be aligned oppositely, the results are all -1. For other alignments, we expect some results to be 1 and some to be -1 with a probability that depends on the expected alignment. For a full explanation of this, see the Stern-Gerlach Experiment.

In the Bohm interpretation, we calculate the wave function that corresponds to the setup of the apparatus (including the orientation of the detectors); the particles are guided by this function, so we can calculate the probabilities that the actual particles will reach each part of the detector apparatus.

The Einstein-Podolsky-Rosen paradox

In the Einstein-Podolsky-Rosen paradox, the authors point out that it is possible to create pairs of particles with quantum states that are mirror-images of each other; these particles are now described as entangled. They describe a thought-experiment showing that either quantum mechanics is an incomplete theory or that it has nonlocality.

John Bell then described Bell's theorem (see p.14 in), in which he shows that all hidden-variable theories (including the Bohm interpretation) have nonlocality. Bell went further, showing that quantum mechanics itself is nonlocal and that this cannot be avoided by appealing to any alternative interpretation (p. 196 in): "It is known that with Bohm's example of EPR correlations, involving particles with spin, there is an irreducible nonlocality."

Alain Aspect took this further by creating Bell test experiments, which realize the thought experiments on which Bell's theorem is based. He was able to show experimentally that Bell's results hold.

In the Bell test experiment, entangled pairs of particles are created; the particles are separated, travelling to remote measuring apparatus. The orientation of the measuring apparatus can be changed while the particles are in flight, demonstrating the non-locality of the effect. The apparatus makes a statistical detection of the orientation of the particles (see Measuring spin and polarization for a description of this). Bell's Theorem shows that the results at each detector depend on the orientation of both detectors.

The Bohm interpretation describes this experiment as follows: to understand the evolution of these particles, we need to set up a wave equation for both particles; the orientation of the apparatus affects the wave function. The particles in the experiment follow the guidance of the wave function; we don't know the initial conditions of these particles, but we can predict the statistical outcome of the experiment from the wave function. It is the wave function that carries the faster-than-light effect of changing the orientation of the apparatus.

History

Bohm became dissatisfied with the conventional interpretation of quantum mechanics, pointing out that, although it requires one to give up "the possibility of even conceiving what might determine the behaviour of an individual system at a quantum level", it doesn't prove that this requirement is necessary.

To highlight this, Bohm published 'A Suggested Interpretation of Quantum Mechanics in Terms of "Hidden" Variables' [Bohm 1952]. In this paper, Bohm presented his alternative.

While preparing this paper, Bohm became aware of de Broglie's Pilot wave theory. This was a hidden-variable theory which de Broglie presented at the 1927 Solvay Conference. At the conference, Wolfgang Pauli pointed out that it did not deal properly with the case of inelastic scattering. De Broglie was persuaded by this argument, and abandoned this theory. Later, in 1932, John von Neumann published a paper, claiming to prove that all hidden-variable theories are impossible. This clearly applied to both de Broglie's and Bohm's theories.

Bohm's paper was largely ignored by other physicists; surprisingly, it was not supported by Albert Einstein (who was also dissatisfied with the prevailing orthodoxy and had discussed Bohm's ideas with him before publication). So Bohm lost interest in it.

The cause was taken up by John Bell. In "Speakable and Unspeakable in Quantum Mechanics" [Bell 1987], several of the papers refer to hidden variables theories (which include Bohm's). Bell showed that Pauli's and von Neumann's objections amounted to showing that hidden variables theories are nonlocal, and that nonlocality is a feature of all quantum mechanical systems.

The Bohm interpretation is now considered by some to be a valid challenge to the prevailing orthodoxy of the Copenhagen Interpretation, but it remains controversial.

Extensions

Exploiting Nonlocality

Antony Valentini of the Perimeter Institute has extended the Bohm Interpretation to include signal nonlocality that would allow entanglement to be used as a stand-alone communication channel without a secondary classical "key" signal to "unlock" the message encoded in the entanglement. This violates orthodox quantum theory but it has the virtue that it makes the parallel universes of the chaotic inflation theory observable in principle.

Valentini cites earlier work that shows that orthodox quantum theory corresponds to "sub-quantal thermal equilibrium" for the hidden variables.

The larger theory is a non-equilibrium theory: in Bohm's ontology, the hidden variable "particles" and "field configurations" receive their marching orders from the ψ-wave, but do not directly react back on it (see Ch 14 of the "Undivided Universe"); in Valentini's theory, this direct feedback of particle on its guiding pilot wave introduces an instability, a feedback loop that pushes the hidden variables out of thermal equilibrium "sub-quantal heat death" (Valentini). The resulting theory becomes nonlinear and non-unitary. The Born probability interpretation can no longer be sustained in this emergence of new order in complex systems that P.W. Anderson has called "More is different."

Isomorphism to the many worlds interpretation

Explicitly non-local. Bohm accepts that all the branches of the universal wavefunction exist. Like Everett, Bohm held that the wavefunction is real complex-valued field which never collapses. In addition Bohm postulated that there were particles that move under the influence of a non-local "quantum- potential" derived from the wavefunction (in addition to the classical potentials which are already incorporated into the structure of the wavefunction). The action of the quantum- potential is such that the particles are affected by only one of the branches of the wavefunction. (Bohm derives what is essentially a decoherence argument to show this, see section 7,#I [B]).

The implicit, unstated assumption made by Bohm is that only the single branch of wavefunction associated with particles can contain self-aware observers, whereas Everett makes no such assumption. Most of Bohm's adherents do not seem to understand (or even be aware of) Everett's criticism, section VI [1], that the hidden- variable particles are not observable since the wavefunction alone is sufficient to account for all observations and hence a model of reality. The hidden variable particles can be discarded, along with the guiding quantum-potential, yielding a theory isomorphic to many-worlds, without affecting any experimental results.

Quantum trajectory method

Work by Robert Wyatt in the early 2000s attempted to use the Bohm "particles" as an adaptive mesh that follows the actual trajectory of a quantum state in time and space. In the "quantum trajectory" method, one samples the quantum wave function with a mesh of quadrature points. One then evolves the quadrature points in time according to the Bohm equations of motion. At each time-step, one then re-synthesizes the wave function from the points, recomputes the quantum forces, and continues the calculation. (Quick-time movies of this for H+H₂ reactive scattering can be found on the Wyatt group web-site at UT Austin.) This approach has been adapted, extended, and used by a number of researchers in the Chemical Physics community as a way to compute semi-classical and quasi-classical molecular dynamics. A recent issue of the Journal of Physical Chemistry A was dedicated to Prof. Wyatt and his work on "Computational Bohmian Dynamics".

Eric Bittner's group at the University of Houston has advanced a statistical variant of this approach that uses Bayesian sampling technique to sample the quantum density and compute the quantum potential on a structureless mesh of points. This technique was recently used to estimate quantum effects in the heat-capacity of small clusters Ne_n for n~100.

There remain difficulties using the Bohmian approach, mostly associated with the formation of singularities in the quantum potential due to nodes in the quantum wave function. In general, nodes forming due to interference effects lead to the case where ${\frac {1}{R}}\nabla ^{2}R\rightarrow \infty .$ This results in an infinite force on the sample particles forcing them to move away from the node and often crossing the path of other sample points (which violates single-valuedness). Various schemes have been developed to overcome this; however, no general solution has yet emerged.

There has also been recent work in developing Complex Bohmian trajectories which satisfy isochronal relations.

Quantum chaos

There are developments in quantum chaos. In this theory, there exist quantum wave functions that are fractal and thus differentiable nowhere. While such wave functions can be solutions of the Schrödinger equation, taken in its entirety, they would not be solutions of Bohm's coupled equations for the polar decomposition of ψ into ρ and S, (see Reformulating the Schrödinger equation). The breakdown occurs when expressions involving ρ or S become infinite (due to the non-differentiability), even though the average energy of the system stays finite, and the time-evolution operator stays unitary. Desde 2005, it does not appear that experimental tests of this nature have been performed.

Other extensions

The theory can also easily be extended to include spin, as well as the relativistic Dirac theory. In the latter case, such relativistic extensions inherently involve an experimentally unobservable preferred frame, and this is considered by many to be in tension with the "spirit" of special relativity.

As probability density and probability current can be defined for any set of commuting operators, the Bohmian formalism is not limited to the position operator.

Frequently asked questions

Q: Why should we consider this to be a separate theory when it looks contrived, and gives the same measurable predictions as conventional quantum mechanics?

A: Bohm's original aim was to demonstrate that hidden-variables theories are possible, and his hope was that this demonstration could lead to new insights, measurable predictions and experiments. So far, the Bohm interpretation has had these results:

• it has shown that a hidden-variable theory is possible; this has highlighted that some parts of other interpretations (such as wave collapse) are part of the interpretation and not an inevitable part of physics.
• it has highlighted the issue of nonlocality: it inspired John Stewart Bell to prove his now-famous theorem, which in turn led to the Bell test experiments. These showed that all theories of quantum mechanics must address nonlocality.

Q: While orthodox quantum mechanics admits many observables on the Hilbert space that are treated almost equivalently (much like the bases composed of their eigenvectors), Bohm's interpretation requires one to pick a set of "privileged" observables that are treated classically — namely the position. How can this be justified, when there is no experimental reason to think that some observables are fundamentally different from others?

A: Positions may be considered as a natural choice for the selection because positions are most directly measurable. For example, one does not actually measure the "spin" of a particle in the Stern–Gerlach experiment, but instead measures the position of the light flashes on a detector. Often the observed quantities are positions, e.g. of a measuring needle or of the particles making up a computer display. Thus there is justification for making position privileged.

Q: The Bohmian models are nonlocal; how can this be reconciled with the principles of special relativity? they make it highly nontrivial to reconcile the Bohmian models with up-to-date models of particle physics, such as quantum field theory or string theory, and with some very accurate experimental tests of special relativity, without some additional explanation. On the other hand, other interpretations of quantum mechanics, such as consistent histories or the many-worlds interpretation, allow us to explain the experimental tests of quantum entanglement without any nonlocality whatsoever.

A: It is questionable whether other interpretations of quantum theory are local or are simply less explicit about nonlocality. See for example the EPR type of nonlocality. And recent tests of Bell's Theorem add weight to the belief that all quantum theories must abandon either the principle of locality or counterfactual definiteness (the ability to speak meaningfully about the definiteness of the results of measurements, even if they were not performed).

Finding a Lorentz-invariant expression of the Bohm interpretation (or any nonlocal hidden-variable theory) has proved difficult, and it remains an open question for physicists today whether such a theory is possible and how it would be achieved.

There has been work in this area. See Bohm and Hiley: The Undivided Universe, and [20], [21], and references therein. Also [22] and [23] for a quantum field theory treatment.

Q: The wavefunction must "disappear" or "collapse" after a measurement, and this process seems highly unnatural in the Bohmian models. The Bohmian interpretation also seems incompatible with modern insights about decoherence that allow one to calculate the "boundary" between the "quantum microworld" and the "classical macroworld"; according to decoherence, the observables that exhibit classical behavior are determined dynamically, not by an assumption.

A: Collapse is a main feature of von Neumann's theory of quantum measurement. In the Bohm interpretation, a wave does not collapse; instead, a measurement produces what Bohm called "empty channels" consisting of portions of the wave that no longer affect the particle. This conforms to the principle of decoherence, where a quantum system interacts with its environment to give the appearance of wavefunction collapse. The Bohm interpretation does not require a boundary between a quantum system and its classical environment.

Q: The Bohm interpretation involves reverse-engineering of quantum potentials and trajectories from standard QM. Diagrams in Bohm's book are constructed by forming contours on standard QM interference patterns and are not calculated from his "mathematical" formulation. Recent experiments with photons arXiv:quant-ph/0206196 v1 28 Jun 2002 favor standard QM over Bohm's trajectories.

A: The Bohm interpretation takes the Schrödinger equation even more seriously than does the conventional interpretation. In the Bohm interpretation, the quantum potential is a quantity derived from the Schrödinger equation, not a fundamental quantity. Thus, the interference patterns in the Bohm interpretation are identical to those in the conventional interpretation. As shown in [24] and [25], the experiments cited above only disprove a misinterpretation of the Bohm interpretation, not the Bohm interpretation itself.

Q: Hugh Everett says that Bohm's particles are not observable entities, but surely they are - what hits the detectors and causes flashes?

A: Both Everett and Bohm treat the wavefunction as a complex-valued but real field. Everett's Many-worlds interpretation is an attempt to demonstrate that the wavefunction alone is sufficient to account for all our observations. When we see the particle detectors flash or hear the click of a Geiger counter or whatever then Everett interprets this as our wavefunction responding to changes in the detector's wavefunction, which is responding in turn to the passage of another wavefunction (which we think of as a "particle", but is actually just another wave-packet). But no particle in the Bohm sense of having a defined position and velocity is involved. For this reason Everett sometimes referred to his approach as the "wave interpretation". Talking of Bohm's approach, Everett says:

“ Our main criticism of this view is on the grounds of simplicity - if one desires to hold the view that $\psi$ is a real field then the associated particle is superfluous since, as we have endeavored to illustrate, the pure wave theory is itself satisfactory. ”

In this view, then, the Bohm particles are unobservable entities, similar to and equally as unnecessary as, for example, the luminiferous ether was found to be unnecessary in special relativity. We can remove the particles from Bohm's theory and still account for all our observations. The unobservability of the "hidden particles" stems from an asymmetry in the causal structure of the theory; the wavefunction influences the position and velocity of the hidden variables (i.e. the particles are influenced by a "force" exerted by the wavefunction), but the hidden variables do not influence the time development of the wavefunction (i.e. there is no analogue of Newton's third law -- the particles do not react back onto the wavefunction). Thus the particles do not make their presence known in any way; as the theory says, they are hidden.

See also

• David Bohm
• Holomovement
• Holonomic brain theory
• Implicate and Explicate Order
• Interpretation of quantum mechanics
• Local hidden variable theory
• Quantum mechanics
• Quantum consciousness
• Dark energy
• Pilot wave

External links

• "Bohmian Mechanics" (Stanford Encyclopedia of Philosophy)
• "Pilot waves, Bohmian metaphysics, and the foundations of quantum mechanics", lecture course on Bohm interpretation by Mike Towler, Cambridge University.

Category:Interpretations of quantum mechanics Category:Quantum measurement pt:Interpretação de Bohm

Predefinição:Quantum mechanics The Pauli exclusion principle is a quantum mechanical principle formulated by Wolfgang Pauli in 1925. It states that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement of this principle is that, for two identical fermions, the total wave function is anti-symmetric. For electrons in a single atom, it states that no two electrons can have the same four quantum numbers, that is, if n, l, and m_l are the same, m_s must be different such that the electrons have opposite spins.

In relativistic quantum field theory, the Pauli principle follows from applying a rotation operator in imaginary time to particles of half-integer spin. It does not follow from any spin relation in nonrelativistic quantum mechanics.{{carece de fontes}}

Overview

The Pauli exclusion principle is one of the most important principles in physics, mainly because the three types of particles from which ordinary matter is made—electrons, protons, and neutrons—are all subject to it; consequently, all material particles exhibit space-occupying behavior. The Pauli exclusion principle underpins many of the characteristic properties of matter from the large-scale stability of matter to the existence of the periodic table of the elements. Particles with antisymmetric wave functions are called fermions—and obey the Pauli exclusion principle. Apart from the familiar electron, proton and neutron, these include neutrinos and quarks (from which protons and neutrons are made), as well as some atoms like helium-3. All fermions possess "half-integer spin", meaning that they possess an intrinsic angular momentum whose value is $\hbar =h/2\pi$ (Planck's constant divided by 2π) times a half-integer (1/2, 3/2, 5/2, etc.). In the theory of quantum mechanics, fermions are described by "antisymmetric states", which are explained in greater detail in the article on identical particles. Particles with integer spin have a symmetric wave function and are called bosons; in contrast to fermions, they may share the same quantum states. Examples of bosons include the photon, the Cooper pairs responsible for superconductivity, and the W and Z bosons.

History

In the early 20th century, it became evident that atoms and molecules with pairs of electrons or even numbers of electrons are more stable than those with odd numbers of electrons. In the famous 1916 article The Atom and the Molecule by Gilbert N. Lewis, for example, rule three of his six postulates of chemical behavior states that the atom tends to hold an even number of electrons in the shell and especially to hold eight electrons which are normally arranged symmetrically at the eight corners of a cube (see: cubical atom). In 1919, the American chemist Irving Langmuir suggested that the periodic table could be explained if the electrons in an atom were connected or clustered in some manner. Groups of electrons were thought to occupy a set of electron shells about the nucleus. In 1922, Niels Bohr updated his model of the atom by assuming that certain numbers of electrons (for example 2, 8 and 18) corresponded to stable "closed shells".

Pauli looked for an explanation for these numbers which were at first only empirical. At the same time he was trying to explain experimental results in the Zeeman effect in atomic spectroscopy and in ferromagnetism. He found an essential clue in a 1924 paper by E.C.Stoner which pointed out that for a given value of the principal quantum number (n), the number of energy levels of a single electron in the alkali metal spectra in an external magnetic field, where all degenerate energy levels are separated, is equal to the number of electrons in the closed shell of the rare gases for the same value of n. This led Pauli to realize that the complicated numbers of electrons in closed shells can be reduced to the simple rule one per state, if the electron states are defined using four quantum numbers. For this purpose he introduced a new two-valued quantum number, identified by Samuel Goudsmit and George Uhlenbeck as electron spin.

Connection to quantum state symmetry

The Pauli exclusion principle with a single-valued many-particle wavefunction is equivalent to the assumption that the wavefunction is antisymmetric. An antisymmetric two-particle state is represented as a sum of states in which one particle is in state $\scriptstyle |x\rangle$ and the other in state $\scriptstyle |y\rangle$:

$|\psi \rangle =\sum _{xy}A(x,y)|x,y\rangle$

and antisymmetry under exchange means that A(x,y) = -A(y,x). This implies that A(x,x)=0, which is Pauli exclusion. It is true in any basis, since unitary changes of basis keep antisymmetric matrices antisymmetric, although strictly speaking, the quantity A(x,y) is not a matrix but an antisymmetric rank two tensor.

Conversely, if the diagonal quantities A(x,x) are zero in every basis, then the wavefunction component:

$A(x,y)=\langle \psi |x,y\rangle =\langle \psi |(|x\rangle \otimes |y\rangle )$

is necessarily antisymmetric. To prove it, consider the matrix element:

$\langle \psi |((|x\rangle +|y\rangle )\otimes (|x\rangle +|y\rangle ))\,$

This is zero, because the two particles have zero probability to both be in the superposition state $\scriptstyle |x\rangle +|y\rangle$. But this is equal to

$\langle \psi |x,x\rangle +\langle \psi |x,y\rangle +\langle \psi |y,x\rangle +\langle \psi |y,y\rangle \,$

The first and last terms on the right hand side are diagonal elements and are zero, and the whole sum is equal to zero. So the wavefunction matrix elements obey:

$\langle \psi |x,y\rangle +\langle \psi |y,x\rangle =0\,$.

or

$A(x,y)=-A(y,x)\,$

According to the spin-statistics theorem, particles with integer spin occupy symmetric quantum states, and particles with half-integer spin occupy antisymmetric states; furthermore, only integer or half-integer values of spin are allowed by the principles of quantum mechanics.

Consequences

Atoms and the Pauli principle

The Pauli exclusion principle helps explain a wide variety of physical phenomena. One such consequence of the principle is the elaborate electron shell structure of atoms and of the way atoms share electron(s) - thus variety of chemical elements and of their combinations (chemistry). (An electrically neutral atom contains bound electrons equal in number to the protons in the nucleus. Since electrons are fermions, the Pauli exclusion principle forbids them from occupying the same quantum state, so electrons have to "pile on top of each other" within an atom).

For example, consider a neutral helium atom, which has two bound electrons. Both of these electrons can occupy the lowest-energy (1s) states by acquiring opposite spin. This does not violate the Pauli principle because spin is part of the quantum state of the electron, so the two electrons are occupying different quantum states. However, the spin can take only two different values (or eigenvalues). In a lithium atom, which contains three bound electrons, the third electron cannot fit into a 1s state, and has to occupy one of the higher-energy 2s states instead. Similarly, successive elements produce successively higher-energy shells. The chemical properties of an element largely depend on the number of electrons in the outermost shell, which gives rise to the periodic table of the elements.

Solid state properties and the Pauli principle

In conductors and semi-conductors free electrons have to share entire bulk space - thus their energy levels stack up creating band structure out of each atomic energy level. In strong conductors (metals) electrons are so degenerate that they can not even contribute much into thermal capacity of a metal. Many mechanical, electrical, magnetic, optical and chemical properties of solids are the direct consequence of Pauli exclusion.

Stability of matter

The stability of the electrons in an atom itself is not related to the exclusion principle, but is described by the quantum theory of the atom. The underlying idea is that close approach of an electron to the nucleus of the atom necessarily increases its kinetic energy, basically an application of the uncertainty principle of Heisenberg. However, stability of large systems with many electrons and many nuclei is a different matter, and requires the Pauli exclusion principle. Some history follows.

It has been shown that the Pauli exclusion principle is responsible for the fact that ordinary bulk matter is stable and occupies volume. The first suggestion in 1931 was by Paul Ehrenfest, who pointed out that the electrons of each atom cannot all fall into the lowest-energy orbital and must occupy successively larger shells. Atoms therefore occupy a volume and cannot be squeezed too close together.

A more rigorous proof was provided by Freeman Dyson and Andrew Lenard in 1967, who considered the balance of attractive (electron-nuclear) and repulsive (electron-electron and nuclear-nuclear) forces and showed that ordinary matter would collapse and occupy a much smaller volume without the Pauli principle. The consequence of the Pauli principle here is that electrons of the same spin are kept apart by a repulsive exchange force or exchange interaction. This is a short-range force which is additional to the long-range electrostatic or coulombic force. This additional force is therefore responsible for the everyday observation in the macroscopic world that two solid objects cannot be in the same place in the same time.

Dyson and Lenard did not consider the extreme magnetic or gravitational forces which occur in some astronomical objects. In 1995 Elliott Lieb and coworkers showed that the Pauli principle still leads to stability in intense magnetic fields as in neutron stars, although at much higher density than in ordinary matter. It is postulated that in sufficiently intense gravitational fields, matter collapses to form a black hole, in apparent contradiction to the exclusion principle.

Astrophysics and the Pauli principle

Astronomy provides another spectacular demonstration of this effect, in the form of white dwarf stars and neutron stars. For both such bodies, their usual atomic structure is disrupted by large gravitational forces, leaving the constituents supported by "degeneracy pressure" alone. This exotic form of matter is known as degenerate matter. In white dwarfs, the atoms are held apart by the electron degeneracy pressure. In neutron stars, which exhibit even larger gravitational forces, the electrons have merged with the protons to form neutrons, which produce a smaller degeneracy pressure, which is why neutron stars are smaller. Neutrons are the most "rigid" objects known - their Young modulus (or more accurately, bulk modulus) is 20 orders of magnitude larger than that of diamond.

See also

• Exchange force
• Exchange interaction
• Exchange symmetry
• Hund's rule
• Fermi hole

External links

• Nobel Lecture: Exclusion Principle and Quantum Mechanics Pauli's own account of the development of the Exclusion Principle.
• The Exclusion Principle (1997), Pauli's exclusion rules vs. the Aspden exclusion rules (plus the radiation factor, Larmor radiation formula, elliptical motion, the quantum states, occupancy of electron shells, nature of ferromagnetism, ...).

Category:Fundamental physics concepts Category:Spintronics Category:Chemical bonding pt:Princípio de exclusão de Pauli

In theoretical physics, the Pilot Wave theory was the first known example of a hidden variable theory, presented by Louis de Broglie in 1927. Its more modern version, the Bohm interpretation, remains a controversial attempt to interpret quantum mechanics as a deterministic theory, avoiding troublesome notions such as instantaneous wavefunction collapse and the paradox of Schrödinger's cat.

The Pilot Wave theory

The Pilot Wave theory is one of several interpretations of Quantum Mechanics. It uses the same mathematics as other interpretations of quantum mechanics; consequently, it is also supported by the current experimental evidence to the same extent as the other interpretations.

Principles

The Pilot Wave theory is a hidden variable theory. Consequently:

• the theory has realism (meaning that its concepts exist independently of the observer);
• the theory has determinism.

The position and momentum of every particle are considered hidden variables; they are defined at all times, but not known by the observer; the initial conditions of the particles are not known accurately, so that from the point of view of the observer, there are uncertainties in the particles' states which conform to Heisenberg's Uncertainty Principle.

A collection of particles has an associated wave, which evolves according to the Schrödinger Equation. Each of the particles follows a deterministic (but probably chaotic) trajectory, which is guided by the wave function; collectively, the density of the particles conform to the magnitude of the wave function.

In common with every interpretation of quantum mechanics, this theory has nonlocality.

Consequences

The Pilot Wave Theory shows that it is possible to have a theory that is realist and deterministic, but still predicts the experimental results of Quantum Mechanics.

Mathematical foundation

To be added.

History

In his 1926 paper , Max Born suggested that the wave function of Schrodinger's wave equation represents the probability density of finding a particle.

From this idea, de Broglie developed the Pilot Wave theory, and worked out a function for the guiding wave. He presented the Pilot Wave theory at the 1927 Solvay Conference. However, Wolfgang Pauli raised an objection to it at the conference, saying that it did not deal properly with the case of inelastic scattering. De Broglie was not able to find a response to this objection, and he and Born abandoned the pilot-wave approach.

Later, in 1932, John von Neumann published a paper claiming to prove that all hidden variable theories were impossible.

One would expect that, after such a bad start, this theory would disappear without trace. However, in 1952, David Bohm became dissatisfied with the prevailing orthodoxy, and rediscovered de Broglie's Pilot Wave theory. Bohm developed the Pilot Wave Theory into what is now called the De Broglie-Bohm Theory.

The de Broglie-Bohm Theory itself might have gone unnoticed by most physicists, if it had not been championed by John Bell, who also countered the objections to it. In 1987, John Bell showed that Pauli's and von Neumann's objections really only showed that the Pilot Wave theory did not have locality; in fact, no quantum mechanics theories have locality, so these objections did not invalidate the Pilot Wave theory.

The de Broglie-Bohm theory is now considered by some to be a valid challenge to the prevailing orthodoxy of the Copenhagen Interpretation, but it remains controversial.

External links

• "Pilot waves, Bohmian metaphysics, and the foundations of quantum mechanics", lecture course on Pilot wave theory by Mike Towler, Cambridge University (2009).

Bell's theorem is a no-go theorem, loosely stating that:

No physical theory of local hidden variables can ever reproduce all of the predictions of quantum mechanics.

It is the most famous legacy of the late physicist John S. Bell. The theorem has important implications for physics itself and philosophy of science as well. Physically, Bell's theorem proves that local hidden variable theories cannot remove the statistical nature of quantum mechanics. Philosophically, Bell's theorem implies that if quantum mechanics is correct, the universe is not locally deterministic.

Overview

Illustration of Bell test for spin 1/2 particles. Source produces spin singlet pair, one particle sent to Alice another to Bob. Each performs one of the two spin measurements.

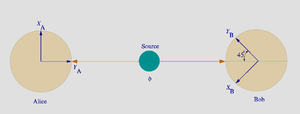
As in the situation explored in the Einstein–Podolsky–Rosen (EPR) paradox, Bell considered an experiment in which a source produces pairs of correlated particles. For example, a pair of particles with correlated spins is created; one particle is sent to Alice and the other to Bob. The experimental arrangement differs from the EPR arrangement in that a measurement is performed on both particles of a pair. On each trial, each of the observers independently chooses between various detector settings and then performs an independent measurement on the particle arriving at his position. Hence, Bell's theorem can be tested by coincidence measurements in which the correlation is measured between two independently chosen observables of the particles. (Note: although the correlated property used here is the particle's spin, it could alternatively be any correlated "quantum state" that encodes exactly one quantum bit.)

When Alice and Bob measure the spin of the particles along the same axis (but in opposite directions), they get identical results 100% of the time. But when Bob measures at orthogonal (right) angles to Alice's measurements, they get identical results only 50% of the time. In terms of mathematics, the two measurements have a correlation of 1, or perfect correlation when read the same way; when read at right angles, they have a correlation of 50% and when the angle between them is zero no correlation. (A correlation of −1 would indicate getting opposite results for each measurement.)

Same axis:	pair 1	pair 2	pair 3	pair 4	...n
Alice, 0°:	+	−	−	+	...
Bob, 180°:	+	−	−	+	...
Correlation: (	+1	+1	+1	+1	...)/n = +1
					(100% identical)
Orthogonal axes:	pair 1	pair 2	pair 3	pair 4	...n
Alice, 0°:	+	−	+	−	...
Bob, 90°:	−	−	+	+	...
Correlation: (	−1	+1	+1	−1	...)/n = 0.0
					(50% identical)

So far, the results can be explained by positing local hidden variables—each pair of particles may have been sent out with instructions on how to behave when measured in the two axes (either '+' or '−' for each axis). Clearly, if the source only sends out particles whose instructions are identical for each axis, then when Alice and Bob measure on the same axis, they are bound to get identical results, either (+, +) or (−, −); but (if all four possible pairings of + and − instructions are generated equally) when they measure on parallel axes they will see zero correlation.

Now, consider that Alice or Bob can rotate their apparatus relative to each other by any amount at any time before measuring the particles, even after the particles leave the source. If local hidden variables determine the outcome of such measurements, they must encode at the time of leaving the source a result for every possible eventual direction of measurement, not just for the results in one particular axis.

Bob begins this experiment with his apparatus rotated by 45 degrees. We call Alice's axes $a$ and $a'$, and Bob's rotated axes $b$ and $b'$. Alice and Bob then record the directions they measured the particles in, and the results they got. At the end, they will compare and tally up their results, scoring +1 for each time they got the same result and −1 for an opposite result - except that if Alice measured in a and Bob measured in $b'$, they will score +1 for an opposite result and −1 for the same result.

Using that scoring system, any possible combination of hidden variables would produce an expected average score of at most +0.5. (For example, see the table below, where the most correlated values of the hidden variables have an average correlation of +0.5; i.e. 75% identical. The unusual "scoring system" ensures that maximum average expected correlation is +0.5 for any possible system that relies on local hidden variables.)

Classical model:	highly correlated variables								less correlated variables
Hidden variable for 0° (a):	+	+	+	+	−	−	−	−	+	+	+	+	−	−	−	−
Hidden variable for 45° (b):	+	+	+	−	−	−	−	+	+	−	−	−	+	+	+	−
Hidden variable for 90° (a'):	+	+	−	−	−	−	+	+	−	+	+	−	+	−	−	+
Hidden variable for 135° (b'):	+	−	−	−	−	+	+	+	+	+	−	+	−	+	−	−
Correlation score:
If measured on a − b, score:	+1	+1	+1	−1	+1	+1	+1	−1	+1	−1	−1	−1	−1	−1	−1	+1
If measured on a' − b, score:	+1	+1	−1	+1	+1	+1	−1	+1	−1	−1	−1	+1	+1	−1	−1	−1
If measured on a' − b', score:	+1	−1	+1	+1	+1	−1	+1	+1	−1	+1	−1	−1	−1	−1	+1	−1
If measured on a − b', score:	−1	+1	+1	+1	−1	+1	+1	+1	−1	−1	+1	−1	−1	+1	−1	−1
Expected average score:	+0.5	+0.5	+0.5	+0.5	+0.5	+0.5	+0.5	+0.5	−0.5	−0.5	−0.5	−0.5	−0.5	−0.5	−0.5	−0.5

Bell's Theorem shows that if the particles behave as predicted by quantum mechanics, Alice and Bob can score higher than the classical hidden variable prediction of +0.5 correlation; if the apparatuses are rotated at 45° to each other, quantum mechanics predicts that the expected average score is 0.71.

(Quantum prediction in detail: When observations at an angle of $\theta$ are made on two entangled particles, the predicted correlation is $\cos \theta$. The correlation is equal to the length of the projection of the particle's vector onto his measurement vector; by trigonometry, $\cos \theta$. $\theta$ is 45°, and $\cos \theta$ is ${\tfrac {\sqrt {2}}{2}}$, for all pairs of axes except $(a,b')$, where they are 135° and $-{\tfrac {\sqrt {2}}{2}}$, but this last is taken in negative in the agreed scoring system, so the overall score is ${\tfrac {\sqrt {2}}{2}}$; 0.707. In one explanation, the particles behave as if when Alice or Bob makes a measurement, the other particle usually switches to take that direction instantaneously.)

Multiple researchers have performed equivalent experiments using different methods. It appears most of these experiments produce results which agree with the predictions of quantum mechanics, leading to disproof of local-hidden-variable theories and proof of nonlocality. Still, not everyone agrees with these findings. There have been two loopholes found in the earlier of these experiments, the detection loophole and the communication loophole with associated experiments to close these loopholes. After all current experimentation it seems these experiments uphold prima facie support for quantum mechanics' predictions of non-locality.

Importance of the theorem

Bell's theorem, derived in his seminal 1964 paper titled On the Einstein Podolsky Rosen paradox has been called "the most profound in science".. The title of the article refers to the famous paper by Einstein Podolsky and Rosen purporting to prove the incompleteness of quantum mechanics. In his paper, Bell started from essentially the same assumptions as did EPR, viz. i) reality (microscopic objects have real properties determining the outcomes of quantum mechanical measurements) and ii) locality (reality is not influenced by measurements simultaneously performed at a large distance). Bell was able to derive from these assumptions an important result, viz. Bell's inequality, violation of which by quantum mechanics implying that at least one of the assumptions must be abandoned if experiment would turn out to satisfy quantum mechanics. In two respects Bell's 1964 paper was a big step forward compared to the EPR paper: i) it considered more general hidden variables than the elements of physical reality of the EPR paper, ii) more importantly, Bell's inequality was liable to be experimentally tested, thus yielding the opportunity to lift the discussion on the completeness of quantum mechanics from metaphysics to physics. Whereas Bell's 1964 paper deals only with deterministic hidden variables theories, Bell's theorem was later generalized to stochastic theories as well, and it was realized that the theorem can even be proven without introducing hidden variables.

After EPR (Einstein–Podolsky–Rosen), quantum mechanics was left in an unsatisfactory position: either it was incomplete, in the sense that it failed to account for some elements of physical reality, or it violated the principle of finite propagation speed of physical effects. In a modified version of the EPR thought experiment, two observers, now commonly referred to as Alice and Bob, perform independent measurements of spin on a pair of electrons, prepared at a source in a special state called a spin singlet state. It was equivalent to the conclusion of EPR that once Alice measured spin in one direction (e.g., on the x axis), Bob's measurement in that direction was determined with certainty, with opposite outcome to that of Alice, whereas immediately before Alice's measurement, Bob's outcome was only statistically determined. Thus, either the spin in each direction is an element of physical reality, or the effects travel from Alice to Bob instantly.

In QM, predictions were formulated in terms of probabilities — for example, the probability that an electron might be detected in a particular region of space, or the probability that it would have spin up or down. The idea persisted, however, that the electron in fact has a definite position and spin, and that QM's weakness was its inability to predict those values precisely. The possibility remained that some yet unknown, but more powerful theory, such as a hidden variables theory, might be able to predict those quantities exactly, while at the same time also being in complete agreement with the probabilistic answers given by QM. If a hidden variables theory were correct, the hidden variables were not described by QM, and thus QM would be an incomplete theory.

The desire for a local realist theory was based on two assumptions:

1. Objects have a definite state that determines the values of all other measurable properties, such as position and momentum.
2. Effects of local actions, such as measurements, cannot travel faster than the speed of light (as a result of special relativity). If the observers are sufficiently far apart, a measurement taken by one has no effect on the measurement taken by the other.

In the formalization of local realism used by Bell, the predictions of theory result from the application of classical probability theory to an underlying parameter space. By a simple (but clever) argument based on classical probability, he then showed that correlations between measurements are bounded in a way that is violated by QM.

Bell's theorem seemed to put an end to local realist hopes for QM. Per Bell's theorem, either quantum mechanics or local realism is wrong. Experiments were needed to determine which is correct, but it took many years and many improvements in technology to perform them.

Bell test experiments to date overwhelmingly show that Bell inequalities are violated. These results provide empirical evidence against local realism and in favor of QM. The no-communication theorem proves that the observers cannot use the inequality violations to communicate information to each other faster than the speed of light.

John Bell's paper examines both John von Neumann's 1932 proof of the incompatibility of hidden variables with QM and the seminal paper on the subject by Albert Einstein and his colleagues.

Bell inequalities

Bell inequalities concern measurements made by observers on pairs of particles that have interacted and then separated. According to quantum mechanics they are entangled while local realism limits the correlation of subsequent measurements of the particles. Different authors subsequently derived inequalities similar to Bell´s original inequality, collectively termed Bell inequalities. All Bell inequalities describe experiments in which the predicted result assuming entanglement differs from that following from local realism. The inequalities assume that each quantum-level object has a well defined state that accounts for all its measurable properties and that distant objects do not exchange information faster than the speed of light. These well defined states are often called hidden variables, the properties that Einstein posited when he stated his famous objection to quantum mechanics: "God does not play dice."

Bell showed that under quantum mechanics, which lacks local hidden variables, the inequalities (the correlation limit) may be violated. Instead, properties of a particle are not clear to verify in quantum mechanics but may be correlated with those of another particle due to quantum entanglement, allowing their state to be well defined only after a measurement is made on either particle. That restriction agrees with the Heisenberg uncertainty principle, a fundamental and inescapable concept in quantum mechanics.

In Bell's work:

Theoretical physicists live in a classical world, looking out into a quantum-mechanical world. The latter we describe only subjectively, in terms of procedures and results in our classical domain. (...) Now nobody knows just where the boundary between the classical and the quantum domain is situated. (...) More plausible to me is that we will find that there is no boundary. The wave functions would prove to be a provisional or incomplete description of the quantum-mechanical part. It is this possibility, of a homogeneous account of the world, which is for me the chief motivation of the study of the so-called "hidden variable" possibility.

(...) A second motivation is connected with the statistical character of quantum-mechanical predictions. Once the incompleteness of the wave function description is suspected, it can be conjectured that random statistical fluctuations are determined by the extra "hidden" variables — "hidden" because at this stage we can only conjecture their existence and certainly cannot control them.

(...) A third motivation is in the peculiar character of some quantum-mechanical predictions, which seem almost to cry out for a hidden variable interpretation. This is the famous argument of Einstein, Podolsky and Rosen. (...) We will find, in fact, that no local deterministic hidden-variable theory can reproduce all the experimental predictions of quantum mechanics. This opens the possibility of bringing the question into the experimental domain, by trying to approximate as well as possible the idealized situations in which local hidden variables and quantum mechanics cannot agree

In probability theory, repeated measurements of system properties can be regarded as repeated sampling of random variables. In Bell's experiment, Alice can choose a detector setting to measure either $A(a)$ or $A(a')$ and Bob can choose a detector setting to measure either $B(b)$ or $B(b')$. Measurements of Alice and Bob may be somehow correlated with each other, but the Bell inequalities say that if the correlation stems from local random variables, there is a limit to the amount of correlation one might expect to see.

Original Bell's inequality

The original inequality that Bell derived was:

$1+\operatorname {C} (b,c)\geq |\operatorname {C} (a,b)-\operatorname {C} (a,c)|,$

where C is the "correlation" of the particle pairs and a, b and c settings of the apparatus. This inequality is not used in practice. For one thing, it is true only for genuinely "two-outcome" systems, not for the "three-outcome" ones (with possible outcomes of zero as well as +1 and −1) encountered in real experiments. For another, it applies only to a very restricted set of hidden variable theories, namely those for which the outcomes on both sides of the experiment are always exactly anticorrelated when the analysers are parallel, in agreement with the quantum mechanical prediction.

There is a simple limit of Bell's inequality which has the virtue of being completely intuitive. If the result of three different statistical coin-flips A, B, and C have the property that:

1. A and B are the same (both heads or both tails) 99% of the time
2. B and C are the same 99% of the time

then A and C are the same at least 98% of the time. The number of mismatches between A and B (1/100) plus the number of mismatches between B and C (1/100) are together the maximum possible number of mismatches between A and C.

In quantum mechanics, by letting A, B, and C be the values of the spin of two entangled particles measured relative to some axis at 0 degrees, θ degrees, and 2θ degrees respectively, the overlap of the wavefunction between the different angles is proportional to $\scriptstyle \cos(S\theta )\approx 1-S^{2}\theta ^{2}/2$. The probability that A and B give the same answer is $1-\varepsilon ^{2}$, where $\varepsilon$ is proportional to θ. This is also the probability that B and C give the same answer. But A and C are the same 1 − (2ε)² of the time. Choosing the angle so that $\epsilon =.1$, A and B are 99% correlated, B and C are 99% correlated and A and C are only 96% correlated.

Imagine that two entangled particles in a spin singlet are shot out to two distant locations, and the spins of both are measured in the direction A. The spins are 100% correlated (actually, anti-correlated but for this argument that is equivalent). The same is true if both spins are measured in directions B or C. It is safe to conclude that any hidden variables which determine the A,B, and C measurements in the two particles are 100% correlated and can be used interchangeably.

If A is measured on one particle and B on the other, the correlation between them is 99%. If B is measured on one and C on the other, the correlation is 99%. This allows us to conclude that the hidden variables determining A and B are 99% correlated and B and C are 99% correlated. But if A is measured in one particle and C in the other, the results are only 96% correlated, which is a contradiction. The intuitive formulation is due to David Mermin, while the small-angle limit is emphasized in Bell's original article.

CHSH inequality

Ver artigo principal: CHSH inequality

In addition to Bell's original inequality, the form given by John Clauser, Michael Horne, Abner Shimony and R. A. Holt, (the CHSH form) is especially important, as it gives classical limits to the expected correlation for the above experiment conducted by Alice and Bob:

$\ (1)\quad \mathbf {C} [A(a),B(b)]+\mathbf {C} [A(a),B(b')]+\mathbf {C} [A(a'),B(b)]-\mathbf {C} [A(a'),B(b')]\leq 2,$

where C denotes correlation.

Correlation of observables X, Y is defined as

$\mathbf {C} (X,Y)=\operatorname {E} (XY).$

This is a non-normalized form of the correlation coefficient considered in statistics (see Quantum correlation).

In order to formulate Bell's theorem, we formalize local realism as follows:

1. There is a probability space $\Lambda$ and the observed outcomes by both Alice and Bob result by random sampling of the parameter $\lambda \in \Lambda$.
2. The values observed by Alice or Bob are functions of the local detector settings and the hidden parameter only. Thus

• Value observed by Alice with detector setting a is $A(a,\lambda )$
• Value observed by Bob with detector setting b is $B(b,\lambda )$

Implicit in assumption 1) above, the hidden parameter space $\Lambda$ has a probability measure $\rho$ and the expectation of a random variable X on $\Lambda$ with respect to $\rho$ is written

$\operatorname {E} (X)=\int _{\Lambda }X(\lambda )\rho (\lambda )d\lambda$

where for accessibility of notation we assume that the probability measure has a density.

Bell's inequality. The CHSH inequality (1) holds under the hidden variables assumptions above.

For simplicity, let us first assume the observed values are +1 or −1; we remove this assumption in Remark 1 below.

Let $\lambda \in \Lambda$. Then at least one of

$B(b,\lambda )+B(b',\lambda ),\quad B(b,\lambda )-B(b',\lambda )$

is 0. Thus

$A(a,\lambda )\ B(b,\lambda )+A(a,\lambda )\ B(b',\lambda )+A(a',\lambda )\ B(b,\lambda )-A(a',\lambda )\ B(b',\lambda )=$

$=A(a,\lambda )(B(b,\lambda )+B(b',\lambda ))+A(a',\lambda )(B(b,\lambda )-B(b',\lambda ))\quad$

$\leq 2.$

and therefore

$\mathbf {C} (A(a),B(b))+\mathbf {C} (A(a),B(b'))+\mathbf {C} (A(a'),B(b))-\mathbf {C} (A(a'),B(b'))=$

$=\int _{\Lambda }A(a,\lambda )\ B(b,\lambda )\rho (\lambda )d\lambda +\int _{\Lambda }A(a,\lambda )\ B(b',\lambda )\rho (\lambda )d\lambda +\int _{\Lambda }A(a',\lambda )\ B(b,\lambda )\rho (\lambda )d\lambda -\int _{\Lambda }A(a',\lambda )\ B(b',\lambda )\rho (\lambda )d\lambda =$

$=\int _{\Lambda }{\bigg \{}A(a,\lambda )\ B(b,\lambda )+A(a,\lambda )\ B(b',\lambda )+A(a',\lambda )\ B(b,\lambda )-A(a',\lambda )\ B(b',\lambda ){\bigg \}}\rho (\lambda )d\lambda =$

$=\int _{\Lambda }{\bigg \{}A(a,\lambda )(B(b,\lambda )+B(b',\lambda ))+A(a',\lambda )(B(b,\lambda )-B(b',\lambda )){\bigg \}}\rho (\lambda )d\lambda \quad$

$\leq 2.$

Remark 1. The correlation inequality (1) still holds if the variables $A(a,\lambda )$, $B(b,\lambda )$ are allowed to take on any real values between −1 and +1. Indeed, the relevant idea is that each summand in the above average is bounded above by 2. This is easily seen to be true in the more general case:

$A(a,\lambda )\ B(b,\lambda )+A(a,\lambda )\ B(b',\lambda )+A(a',\lambda )\ B(b,\lambda )-A(a',\lambda )\ B(b',\lambda )=$

$=A(a,\lambda )(B(b,\lambda )+B(b',\lambda ))+A(a',\lambda )(B(b,\lambda )-B(b',\lambda ))\quad$

$\leq {\bigg |}A(a,\lambda )(B(b,\lambda )+B(b',\lambda ))+A(a',\lambda )(B(b,\lambda )-B(b',\lambda )){\bigg |}\quad$

$\leq {\bigg |}A(a,\lambda )(B(b,\lambda )+B(b',\lambda )){\bigg |}+{\bigg |}A(a',\lambda )(B(b,\lambda )-B(b',\lambda )){\bigg |}$

$\leq |B(b,\lambda )+B(b',\lambda )|+|B(b,\lambda )-B(b',\lambda )|\leq 2.$

To justify the upper bound 2 asserted in the last inequality, without loss of generality, we can assume that

$B(b,\lambda )\geq B(b',\lambda )\geq 0.$

In that case

$|B(b,\lambda )+B(b',\lambda )|+|B(b,\lambda )-B(b',\lambda )|=B(b,\lambda )+B(b',\lambda )+B(b,\lambda )-B(b',\lambda )=\quad$

$=2B(b,\lambda )\leq 2.\quad$

Remark 2. Though the important component of the hidden parameter $\lambda$ in Bell's original proof is associated with the source and is shared by Alice and Bob, there may be others that are associated with the separate detectors, these others being independent. This argument was used by Bell in 1971, and again by Clauser and Horne in 1974, to justify a generalisation of the theorem forced on them by the real experiments, in which detectors were never 100% efficient. The derivations were given in terms of the averages of the outcomes over the local detector variables. The formalisation of local realism was thus effectively changed, replacing A and B by averages and retaining the symbol $\lambda$ but with a slightly different meaning. It was henceforth restricted (in most theoretical work) to mean only those components that were associated with the source.

However, with the extension proved in Remark 1, CHSH inequality still holds even if the instruments themselves contain hidden variables. In that case, averaging over the instrument hidden variables gives new variables:

${\overline {A}}(a,\lambda ),\quad {\overline {B}}(b,\lambda )$

on $\Lambda$ which still have values in the range [−1, +1] to which we can apply the previous result.

Bell inequalities are violated by quantum mechanical predictions

In the usual quantum mechanical formalism, the observables X and Y are represented as self-adjoint operators on a Hilbert space. To compute the correlation, assume that X and Y are represented by matrices in a finite dimensional space and that X and Y commute; this special case suffices for our purposes below. The von Neumann measurement postulate states: a series of measurements of an observable X on a series of identical systems in state $\phi$ produces a distribution of real values. By the assumption that observables are finite matrices, this distribution is discrete. The probability of observing λ is non-zero if and only if λ is an eigenvalue of the matrix X and moreover the probability is

$\|\operatorname {E} _{X}(\lambda )\phi \|^{2}$

where E_X (λ) is the projector corresponding to the eigenvalue λ. The system state immediately after the measurement is

$\|\operatorname {E} _{X}(\lambda )\phi \|^{-1}\operatorname {E} _{X}(\lambda )\phi .$

From this, we can show that the correlation of commuting observables X and Y in a pure state $\psi$ is

$\langle XY\rangle =\langle XY\psi \mid \psi \rangle .$

We apply this fact in the context of the EPR paradox. The measurements performed by Alice and Bob are spin measurements on electrons. Alice can choose between two detector settings labelled a and a′; these settings correspond to measurement of spin along the z or the x axis. Bob can choose between two detector settings labelled b and b′; these correspond to measurement of spin along the z′ or x′ axis, where the x′ – z′ coordinate system is rotated 45° relative to the x – z coordinate system. The spin observables are represented by the 2 × 2 self-adjoint matrices:

$S_{x}={\begin{bmatrix}0&1\\1&0\end{bmatrix}},S_{z}={\begin{bmatrix}1&0\\0&-1\end{bmatrix}}.$

These are the Pauli spin matrices normalized so that the corresponding eigenvalues are +1, −1. As is customary, we denote the eigenvectors of S_x by

$\left|+x\right\rangle ,\quad \left|-x\right\rangle .$

Let $\phi$ be the spin singlet state for a pair of electrons discussed in the EPR paradox. This is a specially constructed state described by the following vector in the tensor product

$\left|\phi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|+x\right\rangle \otimes \left|-x\right\rangle -\left|-x\right\rangle \otimes \left|+x\right\rangle {\bigg )}.$

Now let us apply the CHSH formalism to the measurements that can be performed by Alice and Bob.

Illustration of Bell test for spin 1/2 particles. Source produces spin singlet pairs, one particle of each pair is sent to Alice and the other to Bob. Each performs one of the two spin measurements.

$A(a)=S_{z}\otimes I$

$A(a')=S_{x}\otimes I$

$B(b)=-{\frac {1}{\sqrt {2}}}\ I\otimes (S_{z}+S_{x})$

$B(b')={\frac {1}{\sqrt {2}}}\ I\otimes (S_{z}-S_{x}).$

The operators $B(b')$, $B(b)$ correspond to Bob's spin measurements along x′ and z′. Note that the A operators commute with the B operators, so we can apply our calculation for the correlation. In this case, we can show that the CHSH inequality fails. In fact, a straightforward calculation shows that

$\langle A(a)B(b)\rangle =\langle A(a')B(b)\rangle =\langle A(a')B(b')\rangle ={\frac {1}{\sqrt {2}}},$

and

$\langle A(a)B(b')\rangle =-{\frac {1}{\sqrt {2}}}.$

so that

$\langle A(a)B(b)\rangle +\langle A(a')B(b')\rangle +\langle A(a')B(b)\rangle -\langle A(a)B(b')\rangle ={\frac {4}{\sqrt {2}}}=2{\sqrt {2}}>2.$

Bell's Theorem: If the quantum mechanical formalism is correct, then the system consisting of a pair of entangled electrons cannot satisfy the principle of local realism. Note that $2{\sqrt {2}}$ is indeed the upper bound for quantum mechanics called Tsirelson's bound. The operators giving this maximal value are always isomorphic to the Pauli matrices.

Practical experiments testing Bell's theorem

Ver artigo principal: Bell test experiments

Scheme of a "two-channel" Bell test
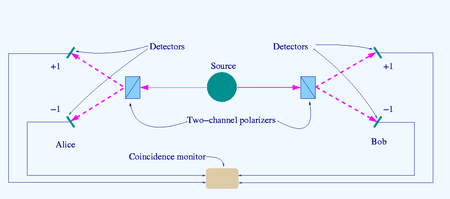
The source S produces pairs of "photons", sent in opposite directions. Each photon encounters a two-channel polariser whose orientation (a or b) can be set by the experimenter. Emerging signals from each channel are detected and coincidences of four types (++, −−, +− and −+) counted by the coincidence monitor.

Experimental tests can determine whether the Bell inequalities required by local realism hold up to the empirical evidence.

Bell's inequalities are tested by "coincidence counts" from a Bell test experiment such as the optical one shown in the diagram. Pairs of particles are emitted as a result of a quantum process, analysed with respect to some key property such as polarisation direction, then detected. The setting (orientations) of the analysers are selected by the experimenter.

Bell test experiments to date overwhelmingly violate Bell's inequality. Indeed, a table of Bell test experiments performed prior to 1986 is given in 4.5 of Redhead, 1987. Of the thirteen experiments listed, only two reached results contradictory to quantum mechanics; moreover, according to the same source, when the experiments were repeated, "the discrepancies with QM could not be reproduced".

Nevertheless, the issue is not conclusively settled. According to Shimony's 2004 Stanford Encyclopedia overview article:

Most of the dozens of experiments performed so far have favored Quantum Mechanics, but not decisively because of the 'detection loopholes' or the 'communication loophole.' The latter has been nearly decisively blocked by a recent experiment and there is a good prospect for blocking the former.

To explore the 'detection loophole', one must distinguish the classes of homogeneous and inhomogeneous Bell inequality.

The standard assumption in Quantum Optics is that "all photons of given frequency, direction and polarization are identical" so that photodetectors treat all incident photons on an equal basis. Such a fair sampling assumption generally goes unacknowledged, yet it effectively limits the range of local theories to those which conceive of the light field as corpuscular. The assumption excludes a large family of local realist theories, in particular, Max Planck's description. We must remember the cautionary words of Albert Einstein shortly before he died: "Nowadays every Tom, Dick and Harry ('jeder Kerl' in German original) thinks he knows what a photon is, but he is mistaken".

Objective physical properties for Bell’s analysis (local realist theories) include the wave amplitude of a light signal. Those who maintain the concept of duality, or simply of light being a wave, recognize the possibility or actuality that the emitted atomic light signals have a range of amplitudes and, furthermore, that the amplitudes are modified when the signal passes through analyzing devices such as polarizers and beam splitters. It follows that not all signals have the same detection probability.

Two classes of Bell inequalities

The fair sampling problem was faced openly in the 1970s. In early designs of their 1973 experiment, Freedman and Clauser used fair sampling in the form of the Clauser-Horne-Shimony-Holt (CHSH) hypothesis. However, shortly afterwards Clauser and Horne made the important distinction between inhomogeneous (IBI) and homogeneous (HBI) Bell inequalities. Testing an IBI requires that we compare certain coincidence rates in two separated detectors with the singles rates of the two detectors. Nobody needed to perform the experiment, because singles rates with all detectors in the 1970s were at least ten times all the coincidence rates. So, taking into account this low detector efficiency, the QM prediction actually satisfied the IBI. To arrive at an experimental design in which the QM prediction violates IBI we require detectors whose efficiency exceeds 82% for singlet states, but have very low dark rate and short dead and resolving times. This is well above the 30% achievable so Shimony’s optimism in the Stanford Encyclopedia, quoted in the preceding section, appears over-stated.

Practical challenges

Ver artigo principal: Loopholes in Bell test experiments

Because detectors don't detect a large fraction of all photons, Clauser and Horne recognized that testing Bell's inequality requires some extra assumptions. They introduced the No Enhancement Hypothesis (NEH):

a light signal, originating in an atomic cascade for example, has a certain probability of activating a detector. Then, if a polarizer is interposed between the cascade and the detector, the detection probability cannot increase.

Given this assumption, there is a Bell inequality between the coincidence rates with polarizers and coincidence rates without polarizers.

The experiment was performed by Freedman and Clauser, who found that the Bell's inequality was violated. So the no-enhancement hypothesis cannot be true in a local hidden variables model. The Freedman-Clauser experiment reveals that local hidden variables imply the new phenomenon of signal enhancement:

In the total set of signals from an atomic cascade there is a subset whose detection probability increases as a result of passing through a linear polarizer.

This is perhaps not surprising, as it is known that adding noise to data can, in the presence of a threshold, help reveal hidden signals (this property is known as stochastic resonance). One cannot conclude that this is the only local-realist alternative to Quantum Optics, but it does show that the word loophole is biased. Moreover, the analysis leads us to recognize that the Bell-inequality experiments, rather than showing a breakdown of realism or locality, are capable of revealing important new phenomena.

Theoretical challenges

Some advocates of the hidden variables idea believe that experiments have ruled out local hidden variables. They are ready to give up locality, explaining the violation of Bell's inequality by means of a "non-local" hidden variable theory, in which the particles exchange information about their states. This is the basis of the Bohm interpretation of quantum mechanics, which requires that all particles in the universe be able to instantaneously exchange information with all others. A recent experiment ruled out a large class of non-Bohmian "non-local" hidden variable theories.

If the hidden variables can communicate with each other faster than light, Bell's inequality can easily be violated. Once one particle is measured, it can communicate the necessary correlations to the other particle. Since in relativity the notion of simultaneity is not absolute, this is unattractive. One idea is to replace instantaneous communication with a process which travels backwards in time along the past Light cone. This is the idea behind a transactional interpretation of quantum mechanics, which interprets the statistical emergence of a quantum history as a gradual coming to agreement between histories that go both forward and backward in time.

Recent controversial work by Joy Christian claims that a deterministic, local, and realistic theory can violate Bell's inequalities if the observables are chosen to be non-commuting numbers rather than commuting numbers as Bell had assumed. Christian claims that in this way the statistical predictions of quantum mechanics can be exactly reproduced. The controversy around his work concerns his noncommutative averaging procedure, in which the averages of products of variables at distant sites depend on the order in which they appear in an averaging integral. To many, this looks like nonlocal correlations, although Christian defines locality so that this type of thing is allowed. In his work, Christian builds up a CM view of the Bell's experiment that respects the rotational entanglement of physical reality, which is included in the QM view by construction, as this property of reality manifests itself clearly in the spin of particles, but it is not usually taken into account in the classical realm. Upon building this classical view, Christian suggests that in essence, it is this property of reality that results in the increased values of Bell's inequalities and as a result a local, realistic theory can be constructed. Moreover, Christian suggests a completely macro-object experiment, consisting of thousands of metal spheres, could recreate the results of the usual experiments.

The quantum mechanical wavefunction can also provide a local realistic description, if the wavefunction values are interpreted as the fundamental quantities that describe reality. Such an approach is called a many-worlds interpretation of quantum mechanics. In this controversial view, two distant observers both split into superpositions when measuring a spin. The Bell inequality violations are no longer counterintuitive, because it is not clear which copy of the observer B observer A will see when going to compare notes. If reality includes all the different outcomes, locality in physical space (not outcome space) places no restrictions on how the split observers can meet up.

This implies that there is a subtle assumption in the argument that realism is incompatible with quantum mechanics and locality. The assumption, in its weakest form, is called counterfactual definiteness. This states that if the result of an experiment are always observed to be definite, there is a quantity which determines what the outcome would have been even if you don't do the experiment.

Many worlds interpretations are not only counterfactually indefinite, they are factually indefinite. The results of all experiments, even ones that have been performed, are not uniquely determined.

Final remarks

The phenomenon of quantum entanglement that is behind violation of Bell's inequality is just one element of quantum physics which cannot be represented by any classical picture of physics; other non-classical elements are complementarity and wavefunction collapse. The problem of interpretation of quantum mechanics is intended to provide a satisfactory picture of these non-classical elements of quantum physics.

The EPR paper "pinpointed" the unusual properties of the entangled states, e.g. the above-mentioned singlet state, which is the foundation for present-day applications of quantum physics, such as quantum cryptography. This strange non-locality was originally supposed to be a Reductio ad absurdum, because the standard interpretation could easily do away with action-at-a-distance by simply assigning to each particle definite spin-states. Bell's theorem showed that the "entangledness" prediction of quantum mechanics have a degree of non-locality that cannot be explained away by any local theory.

In well-defined Bell experiments (see the paragraph on "test experiments") one can now falsify either quantum mechanics or Einstein's quasi-classical assumptions : presently many experiments of this kind have been performed, and the experimental results support quantum mechanics, though some believe that detectors give a biased sample of photons, so that until nearly every photon pair generated is observed there will be loopholes.

What is powerful about Bell's theorem is that it doesn't come from any particular physical theory. What makes Bell's theorem unique and powerful is that it relies only on the general properties of quantum mechanics. No physical theory which assumes a deterministic variable inside the particle that determines the outcome, can account for the experimental results, only assuming that this variable cannot acausally change other variables far away.

See also

• Bell test experiments
• CHSH Bell test
• Clauser and Horne's 1974 Bell test
• Counterfactual definiteness
• Leggett–Garg inequality
• Local hidden variable theory
• Mott problem
• Quantum entanglement
• Quantum mechanical Bell test prediction
• Measurement in quantum mechanics
• Renninger negative-result experiment
• GHZ State

References

• A. Aspect et al., Experimental Tests of Realistic Local Theories via Bell's Theorem, Phys. Rev. Lett. 47, 460 (1981)
• A. Aspect et al., Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell's Inequalities, Phys. Rev. Lett. 49, 91 (1982).
• A. Aspect et al., Experimental Test of Bell's Inequalities Using Time-Varying Analyzers, Phys. Rev. Lett. 49, 1804 (1982).
• A. Aspect and P. Grangier, About resonant scattering and other hypothetical effects in the Orsay atomic-cascade experiment tests of Bell inequalities: a discussion and some new experimental data, Lettere al Nuovo Cimento 43, 345 (1985)
• B. D'Espagnat, The Quantum Theory and Reality, Scientific American, 241, 158 (1979)
• J. S. Bell, On the problem of hidden variables in quantum mechanics, Rev. Mod. Phys. 38, 447 (1966)
• J. S. Bell, Introduction to the hidden variable question, Proceedings of the International School of Physics 'Enrico Fermi', Course IL, Foundations of Quantum Mechanics (1971) 171–81
• J. S. Bell, Bertlmann’s socks and the nature of reality, Journal de Physique, Colloque C2, suppl. au numero 3, Tome 42 (1981) pp C2 41–61
• J. S. Bell, Speakable and Unspeakable in Quantum Mechanics (Cambridge University Press 1987) [A collection of Bell's papers, including all of the above.]
• J. F. Clauser and A. Shimony, Bell's theorem: experimental tests and implications, Reports on Progress in Physics 41, 1881 (1978)
• J. F. Clauser and M. A. Horne, Phys. Rev D 10, 526–535 (1974)
• E. S. Fry, T. Walther and S. Li, Proposal for a loophole-free test of the Bell inequalities, Phys. Rev. A 52, 4381 (1995)
• E. S. Fry, and T. Walther, Atom based tests of the Bell Inequalities — the legacy of John Bell continues, pp 103–117 of Quantum [Un]speakables, R.A. Bertlmann and A. Zeilinger (eds.) (Springer, Berlin-Heidelberg-New York, 2002)
• R. B. Griffiths, Consistent Quantum Theory', Cambridge University Press (2002).
• L. Hardy, Nonlocality for 2 particles without inequalities for almost all entangled states. Physical Review Letters 71 (11) 1665–1668 (1993)
• M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press (2000)
• P. Pearle, Hidden-Variable Example Based upon Data Rejection, Physical Review D 2, 1418–25 (1970)
• A. Peres, Quantum Theory: Concepts and Methods, Kluwer, Dordrecht, 1993.
• P. Pluch, Theory of Quantum Probability, PhD Thesis, University of Klagenfurt, 2006.
• B. C. van Frassen, Quantum Mechanics, Clarendon Press, 1991.
• M.A. Rowe, D. Kielpinski, V. Meyer, C.A. Sackett, W.M. Itano, C. Monroe, and D.J. Wineland, Experimental violation of Bell's inequalities with efficient detection,(Nature, 409, 791–794, 2001).
• S. Sulcs, The Nature of Light and Twentieth Century Experimental Physics, Foundations of Science 8, 365–391 (2003)
• S. Gröblacher et al., An experimental test of non-local realism,(Nature, 446, 871–875, 2007).
• D. N. Matsukevich, P. Maunz, D. L. Moehring, S. Olmschenk, and C. Monroe, Bell Inequality Violation with Two Remote Atomic Qubits, Phys. Rev. Lett. 100, 150404 (2008).

Further reading

The following are intended for general audiences.

• Amir D. Aczel, Entanglement: The greatest mystery in physics (Four Walls Eight Windows, New York, 2001).
• A. Afriat and F. Selleri, The Einstein, Podolsky and Rosen Paradox (Plenum Press, New York and London, 1999)
• J. Baggott, The Meaning of Quantum Theory (Oxford University Press, 1992)
• N. David Mermin, "Is the moon there when nobody looks? Reality and the quantum theory", in Physics Today, April 1985, pp. 38–47.
• Louisa Gilder, The Age of Entanglement: When Quantum Physics Was Reborn (New York: Alfred A. Knopf, 2008)
• Brian Greene, The Fabric of the Cosmos (Vintage, 2004, ISBN 0-375-72720-5)
• Nick Herbert, Quantum Reality: Beyond the New Physics (Anchor, 1987, ISBN 0-385-23569-0)
• D. Wick, The infamous boundary: seven decades of controversy in quantum physics (Birkhauser, Boston 1995)
• R. Anton Wilson, Prometheus Rising (New Falcon Publications, 1997, ISBN 1-56184-056-4)
• Gary Zukav "The Dancing Wu Li Masters" (Perennial Classics, 2001, ISBN 0-06-095968-1)

External links

• An explanation of Bell's Theorem, based on N. D. Mermin's article, "Bringing Home the Atomic World: Quantum Mysteries for Anybody," Am. J. of Phys. 49 (10), 940 (October 1981)
• Quantum Entanglement Includes a simple explanation of Bell's Inequality.
• Bell's theorem on arXiv.org
• Disproofs of Bell, GHZ, and Hardy Type Theorems and the Illusion of Entanglement Disproof of Bell's Theorem

Category:Fundamental physics concepts Category:Quantum information science Category:Quantum measurement Category:Physics theorems Category:Quantum mechanics Category:Hidden variable theory Category:Articles with Alice and Bob explanations Category:Inequalities pt:Teorema de Bell

Predefinição:Quantum mechanics The Bell test experiments serve to investigate the validity of the entanglement effect in quantum mechanics by using some kind of Bell inequality. John Bell published the first inequality of this kind in his paper "On the Einstein-Podolsky-Rosen Paradox". Bell's Theorem states that a Bell inequality must be obeyed under any local hidden variable theory but can in certain circumstances be violated under quantum mechanics. The term "Bell inequality" can mean any one of a number of inequalities — in practice, in real experiments, the CHSH or CH74 inequality, not the original one derived by John Bell. It places restrictions on the statistical results of experiments on sets of particles that have taken part in an interaction and then separated. A Bell test experiment is one designed to test whether or not the real world obeys a Bell inequality. Such experiments fall into two classes, depending on whether the analysers used have one or two output channels.

Conduct of optical Bell test experiments

In practice most actual experiments have used light, assumed to be emitted in the form of particle-like photons (produced by atomic cascade or spontaneous parametric down conversion), rather than the atoms that Bell originally had in mind. The property of interest is, in the best known experiments, the polarisation direction, though other properties can be used.

A typical CHSH (two-channel) experiment

Scheme of a "two-channel" Bell test
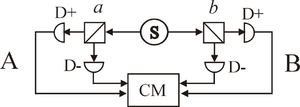
The source S produces pairs of "photons", sent in opposite directions. Each photon encounters a two-channel polariser whose orientation can be set by the experimenter. Emerging signals from each channel are detected and coincidences counted by the coincidence monitor CM.

The diagram shows a typical optical experiment of the two-channel kind for which Alain Aspect set a precedent in 1982 (Aspect, 1982a). Coincidences (simultaneous detections) are recorded, the results being categorised as '++', '+−', '−+' or '−−' and corresponding counts accumulated.

Four separate subexperiments are conducted, corresponding to the four terms E(a, b) in the test statistic S ((2) below). The settings a, a′, b and b′ are generally in practice chosen to be 0, 45°, 22.5° and 67.5° respectively — the "Bell test angles" — these being the ones for which the quantum mechanical formula gives the greatest violation of the inequality.

For each selected value of a and b, the numbers of coincidences in each category (N₊₊, N_--, N_+- and N_-+) are recorded. The experimental estimate for E(a, b) is then calculated as:

(1)        E = (N₊₊ + N_-- − N_+- − N_-+)/(N₊₊ + N_-- + N_+- + N_-+).

Once all four E’s have been estimated, an experimental estimate of the test statistic

(2)       S = E(a, b) − E(a, b′) + E(a′, b) + E(a′ b′)

can be found. If S is numerically greater than 2 it has infringed the CHSH inequality. The experiment is declared to have supported the QM prediction and ruled out all local hidden variable theories.

A strong assumption has had to be made, however, to justify use of expression (2). It has been assumed that the sample of detected pairs is representative of the pairs emitted by the source. That this assumption may not be true comprises the fair sampling loophole.

The derivation of the inequality is given in the CHSH Bell test page.

A typical CH74 (single-channel) experiment

Ficheiro:Single-channel Bell test.png

Setup for a "single-channel" Bell test
The source S produces pairs of "photons", sent in opposite directions. Each photon encounters a single channel (e.g. "pile of plates") polariser whose orientation can be set by the experimenter. Emerging signals are detected and coincidences counted by the coincidence monitor CM.

Prior to 1982 all actual Bell tests used "single-channel" polarisers and variations on an inequality designed for this setup. The latter is described in Clauser, Horne, Shimony and Holt's much-cited 1969 article (Clauser, 1969) as being the one suitable for practical use. As with the CHSH test, there are four subexperiments in which each polariser takes one of two possible settings, but in addition there are other subexperiments in which one or other polariser or both are absent. Counts are taken as before and used to estimate the test statistic.

(3)       S = (N(a, b) − N(a, b′) + N(a′, b) + N(a′, b′) − N(a′, ∞) − N(∞, b)) / N(∞, ∞),

where the symbol ∞ indicates absence of a polariser.

If S exceeds 0 then the experiment is declared to have infringed Bell's inequality and hence to have "refuted local realism".

The only theoretical assumption (other than Bell's basic ones of the existence of local hidden variables) that has been made in deriving (3) is that when a polariser is inserted the probability of detection of any given photon is never increased: there is "no enhancement". The derivation of this inequality is given in the page on Clauser and Horne's 1974 Bell test.

Experimental assumptions

In addition to the theoretical assumptions made, there are practical ones. There may, for example, be a number of "accidental coincidences" in addition to those of interest. It is assumed that no bias is introduced by subtracting their estimated number before calculating S, but that this is true is not considered by some to be obvious. There may be synchronisation problems — ambiguity in recognising pairs due to the fact that in practice they will not be detected at exactly the same time.

Nevertheless, despite all these deficiencies of the actual experiments, one striking fact emerges: the results are, to a very good approximation, what quantum mechanics predicts. If imperfect experiments give us such excellent overlap with quantum predictions, most working quantum physicists would agree with John Bell in expecting that, when a perfect Bell test is done, the Bell inequalities will still be violated. This attitude has led to the emergence of a new sub-field of physics which is now known as quantum information theory. One of the main achievements of this new branch of physics is showing that violation of Bell's inequalities leads to the possibility of a secure information transfer, which utilizes the so-called quantum cryptography (involving entangled states of pairs of particles).

Notable experiments

Over the past thirty or so years, a great number of Bell test experiments have now been conducted. These experiments have (subject to a few assumptions, considered by most to be reasonable) confirmed quantum theory and shown results that cannot be explained under local hidden variable theories. Advancements in technology have led to significant improvement in efficiencies, as well as a greater variety of methods to test the Bell Theorem.

Some of the best known:

Freedman and Clauser, 1972

This was the first actual Bell test, using Freedman's inequality, a variant on the CH74 inequality.

Aspect, 1981-2

Aspect and his team at Orsay, Paris, conducted three Bell tests using calcium cascade sources. The first and last used the CH74 inequality. The second was the first application of the CHSH inequality, the third the famous one (originally suggested by John Bell) in which the choice between the two settings on each side was made during the flight of the photons.

Tittel and the Geneva group, 1998

The Geneva 1998 Bell test experiments showed that distance did not destroy the "entanglement". Light was sent in fibre optic cables over distances of several kilometers before it was analysed. As with almost all Bell tests since about 1985, a "parametric down-conversion" (PDC) source was used.

Weihs' experiment under "strict Einstein locality" conditions

In 1998 Gregor Weihs and a team at Innsbruck, lead by Anton Zeilinger, conducted an ingenious experiment that closed the "locality" loophole, improving on Aspect's of 1982. The choice of detector was made using a quantum process to ensure that it was random. This test violated the CHSH inequality by over 30 standard deviations, the coincidence curves agreeing with those predicted by quantum theory.

Pan et al.'s experiment on the GHZ state

This is the first of new Bell-type experiments on more than two particles; this one uses the so-called GHZ state of three particles; it is reported in Nature (2000)

Gröblacher et al. (2007) test of Leggett-type non-local realist theories

The authors interpret their results as disfavouring "realism" and hence allow QM to be local but "non-real". However they have actually only ruled out a specific class of non-local theories suggested by Anthony Leggett.

Salart et al. (2008) Separation in a Bell Test

This experiment filled a loophole by providing an 18 km separation between detectors, which is sufficient to allow the completion of the quantum state measurements before any information could have traveled between the two detectors. The test confirmed the non-local nature of quantum correlations.

Loopholes

Ver artigo principal: Loopholes in Bell test experiments

Though the series of increasingly sophisticated Bell test experiments has convinced the physics community in general that local realism is untenable, there are still critics who point out that the outcome of every single experiment done so far that violates a Bell inequality can, at least theoretically, be explained by faults in the experimental setup, experimental procedure or that the equipment used do not behave as well as it is supposed to. These possibilities are known as "loopholes". The most serious loophole is the detection loophole, which means that particles are not always detected in both wings of the experiment. It is possible to "engineer" quantum correlations (the experimental result) by letting detection be dependent on a combination of local hidden variables and detector setting. Experimenters have repeatedly stated that loophole-free tests can be expected in the near future (García-Patrón, 2004). On the other hand, some researchers point out that it is a logical possibility that quantum physics itself prevents a loophole-free test from ever being implemented (Gill, 2003; Santos, 2006).

References

• Aspect, 1981: A. Aspect et al., Experimental Tests of Realistic Local Theories via Bell's Theorem, Phys. Rev. Lett. 47, 460 (1981)
• Aspect, 1982a: A. Aspect et al., Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell's Inequalities, Phys. Rev. Lett. 49, 91 (1982),
• Aspect, 1982b: A. Aspect et al., Experimental Test of Bell's Inequalities Using Time-Varying Analyzers, Phys. Rev. Lett. 49, 1804 (1982),
• Barrett, 2002 Quantum Nonlocality, Bell Inequalities and the Memory Loophole: quant-ph/0205016 (2002).
• Bell, 1987: J. S. Bell, Speakable and Unspeakable in Quantum Mechanics, (Cambridge University Press 1987)
• Clauser, 1969: J. F. Clauser, M.A. Horne, A. Shimony and R. A. Holt, Proposed experiment to test local hidden-variable theories, Phys. Rev. Lett. 23, 880-884 (1969),
• Clauser, 1974: J. F. Clauser and M. A. Horne, Experimental consequences of objective local theories, Phys. Rev. D 10, 526-35 (1974)
• Freedman, 1972: S. J. Freedman and J. F. Clauser, Experimental test of local hidden-variable theories, Phys. Rev. Lett. 28, 938 (1972)
• García-Patrón, 2004: R. García-Patrón, J. Fiurácek, N. J. Cerf, J. Wenger, R. Tualle-Brouri, and Ph. Grangier, Proposal for a Loophole-Free Bell Test Using Homodyne Detection, Phys. Rev. Lett. 93, 130409 (2004)
• Gill, 2003: R.D. Gill, Time, Finite Statistics, and Bell's Fifth Position: quant-ph/0301059, Foundations of Probability and Physics - 2, Vaxjo Univ. Press, 2003, 179-206 (2003)
• Kielpinski: D. Kielpinski et al., Recent Results in Trapped-Ion Quantum Computing (2001)
• Kwiat, 1999: P.G. Kwiat, et al., Ultrabright source of polarization-entangled photons, Physical Review A 60 (2), R773-R776 (1999)
• Rowe, 2001: M. Rowe et al., Experimental violation of a Bell’s inequality with efficient detection, Nature 409, 791 (2001)
• Santos, 2005: E. Santos, Bell's theorem and the experiments: Increasing empirical support to local realism: quant-ph/0410193, Studies In History and Philosophy of Modern Physics, 36, 544-565 (2005)
• Tittel, 1997: W. Tittel et al., Experimental demonstration of quantum-correlations over more than 10 kilometers, Phys. Rev. A, 57, 3229 (1997)
• Tittel, 1998: W. Tittel et al., Experimental demonstration of quantum-correlations over more than 10 kilometers, Physical Review A 57, 3229 (1998); Violation of Bell inequalities by photons more than 10 km apart, Physical Review Letters 81, 3563 (1998)
• Weihs, 1998: G. Weihs, et al., Violation of Bell’s inequality under strict Einstein locality conditions, Phys. Rev. Lett. 81, 5039 (1998)

In Bell test experiments, there may be experimental problems that affect the validity of the experimental findings. The term "Loopholes" is frequently used to denote these problems. See the page on Bell's theorem for the theoretical background to these experimental efforts (see also J. S. Bell 1928-1990). The purpose of the experiment is to test whether nature is best described using a Local hidden variable theory or by the quantum entanglement hypothesis of Quantum mechanics.

The "fair sampling" or "efficiency" problem is the most prominent problem, and affects all experiments performed to date save one (Rowe et al., 2001). This problem was noted first by Pearle in 1970, and Clauser and Horne (1974) devised another result intended to take care of this. Some results were also obtained in the 1980s but the subject has undergone significant research in recent years. The many experiments affected by this problem deal with it without exception by using the "fair sampling" assumption. More on this below.

In some experiments there also may be other possibilities that make "local realist" explanations of Bell test violations possible, these are briefly described below. Each needs to be checked for and screened out before an experiment can be said to rule out local realism, and at least in modern setups, the experimenters do their best to reduce these problems to a minimum.

Many modern experiments are directed at detecting quantum entanglement rather than ruling out Local hidden variable theories, and that task is different since one accepts quantum mechanics at the outset (no entanglement without Quantum mechanics). This is regularly done using Bell's theorem, but in this situation the theorem is used as an Entanglement witness, a dividing line between entangled quantum states and separable quantum states and is then, as such, not as sensitive to the problems described here.

Sources of error in (optical) Bell test experiments

In the case of Bell test experiments, if there are sources of error (that are not accounted for by the experimentalists) that might be of enough importance to explain why a particular experiment gives results in favor of quantum entanglement as opposed to local realism, they are called "loopholes." Here some examples of existing and hypothetical experimental errors are explained. There are of course sources of error in all physical experiments. Whether or not any of those presented here have been found important enough to be called loopholes, in general or because of possible mistakes by the performers of some known experiment found in literature, is discussed in the subsequent sections. There are also non-optical Bell test experiments, which are not discussed here.

Example of typical experiment

Scheme of a CHSH "two-channel" optical Bell test
The source S is assumed to produce pairs of "photons," one pair at a time with the individual photons sent in opposite directions. Each photon encounters a two-channel polarizer whose orientation can be set by the experimenter. Emerging signals from each channel are detected and coincidences counted by the "coincidence monitor" CM. It is assumed that any individual photon has to go one way or the other at the polarizer. The entanglement hypothesis states that the two photons in a pair (due to their common origin) "share a wave function" and that a measurement on one of the photons affects the other instantaneously no matter the separation between them, a fact pointed out in the EPR paradox. The Local realism hypothesis on the other hand states that measurement on one photon has no influence whatsoever on the other.

As a basis for our description of experimental errors let us consider a typical experiment of CHSH type (see picture to the right). In the experiment the source is assumed to emit light in the form of pairs of particle-like photons with each photon sent off in opposite directions. When photons are detected simultaneously (in reality during the same short time interval) at both sides of the "coincidence monitor" a coincident detection is counted. On each side of the "coincidence monitor" there are two inputs that are here named the "+" and the "-" input. The individual photons must (according to quantum mechanics) make a choice and go one way or the other at a two-channel polarizer. For each pair emitted at the source ideally either the "+" or the "-" input on both sides will detect a photon. The four possibilities can be categorized as '++', '+−', '−+' and '−−' and the number of simultaneous detections of all four types (N++, N+-, N-+, N--) is counted over a timespan covering a number of emissions from the source. Then the following is calculated:

(1) E = (N++ + N-- − N+- − N-+)/(N++ + N-- + N+- + N-+).

This is done with polarizer a rotated into two positions that we could call "a" and "a'" and polarizer b into two positions that we could call "b" and "b'" so we get E(a,b),E(a,b'),E(a',b) and E(a',b'). Then the following is calculated:

(2) S = E(a, b) − E(a, b′) + E(a′, b) + E(a′ b′)

Entanglement and local realism give different predicted values on S, thus the experiment (if there are no substantial sources of error) gives an indication to which of the two theories better correspond to reality.

Sources of error in the light source

The principal possible errors in the light source are:

• Failure of rotational invariance: The light from the source might have a preferred polarization direction, in which case it is not rotationally invariant.
• Multiple emissions: The light source might emit several pairs at the same time or within a short timespan causing error at detection.

Sources of error in the optical polarizer

• Imperfections in the polarizer: The polarizer might influence the relative amplitude or other aspects of reflected and transmitted light in various ways.

Sources of error in the detector or detector settings

• The experiment may be set up as not being able to detect photons simultaneously in the "+" and "-" input on the same side of the experiment. If the source may emit more than one pair of photons at any one instant in time or close in time after one another, for example, this could cause errors in the detection.
• Imperfections in the detector: failing to detect some photons or detecting photons even when the light source is turned off (noise).

Detection efficiency loophole and the fair sampling assumption

In Bell test experiments one problem is that detection efficiency may be less than 100%, and this is always the case in optical experiments. This changes the inequalities to be used, for example the CHSH inequality:

$-2\leq E(a,b)-E(a,b')+E(a',b)+E(a',b')\leq 2$

When data from an experiment is used in the inequality one needs to condition on that a "coincidence" occurred, that a detection occurred in both wings of the experiment. This will change the inequality into

${\big |}E(AC'|{\text{coinc.}})+E(AD'|{\text{coinc.}}){\big |}+{\big |}E(BC'|{\text{coinc.}})-E(BD'|{\text{coinc.}}){\big |}\leq {\frac {4}{\eta }}-2$

In this formula, the $\eta$ denotes the efficiency of the experiment, formally the minimum probability of a coincidence given a detection on one side (Garg & Mermin, 1987; Larsson 1998). In Quantum mechanics, the left-hand side reaches $2{\sqrt {2}}$, which is greater than two, but for a non-100% efficiency the latter formula has a larger right-hand side. And at low efficiency (below $2({\sqrt {2}}-1)$≈82%), the inequality is no longer violated.

Usually, the "fair sampling assumption" is used in this situation (alternatively, the "no-enhancement assumption"). It states that the sample of detected pairs is representative of the pairs emitted, in which case the right-hand side above is reduced to 2, irrespective of the efficiency. Please note that this comprises a third postulate necessary for violation in low-efficiency experiments, in addition to the (two) postulates of Local Realism. There is unfortunately no way to test experimentally whether a given experiment does fair sampling, so it is really an assumption if a very natural one.

There are tests that are not sensitive to this problem, such as the Clauser-Horne test, but these have the same performance as the latter of the two inequalities above; they cannot be violated unless the efficiency exceeds a certain bound. For example, in the Clauser-Horne test, the bound is ⅔≈67% (Eberhard, 199X; Larsson, 2000).

With only one exception, all Bell test experiments to date are affected by this problem, and a typical optical experiment has around 5-30% efficiency. The bounds are actively pursued at the moment (2006). The exception to the rule, the Rowe et al. (2001) experiment is performed using two ions rather than photons, and had 100% efficiency. Unfortunately, it has its own problems, see below.{{carece de fontes}}

Other loopholes

Failure of rotational invariance

The source is said to be "rotationally invariant" if all possible hidden variable values (describing the states of the emitted pairs) are equally likely. The general form of a Bell test does not assume rotational invariance, but a number of experiments have been analysed using a simplified formula that depends upon it. It is possible that there has not always been adequate testing to justify this. Even where, as is usually the case, the actual test applied is general, if the hidden variables are not rotationally invariant this can result in misleading descriptions of the results. Graphs may be presented, for example, of coincidence rate against the difference between the settings a and b, but if a more comprehensive set of experiments had been done it might have become clear that the rate depended on a and b separately. Cases in point may be Weihs’ experiment (Weihs, 1998), presented as having closed the “locality” loophole, and Kwiat’s demonstration of entanglement using an “ultrabright photon source” (Kwiat, 1999).

Double detections

In many experiments the electronics is such that simultaneous ‘+’ and ‘–’ counts from both outputs of a polariser can never occur, only one or the other being recorded. Under quantum mechanics, they will not occur anyway, but under a wave theory the suppression of these counts will cause even the basic realist prediction to yield “unfair sampling”. The effect is negligible, however, if the detection efficiencies are low.

Locality

Another problem is the so-called “locality” or “light-cone” loophole. The Bell inequality is motivated by the absence of communication between the two measurement sites. In experiments, this is usually ensured simply by prohibiting any light-speed communication by separating the two sites and then ensuring that the measurement duration is shorter than the time it would take for any light-speed signal from one site to the other, or indeed, to the source. An experiment that does not do this cannot test Local Realism, for obvious reasons. Note that the needed mechanism would necessarily be outside Quantum Mechanics, and needs to explain “entanglement” in a great variety of geometrical setups, over distances of several kilometers, and between a variety of systems.

There are, so far, not so many experiments that really rule out the locality loophole. John Bell supported Aspect’s investigation of it (Bell, 1987b, p. 109) and had some active involvement with the work, being on the examining board for Aspect’s PhD. Aspect improved the separation of the sites and did the first attempt on really having independent random detector orientations. Weihs et al. improved on this with a distance on the order of a few hundred meters in their experiment in addition to using random settings retrieved from a quantum system. This remains the best attempt to date.

This loophole is more hypothetical than the other possible loopholes in that there are no known physical mechanisms that could cause a problem due to locality.

Superdeterminism

Even if all experimental loopholes are closed, there is still a theoretical loophole that may allow the construction of a local realist theory that agrees with experiment. Bell's Theorem assumes that the polarizer settings can be chosen independently of any local hidden variable that determines the detection probabilities. But if both the polarizer settings and the experimental outcome are determined by a variable in their common past, the observed detection rates could be produced without information travelling faster than light (Bell, 1987a). Bell has referred to this possibility as "superdeterminism" (Bell, 1985).

References

• Bell, 1985: J. S. Bell, BBC Radio interview with Paul Davies, 1985
• Bell, 1987a: J. S. Bell, Free variables and local causality, Epistemological Letters, Feb. 1977. Reprinted as Chapter 12 of J. S. Bell, Speakable and Unspeakable in Quantum Mechanics, (Cambridge University Press 1987)
• Bell, 1987b: J. S. Bell, Atomic-cascade photons and quantum-mechanical nonlocality. Reprinted as Chapter 13 of J. S. Bell, Speakable and Unspeakable in Quantum Mechanics, (Cambridge University Press 1987)
• Clauser, 1974: J. F. Clauser and M. A. Horne, Experimental consequences of objective local theories, Phys. Rev. D 10, 526-35 (1974)
• Freedman, 1972: S. J. Freedman and J. F. Clauser, Phys. Rev. Lett. 28, 938 (1972)
• Garg and Mermin: A. Garg and N.D. Mermin, Detector inefficiencies in the Einstein-Podolsky-Rosen experiment Phys. Rev. D 35, 3831 - 3835 (1987)
• Kwiat, 1999: P.G. Kwiat, et al., Ultrabright source of polarization-entangled photons, Physical Review A 60 (2), R773-R776 (1999)
• Larsson, J-A. Larsson, Bell’s inequality and detector inefficiency Phys. Rev. A 57, 3304 - 3308 (1998)
• P Pearle, Hidden-Variable Example Based upon Data Rejection, Phys. Rev. D, 2, 1418-25 (1970)
• Thompson, 1996: C. H. Thompson, The Chaotic Ball: An Intuitive Analogy for EPR Experiments, Found. Phys. Lett. 9, 357 (1996)
• Tittel, 1997: W. Tittel et al., Experimental demonstration of quantum-correlations over more than 10 kilometers, Phys. Rev. A, 57, 3229 (1997)
• Tittel, 1999: W. Tittel et al., Long-distance Bell-type tests using energy-time entangled photons, Phys. Rev. A, 59, 4150 (1999)
• Weihs, 1998: G. Weihs, et al., Violation of Bell’s inequality under strict Einstein locality conditions, Phys. Rev. Lett. 81, 5039 (1998)

The measurement problem in quantum mechanics is the unresolved problem of how (or if) wavefunction collapse occurs. The inability to observe this process directly has given rise to different interpretations of quantum mechanics, and poses a key set of questions that each interpretation must answer. The wavefunction in quantum mechanics evolves according to the Schrödinger equation into a linear superposition of different states, but actual measurements always find the physical system in a definite state. Any future evolution is based on the state the system was discovered to be in when the measurement was made, meaning that the measurement "did something" to the process under examination. Whatever that "something" may be does not appear to be explained by the basic theory.

To express matters differently (to paraphrase Steven Weinberg ), the wave function evolves deterministically – knowing the wave function at one moment, the Schrödinger equation determines the wave function at any later time. If observers and their measuring apparatus are themselves described by a deterministic wave function, why can we not predict precise results for measurements, but only probabilities? As a general question: How can one establish a correspondence between quantum and classical reality?

Example

The best known example is the "paradox" of the Schrödinger's cat: a cat is apparently evolving into a linear superposition of basis vectors that can be characterized as an "alive cat" and states that can be described as a "dead cat". Each of these possibilities is associated with a specific nonzero probability amplitude; the cat seems to be in a "mixed" state. However, a single, particular observation of the cat does not measure the probabilities: it always finds either a living cat, or a dead cat. After the measurement the cat is definitively alive or dead. The question is: How are the probabilities converted into an actual, sharply well-defined outcome?

Interpretations

Ver artigo principal: Interpretations of quantum mechanics

Some interpretations claim that the latter approach was put on firm ground in the 1980s by the phenomenon of quantum decoherence. It is claimed that decoherence makes it possible to identify the fuzzy boundary between the quantum microworld and the world where the classical intuition is applicable. Quantum decoherence was proposed in the context of the many-worlds interpretation{{carece de fontes}}, but it has also become an important part of some modern updates of the Copenhagen interpretation based on consistent histories ("Copenhagen done right").{{carece de fontes}} Quantum decoherence does not describe the actual process of the wavefunction collapse, but it explains the conversion of the quantum probabilities (that are able to interfere) to the ordinary classical probabilities. See, for example, Zurek, Zeh and Schlosshauer.

Hugh Everett's relative state interpretation, also referred to as the many-worlds interpretation, attempts to avoid the problem by suggesting it is an illusion. Under this system there is only one wavefunction, the superposition of the entire universe, and it never collapses -- so there is no measurement problem. Instead the act of measurement is actually an interaction between two quantum entities, which entangle to form a single larger entity, for instance living cat/happy scientist. Everett also attempted to demonstrate the way that in measurements the probabilistic nature of quantum mechanics would appear; work later extended by Bryce DeWitt and others and renamed the many-worlds interpretation. Everett/DeWitt's interpretation posits a single universal wavefunction, but with the added proviso that "reality" from the point of view of any single observer, "you", is defined as a single path in time through the superpositions. That is, "you" have a history that is made of the outcomes of measurements you made in the past, but there are many other "yous" with slight variations in history. Under this system our reality is one of many similar ones.

The Bohm interpretation tries to solve the measurement problem very differently: this interpretation contains not only the wavefunction, but also the information about the position of the particle(s). The role of the wavefunction is to create a "quantum potential" that influences the motion of the "real" particle in such a way that the probability distribution for the particle remains consistent with the predictions of the orthodox quantum mechanics. According to the Bohm interpretation combined with the von Neumann theory of measurement in quantum mechanics, once the particle is observed, other wave-function channels remain empty and thus ineffective, but there is no true wavefunction collapse. Decoherence provides that this ineffectiveness is stable and irreversible, which explains the apparent wavefunction collapse.

The present situation is slowly clarifying, as described in a recent paper by Schlosshauer as follows:

Several decoherence-unrelated proposals have been put forward in the past to elucidate the meaning of probabilities and arrive at the Born rule … It is fair to say that no decisive conclusion appears to have been reached as to the success of these derivations. …

As it is well known, [many papers by Bohr insist upon] the fundamental role of classical concepts. The experimental evidence for superpositions of macroscopically distinct states on increasingly large length scales counters such a dictum. Only the physical interactions between systems then determine a particular decomposition into classical states from the view of each particular system. Thus classical concepts are to be understood as locally emergent in a relative-state sense and should no longer claim a fundamental role in the physical theory.

References and notes

Further reading

• R. Buniy, S. Hsu and A. Zee On the origin of probability in quantum mechanics (2006)

See also

• Measurement in quantum mechanics
• Philosophy of physics
• Quantum Zeno effect
• Objective collapse theory
• Wave function collapse
• Ghirardi-Rimini-Weber theory
• Quantum decoherence
• EPR paradox
• Quantum pseudo-telepathy

External links

• The Quantum Measurement Problem Two presentations: a non-technical and a more technical presentation.

Predefinição:Quantum mechanics Predefinição:Twootheruses

Historically, in physics, hidden variable theories were espoused by a minority of physicists who argued that the statistical nature of quantum mechanics indicated that quantum mechanics is "incomplete". Albert Einstein, the most famous proponent of hidden variables, insisted that, "I am convinced God does not play dice" — meaning that he believed that physical theories must be deterministic to be complete. Later, Bell's theorem would prove (in the opinion of most physicists and contrary to Einstein's assertion) that local hidden variables are impossible. It was thought that if hidden variables exist, new physical phenomena beyond quantum mechanics are needed to explain the universe as we know it.

The most famous such theory (because it gives the same answers as quantum mechanics, thus invalidating the famous theorem by von Neumann that no hidden variable theory reproducing the statistical predictions of QM is possible) is that of David Bohm. It is most commonly known as the Bohm interpretation or the Causal Interpretation of quantum mechanics. Bohm's (nonlocal) hidden variable is called the quantum potential. Nowadays Bohm's theory is considered to be one of many interpretations of quantum mechanics which give a realist interpretation, and not merely a positivistic one, to quantum-mechanical calculations. It is in fact just a reformulation of conventional quantum mechanics obtained by rearranging the equations and renaming the variables. Nevertheless it is a hidden variable theory.

The major reference for Bohm's theory today is his posthumous book with Basil Hiley.

Motivation

Quantum mechanics is nondeterministic, meaning that it generally does not predict the outcome of any measurement with certainty. Instead, it tells us what the probabilities of the outcomes are. This leads to the situation where measurements of a certain property done on two apparently identical systems can give different answers. The question arises whether there might be some deeper reality hidden beneath quantum mechanics, to be described by a more fundamental theory that can always predict the outcome of each measurement with certainty. In other words if the exact properties of every subatomic particle and smaller were known the entire system could be modeled exactly using deterministic physics similar to classical physics.

In other words, quantum mechanics as it stands might be an incomplete description of reality. Some physicists maintain that underlying the probabilistic nature of the universe is an objective foundation/property — the hidden variable. Others, however, believe that there is no deeper reality in quantum mechanics — experiments have shown a vast class of hidden variable theories to be incompatible with observations.[ref please]

Although determinism was initially a major motivation for physicists looking for hidden variable theories, nondeterministic theories trying to explain what the supposed reality underlying the quantum mechanics formalism looks like are also considered hidden variable theories; for example Edward Nelson's stochastic mechanics.

EPR Paradox & Bell's Theorem

In 1935, Einstein, Podolsky and Rosen wrote a four-page paper titled "Can quantum-mechanical description of physical reality be considered complete?" that argued that such a theory was in fact necessary, proposing the EPR Paradox as proof. In 1964, John Bell showed through his famous theorem that if local hidden variables exist, certain experiments could be performed where the result would satisfy a Bell inequality. If, on the other hand, Quantum entanglement is correct the Bell inequality would be violated. Another no-go theorem concerning hidden variable theories is the Kochen-Specker theorem.

Physicists such as Alain Aspect and Paul Kwiat have performed experiments that have found violations of these inequalities up to 242 standard deviations(excellent scientific certainty). This rules out local hidden variable theories, but does not rule out non-local ones (which would refute quantum entanglement). Theoretically, there could be experimental problems that affect the validity of the experimental findings.

Some hidden-variable theories

A hidden-variable theory which is consistent with quantum mechanics would have to be non-local, maintaining the existence of instantaneous or faster than light noncausal relations (correlations) between physically separated entities. The first hidden-variable theory was the pilot wave theory of Louis de Broglie, dating from the late 1920s. The currently best-known hidden-variable theory, the Causal Interpretation, of the physicist and philosopher David Bohm, created in 1952, is a non-local hidden variable theory. Those who believe the Bohm interpretation to be actually true (rather than a mere model or interpretation), and the quantum potential to be real, refer to Bohmian mechanics.

What Bohm did, on the basis of an idea of Louis de Broglie, was to posit both the quantum particle, e.g. an electron, and a hidden 'guiding wave' that governs its motion. Thus, in this theory electrons are quite clearly particles. When you perform a double-slit experiment (see wave-particle duality), they go through one slit rather than the other. However, their choice of slit is not random but is governed by the guiding wave, resulting in the wave pattern that is observed.

Such a view does not contradict the idea of local events that is used in both classical atomism and relativity theory as Bohm's theory (and indeed quantum mechanics, with which it is exactly equivalent) are still locally causal but allow nonlocal correlations (that is information travel is still restricted to the speed of light). It points to a view of a more holistic, mutually interpenetrating and interacting world. Indeed Bohm himself stressed the holistic aspect of quantum theory in his later years, when he became interested in the ideas of Jiddu Krishnamurti. The Bohm interpretation (as well as others) has also been the basis of some books which attempt to connect physics with Eastern mysticism and consciousness{{carece de fontes}}. Nevertheless this nonlocality is seen as a weakness of Bohm's theory by some physicists{{carece de fontes}}.

Another possible weakness of Bohm's theory is that some feel that it looks contrived{{carece de fontes}}. It was deliberately designed to give predictions which are in all details identical to conventional quantum mechanics{{carece de fontes}}. Bohm's aim was not to make a serious counterproposal but simply to demonstrate that hidden-variable theories are indeed possible{{carece de fontes}}. His hope was that this could lead to new insights and experiments that would lead beyond the current quantum theories{{carece de fontes}}.

Another type of deterministic theory was recently introduced by Gerard 't Hooft. This theory is motivated by the problems that are encountered when one tries to formulate a unified theory of quantum gravity.

References

See also

• Local hidden variable theory
• Bell's theorem
• Bell test experiments
• Quantum mechanics
• Bohm interpretation

Category:Quantum measurement * pt:Teoria das variáveis ocultas

In quantum mechanics, a local hidden variable theory is one in which distant events are assumed to have no instantaneous (or at least faster-than-light) effect on local ones. According to the quantum entanglement theory of quantum mechanics, on the other hand, distant events may under some circumstances have instantaneous correlations with local ones. As a result of this it is now generally accepted that there can be no interpretations of quantum mechanics which use local hidden variables. (There are those who dispute this. Their arguments are called loophole theories, referring to loopholes in the presuppositions of Bell's local hidden variable theory, implying Bell's theorem to be not sufficiently general to draw general conclusions from it with respect to locality or nonlocality of the quantum world.) The term is most often used in discussions of the EPR paradox and Bell's inequalities. It is effectively synonymous with the concept of local realism, which can only correctly be applied to classical physics and not to quantum mechanics.

Local hidden variables and the Bell tests

The principle of "locality" enables the assumption to be made in Bell test experiments that the probability of a coincidence can be written in factorised form:

(1) $P(a,b)=\int d\lambda \cdot \rho (\lambda )\cdot p_{A}(a,\lambda )\cdot p_{B}(b,\lambda )$

where $p_{A}(a,\lambda )$ is the probability of detection of particle A with hidden variable λ by detector A, set in direction a, and similarly p_B (b, λ) is the probability at detector B for particle B, sharing the same value of λ. The source is assumed to produce particles in the state λ with probability $\rho (\lambda )$.

Using (1), various "Bell inequalities" can be derived, giving restrictions on the possible behaviour of local hidden variable models.

When John Bell originally derived his inequality, it was in relation to pairs of indivisible "spin-1/2" particles, every one of those emitted being detected. In these circumstances it is found that local realist assumptions lead to a straight line prediction for the relationship between quantum correlation and the angle between the settings of the two detectors. It was soon realised, however, that real experiments were not feasible with spin-1/2 particles. They were conducted instead using photons. The local hidden variable prediction for these is not a straight line but a sine curve, similar to the quantum mechanical prediction but of only half the "visibility".

The difference between the two predictions is due to the different functions $p_{A}(a,\lambda )$ and $p_{B}(a,\lambda )$ involved. By assuming different functions, a great variety of other realist predictions can be derived, some very close to the quantum-mechanical one. The choice of function, however, is not arbitrary. In optical experiments using polarisation, for instance, the natural assumption is that it is a cosine-squared function, corresponding to adherence to Malus's Law.

Bell tests with no "non-detections"

Consider, for example, David Bohm's thought-experiment (Bohm, 1951), in which a molecule breaks into two atoms with opposite spins. Assume this spin can be represented by a real vector, pointing in any direction. It will be the "hidden variable" in our model. Taking it to be a unit vector, all possible values of the hidden variable are represented by all points on the surface of a unit sphere.

Suppose the spin is to be measured in the direction a. Then the natural assumption, given that all atoms are detected, is that all atoms the projection of whose spin in the direction a is positive will be detected as spin up (coded as +1) while all whose projection is negative will be detected as spin down (coded as −1). The surface of the sphere will be divided into two regions, one for +1, one for −1, separated by a great circle in the plane perpendicular to a. Assuming for convenience that a is horizontal, corresponding to the angle a with respect to some suitable reference direction, the dividing circle will be in a vertical plane. So far we have modelled side A of our experiment.

Now to model side B. Assume that b too is horizontal, corresponding to the angle b. There will be second great circle drawn on the same sphere, to one side of which we have +1, the other −1 for particle B. The circle will be again be in a vertical plane.

The two circles divide the surface of the sphere into four regions. The type of "coincidence" (++, −−, +− or −+) observed for any given pair of particles is determined by the region within which their hidden variable falls. Assuming the source to be "rotationally invariant" (to produce all possible states λ with equal probability), the probability of a given type of coincidence will clearly be proportional to the corresponding area, and these areas will vary linearly with the angle between a and b. (To see this, think of an orange and its segments. The area of peel corresponding to a number n of segments is roughly proportional to n. More accurately, it is proportional to the angle subtended at the centre.)

The formula (1) above has not been used explicitly — it is hardly relevant when, as here, the situation is fully deterministic. The problem could be reformulated in terms of the functions in the formula, with ρ constant and the probability functions step functions. The principle behind (1) has in fact been used, but purely intuitively.

Ficheiro:StraightLines.png

Fig. 1: The realist prediction (solid lines) for quantum correlation when there are no non-detections. The quantum-mechanical prediction is the dotted curve.

Thus the local hidden variable prediction for the probability of coincidence is proportional to the angle (b − a) between the detector settings. The quantum correlation is defined to be the expectation value of the product of the individual outcomes, and this is

(2)    E = P₊₊ + P₋₋ − P₊₋ − P₋₊

where P₊₊ is the probability of a '+' outcome on both sides, P₊₋ that of a + on side A, a '−' on side B, etc..

Since each individual term varies linearly with the difference (b − a), so does their sum.

The result is shown in fig. 1.

Optical Bell tests

In almost all real applications of Bell's inequalities, the particles used have been photons. It is not necessarily assumed that the photons are particle-like. They may be just short pulses of classical light (Clauser, 1978). It is not assumed that every single one is detected. Instead the hidden variable set at the source is taken to determine only the probability of a given outcome, the actual individual outcomes being partly determined by other hidden variables local to the analyser and detector. It is assumed that these other hidden variables are independent on the two sides of the experiment (Clauser, 1974; Bell, 1971).

In this "stochastic" model, in contrast to the above deterministic case, we do need equation (1) to find the local realist prediction for coincidences. It is necessary first to make some assumption regarding the functions $p_{A}(a,\lambda )$ and $p_{B}(a,\lambda )$, the usual one being that these are both cosine-squares, in line with Malus' Law. Assuming the hidden variable to be polarisation direction (parallel on the two sides in real applications, not orthogonal), equation (1) becomes:

(3) $P(a,b)=\int d\lambda \cdot \rho (\lambda )\cdot \cos ^{2}(a-\lambda )\cdot \cos ^{2}(b-\lambda )={\frac {1}{8}}+{\frac {\cos ^{2}\phi }{4}}$, where $\phi =b-a$.

The predicted quantum correlation can be derived from this and is shown in fig. 2.

Fig. 2: The realist prediction (solid curve) for quantum correlation in an optical Bell test. The quantum-mechanical prediction is the dotted curve.

In optical tests, incidentally, it is not certain that the quantum correlation is well-defined. Under a classical model of light, a single photon can go partly into the '+' channel, partly into the '−' one, resulting in the possibility of simultaneous detections in both. Though experiments such as Grangier et al.'s (Grangier, 1986) have shown that this probability is very low, it is not logical to assume that it is actually zero. The definition of quantum correlation is adapted to the idea that outcomes will always be +1, −1 or 0. There is no obvious way of including any other possibility, which is one of the reasons why Clauser and Horne's 1974 Bell test, using single-channel polarisers, should be used instead of the CHSH Bell test. The "CH74" inequality concerns just probabilities of detection, not quantum correlations.

Generalizations of the models

By varying the assumed probability and density functions in equation (1) we can arrive at a considerable variety of local realist predictions.

Time effects

Previously some new hypotheses were conjectured concerning the role of time in constructing hidden variables theory. One approach is suggested by K. Hess and W. Philipp (Hess, 2002) and discusses possible consequences of time dependences of hidden variables, previously not taken into account by Bell's theorem. This hypothesis has been criticized by R.D. Gill, G. Weihs, A. Zeilinger and M. Żukowski (Gill, 2002).

Another hypothesis suggests to review the notion of physical time (Kurakin, 2004). Hidden variables in this concept evolve in so called 'hidden time', not equivalent to physical time. Physical time relates to 'hidden time' by some 'sewing procedure'. This model stays physically non-local, though the locality is achieved in mathematical sense.

Optical models deviating from Malus' Law

If we make realistic (wave-based) assumptions regarding the behaviour of light on encountering polarisers and photodetectors, we find that we are not compelled to accept that the probability of detection will reflect Malus' Law exactly.

We might perhaps suppose the polarisers to be perfect, with output intensity of polariser A proportional to cos²(a − λ), but reject the quantum-mechanical assumption that the function relating this intensity to the probability of detection is a straight line through the origin. Real detectors, after all, have "dark counts" that are there even when the input intensity is zero, and become saturated when the intensity is very high. It is not possible for them to produce outputs in exact proportion to input intensity for all intensities.

By varying our assumptions, it seems possible that the realist prediction could approach the quantum-mechanical one within the limits of experimental error (Marshall, 1983), though clearly a compromise must be reached. We have to match both the behaviour of the individual light beam on passage through a polariser and the observed coincidence curves. The former would be expected to follow Malus' Law fairly closely, though experimental evidence here is not so easy to obtain. We are interested in the behaviour of very weak light and the law may be slightly different from that of stronger light.

References

• Bell, 1971: J. S. Bell, in Foundations of Quantum Mechanics, Proceedings of the International School of Physics “Enrico Fermi”, Course XLIX, B. d’Espagnat (Ed.) (Academic, New York, 1971), p. 171 and Appendix B. Pages 171-81 are reproduced as Ch. 4, pp 29–39, of J. S. Bell, Speakable and Unspeakable in Quantum Mechanics (Cambridge University Press 1987)
• Bohm, 1951: D. Bohm, Quantum Theory, Prentice-Hall 1951
• Clauser, 1974: J. F. Clauser and M. A. Horne, Experimental consequences of objective local theories, Physical Review D, 10, 526-35 (1974)
• Clauser, 1978: J. F. Clauser and A. Shimony, Bell’s theorem: experimental tests and implications, Reports on Progress in Physics 41, 1881 (1978)
• Gill, 2002: R.D. Gill, G. Weihs, A. Zeilinger and M. Żukowski, No time loophole in Bell's theorem; the Hess-Philipp model is non-local, quant-ph/0208187 (2002)
• Grangier, 1986: P. Grangier, G. Roger and A. Aspect, Experimental evidence for a photon anticorrelation effect on a beam splitter: a new light on single-photon interferences, Europhysics Letters 1, 173–179 (1986)
• Hess, 2002: K. Hess and W. Philipp, Europhys. Lett., 57:775 (2002)
• Kurakin, 2004: Pavel V. Kurakin, Hidden variables and hidden time in quantum theory, a preprint #33 by Keldysh Inst. of Appl. Math., Russian Academy of Sciences (2004)
• Marshall, 1983: T. W. Marshall, E. Santos and F. Selleri, Local Realism has not been Refuted by Atomic-Cascade Experiments, Physics Letters A, 98, 5–9 (1983)

See also

• Hidden variable theory

Predefinição:Otheruses4

In physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. Quantum mechanics predicts through Bell's inequality the direct violation of this principle. Experiments have shown that quantum mechanically entangled particles violate this principle: they have been shown to influence each other when physically separated by 18 km, thus the principle of locality is false.

Einstein's View

EPR Paradox

Albert Einstein felt that there was something fundamentally incorrect with quantum mechanics since it predicted violations of locality. In a famous paper he and his co-authors articulated the Einstein-Podolsky-Rosen Paradox. Thirty years later John Stewart Bell responded with a paper which stated (paraphrased) that no physical theory of local hidden variables can ever reproduce all of the predictions of quantum mechanics (Bell's theorem).

Philosophical View

Einstein assumed that principle of locality was necessary, and there could be no violations of it. He said:

“ The following idea characterises the relative independence of objects far apart in space A and B: external influence on A has no direct influence on B; this is known as the Principle of Local Action, which is used consistently only in field theory. If this axiom were to be completely abolished, the idea of the existence of quasienclosed systems, and thereby the postulation of laws which can be checked empirically in the accepted sense, would become impossible. ”

Local Realism

Local realism is the combination of the principle of locality with the "realistic" assumption that all objects must objectively have pre-existing values for any possible measurement before these measurements are made. Einstein liked to say that the Moon is "out there" even when no one is observing it.

Realism

Realism in the sense used by physicists does not directly equate to realism in metaphysics. The latter is the claim that there is in some sense a mind-independent world. Even if the results of a possible measurement do not pre-exist the measurement, that does not mean they are the creation of the observer (as in the "consciousness causes collapse" interpretation of quantum mechanics). Furthermore, a mind-independent property does not have to be the value of some physical variable such as position or momentum. A property can be dispositional, i.e. it can be a tendency, in the way that glass objects tend to break, or are disposed to break, even if they do not actually break. Likewise, the mind-independent properties of quantum systems could consist of a tendency to respond to certain measurements with certain values with some probability. Such an ontology would be metaphysically realistic without being realistic in the physicist's sense of "local realism" (which would require that single value be produced with certainty).

Local realism is a significant feature of classical mechanics, general relativity and Maxwell's theory, but quantum mechanics largely rejects this principle due to the presence of distant quantum entanglements, most clearly demonstrated by the EPR paradox and quantified by Bell's inequalities. Any theory, like quantum mechanics, that violates Bell's inequalities must abandon either local realism or counterfactual definiteness. (Some physicists dispute that experiments have demonstrated Bell's violations, on the grounds that the sub-class of inhomogeneous Bell inequalities has not been tested or other experimental limitations). Different interpretations of quantum mechanics reject different parts of local realism and/or counterfactual definiteness.

Copenhagen interpretation

In most of the conventional interpretations, such as the version of the Copenhagen interpretation and the interpretation based on Consistent Histories, where the wavefunction is not assumed to have a direct physical interpretation of reality, it is realism that is rejected. The actual definite properties of a physical system "do not exist" prior to the measurement, and the wavefunction has a restricted interpretation as nothing more than a mathematical tool used to calculate the probabilities of experimental outcomes, in agreement with positivism in philosophy as the only topic that science should discuss.

In the version of the Copenhagen interpretation where the wavefunction is assumed to have a physical interpretation of reality (the nature of which is unspecified) the principle of locality is violated during the measurement process via wavefunction collapse. This is a non-local process because Born's Rule, when applied to the system's wave function, yields a probability density for all regions of space and time. Upon measurement of the physical system, the probability density vanishes everywhere instantaneously, except where (and when) the measured entity is found to exist. This "vanishing" would be a real physical process, and clearly non-local (faster than light) if the wave function is considered physically real and the probability density converged to zero at arbitrarily far distances during the finite time required for the measurement process.

Bohm interpretation

The Bohm interpretation always wants to preserve realism, and it needs to violate the principle of locality to achieve the required correlations.

Many-worlds interpretation

In the many-worlds interpretation realism and locality are retained but counterfactual definiteness is rejected by the extension of the notion of reality to allow the existence of parallel universes.

Because the differences between the different interpretations are mostly philosophical ones (except for the Bohm and many-worlds interpretations), physicists usually use the language in which the important statements are independent of the interpretation we choose. In this framework, only the measurable action at a distance - a superluminal propagation of real, physical information - would usually be considered in violation of locality by physicists. Such phenomena have never been seen, and they are not predicted by the current theories (with the possible exception of the Bohm theory).

Relativity

Locality is one of the axioms of relativistic quantum field theory, as required for causality. The formalization of locality in this case is as follows: if we have two observables, each localized within two distinct space-time regions which happen to be at a spacelike separation from each other, the observables must commute. Alternatively, a solution to the field equations is local if the underlying equations are either Lorentz invariant or, more generally, generally covariant or locally Lorentz invariant.

Notes

See also

• EPR paradox
• Local hidden variable theory
• Nonlocality

For a non-technical introduction to the topic, please see Introduction to quantum mechanics.

In physics, especially quantum mechanics, the Schrödinger equation is an equation that describes how the quantum state of a physical system changes in time. It is as central to quantum mechanics as Newton's laws are to classical mechanics.

In the standard interpretation of quantum mechanics, the quantum state, also called a wavefunction or state vector, is the most complete description that can be given to a physical system. Solutions to Schrödinger's equation describe not only atomic and subatomic systems, electrons and atoms, but also macroscopic systems, possibly even the whole universe. The equation is named after Erwin Schrödinger, who discovered it in 1926.

Schrödinger's equation can be mathematically transformed into Heisenberg's matrix mechanics, and into Feynman's path integral formulation. The Schrödinger equation describes time in a way that is inconvenient for relativistic theories, a problem which is not as severe in Heisenberg's formulation and completely absent in the path integral.

The Schrödinger equation

The Schrödinger equation takes several different forms, depending on the physical situation. This section presents the equation for the general case and for the simple case encountered in many textbooks.

General quantum system

For a general quantum system:

$i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,\,t)={\hat {H}}\Psi (\mathbf {r} ,\,t)$

where

• $i\$ is the imaginary unit
• $\Psi (\mathbf {r} ,\,t)$ is the wave function, which is the probability amplitude for different configurations of the system.
• $\scriptstyle \hbar$ hbar is the Reduced Planck's constant, (Planck's constant divided by $2\pi$), and it can be set to a value of 1 when using natural units.
• $\scriptstyle {\hat {H}}$ is the Hamiltonian operator.

Single particle in three dimensions

For a single particle in three dimensions:

$i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,\,t)=-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi (\mathbf {r} ,\,t)+V(\mathbf {r} )\Psi (\mathbf {r} ,\,t)$

where

• $\mathbf {r} =(x,y,z)$ is the particle's position in three-dimensional space,
• $\Psi (\mathbf {r} ,t)$ is the wavefunction, which is the amplitude for the particle to have a given position r at any given time t.
• $m$ is the mass of the particle.
• $V(\mathbf {r} )$ is the time independent potential energy of the particle at each position r.

Historical background and development

Ver artigo principal: Theoretical and experimental justification for the Schrödinger equation

Einstein interpreted Planck's quanta as photons, particles of light, and proposed that the energy of a photon is proportional to its frequency, a mysterious wave-particle duality. Since energy and momentum are related in the same way as frequency and wavenumber in relativity, it followed that the momentum of a photon is proportional to its wavenumber.

DeBroglie hypothesized that this is true for all particles, for electrons as well as photons, that the energy and momentum of an electron are the frequency and wavenumber of a wave. Assuming that the waves travel roughly along classical paths, he showed that they form standing waves only for certain discrete frequencies, discrete energy levels which reproduced the old quantum condition.

Following up on these ideas, Schrödinger decided to find a proper wave equation for the electron. He was guided by Hamilton's analogy between mechanics and optics, encoded in the observation that the zero-wavelength limit of optics resembles a mechanical system--- the trajectories of light rays become sharp tracks which obey an analog of the principle of least action. Hamilton believed that mechanics was the zero-wavelength limit of wave propagation, but did not formulate an equation for those waves. This is what Schrödinger did, and a modern version of his reasoning is reproduced in the next section. The equation he found is (in natural units):

$i{\frac {\partial }{\partial t}}\Psi (x,\,t)=-{\frac {1}{2m}}\nabla ^{2}\Psi (x,\,t)+V(x)\Psi (x,\,t).$

Using this equation, Schrödinger computed the spectral lines for hydrogen by treating a hydrogen atom's single negatively charged electron as a wave, $\Psi (x,\,t)\;$, moving in a potential well, V, created by the positively charged proton. This computation reproduced the energy levels of the Bohr model.

But this was not enough, since Sommerfeld had already seemingly correctly reproduced relativistic corrections. Schrödinger used the relativistic energy momentum relation to find what is now known as the Klein-Gordon equation in a Coulomb potential:

$\left(E+{e^{2} \over r}\right)^{2}\psi (x)=-\nabla ^{2}\psi (x)+m^{2}\psi (x).$

He found the standing-waves of this relativistic equation, but the relativistic corrections disagreed with Sommerfeld's formula. Discouraged, he put away his calculations and secluded himself in an isolated mountain cabin with a lover.{{carece de fontes}}

While there, Schrödinger decided that the earlier nonrelativistic calculations were novel enough to publish, and decided to leave off the problem of relativistic corrections for the future. He put together his wave equation and the spectral analysis of hydrogen in a paper in 1926. The paper was enthusiastically endorsed by Einstein, who saw the matter-waves as the visualizable antidote to what he considered to be the overly formal matrix mechanics.

The Schrödinger equation tells you the behaviour of $\psi$, but does not say what $\psi$ is. Schrödinger tried unsuccessfully, in his fourth paper, to interpret it as a charge density. In 1926 Max Born, just a few days after Schrödinger's fourth and final paper was published, successfully interpreted $\psi$ as a probability amplitude. Schrödinger, though, always opposed a statistical or probabilistic approach, with its associated discontinuities; like Einstein, who believed that quantum mechanics was a statistical approximation to an underlying deterministic theory, Schrödinger was never reconciled to the Copenhagen interpretation.

Derivation

Short heuristic derivation

Assumptions

(1) The total energy E of a particle is

$E=T+V={\frac {p^{2}}{2m}}+V$

This is the classical expression for a particle with mass m where the total energy E is the sum of the kinetic energy $T\$, ${\frac {p^{2}}{2m}}$, and the potential energy V. The momentum of the particle is p, or mass times velocity. The potential energy is assumed to vary with position, and possibly time as well.

Note that the energy E and momentum p appear in the following two relations:

(2) Einstein's light quanta hypothesis of 1905, which asserts that the energy E of a photon is proportional to the frequency f of the corresponding electromagnetic wave:

$E=hf={h \over 2\pi }(2\pi f)=\hbar \omega \;$

where the frequency f of the quanta of radiation (photons) are related by Planck's constant h,

and $\omega =2\pi f\;$ is the angular frequency of the wave.

(3) The de Broglie hypothesis of 1924, which states that any particle can be associated with a wave, represented mathematically by a wavefunction Ψ, and that the momentum p of the particle is related to the wavelength λ of the associated wave by:

$p={h \over \lambda }={h \over 2\pi }{2\pi \over \lambda }=\hbar k\;$

where $\lambda \,$ is the wavelength and $k=2\pi /\lambda \;$ is the wavenumber of the wave.

Expressing p and k as vectors, we have

$\mathbf {p} =\hbar \mathbf {k} \;$

Expressing the wave function as a complex plane wave

Schrödinger's great insight, late in 1925, was to express the phase of a plane wave as a complex phase factor:

$\Psi (\mathbf {x} ,t)=Ae^{i(\mathbf {k} \cdot \mathbf {x} -\omega t)}$

and to realize that since

${\frac {\partial }{\partial t}}\Psi =-i\omega \Psi$

then

$E\Psi =\hbar \omega \Psi =i\hbar {\frac {\partial }{\partial t}}\Psi$

and similarly since

${\frac {\partial }{\partial x}}\Psi =ik_{x}\Psi$

and

${\frac {\partial ^{2}}{\partial x^{2}}}\Psi =-k_{x}^{2}\Psi$

we find:

$p_{x}^{2}\Psi =(\hbar k_{x})^{2}\Psi =-\hbar ^{2}{\frac {\partial ^{2}}{\partial x^{2}}}\Psi$

so that, again for a plane wave, he obtained:

$p^{2}\Psi =(p_{x}^{2}+p_{y}^{2}+p_{z}^{2})\Psi =-\hbar ^{2}\left({\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}\right)\Psi =-\hbar ^{2}\nabla ^{2}\Psi$

And by inserting these expressions for the energy and momentum into the classical formula we started with we get Schrödinger's famed equation for a single particle in the 3-dimensional case in the presence of a potential V:

$i\hbar {\frac {\partial }{\partial t}}\Psi =-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi +V\Psi$

Longer discussion

The particle is described by a wave, and in natural units, the frequency is the energy E of the particle, while the momentum p is the wavenumber k. These are not two separate assumptions, because of special relativity.

$E=\omega \;\;\;\;p=k\,$

The total energy is the same function of momentum and position as in classical mechanics:

$E=T(p)+V(x)={p^{2} \over 2m}+V(x)$

where the first term T(p) is the kinetic energy and the second term V(x) is the potential energy.

Schrödinger required that a Wave packet at position x with wavenumber k will move along the trajectory determined by Newton's laws in the limit that the wavelength is small.

Consider first the case without a potential, V=0.

$E={1 \over 2m}(p_{x}^{2}+p_{y}^{2}+p_{z}^{2})$

$\omega ={1 \over 2m}(k_{x}^{2}+k_{y}^{2}+k_{z}^{2})$

So that a plane wave with the right energy/frequency relationship obeys the free Schrödinger equation:

$i{\partial \over \partial t}\Psi =-{1 \over 2m}\left({\partial ^{2}\Psi \over \partial x^{2}}+{\partial ^{2}\Psi \over \partial y^{2}}+{\partial ^{2}\Psi \over \partial z^{2}}\right)$

and by adding together plane waves, you can make an arbitrary wave.

When there is no potential, a wavepacket should travel in a straight line at the classical velocity. The velocity v of a wavepacket is:

$v={\partial \omega \over \partial k}={\partial \over \partial k}{k^{2} \over 2m}={k \over m}$

which is the momentum over the mass as it should be. This is one of Hamilton's equations from mechanics:

${dx \over dt}={\partial H \over \partial p}$

after identifying the energy and momentum of a wavepacket as the frequency and wavenumber.

To include a potential energy, consider that as a particle moves the energy is conserved, so that for a wavepacket with approximate wavenumber k at approximate position x the quantity

${k^{2} \over 2m}+V(x)$

must be constant. The frequency doesn't change as a wave moves, but the wavenumber does. So where there is a potential energy, it must add in the same way:

$i{\partial \over \partial t}\Psi =-{1 \over 2m}\nabla ^{2}\Psi +V(x)\Psi$

This is the time dependent Schrödinger equation. It is the equation for the energy in classical mechanics, turned into a differential equation by substituting:

$E\rightarrow i{\partial \over \partial t}\;\;\;\;\;\;p\rightarrow -i{\partial \over \partial x}$

Schrödinger studied the standing wave solutions, since these were the energy levels. Standing waves have a complicated dependence on space, but vary in time in a simple way:

$\Psi (x,t)=\psi (x)e^{-iEt}\,$

substituting, the time-dependent equation becomes the standing wave equation:

${E}\psi (x)=-{1 \over 2m}\nabla ^{2}\psi (x)+V(x)\psi (x)$

Which is the original time-independent Schrödinger equation.

In a potential gradient, the k-vector of a short-wavelength wave must vary from point to point, to keep the total energy constant. Sheets perpendicular to the k-vector are the wavefronts, and they gradually change direction, because the wavelength is not everywhere the same. A wavepacket follows the shifting wavefronts with the classical velocity, with the acceleration equal to the force divided by the mass.

an easy modern way to verify that Newton's second law holds for wavepackets is to take the Fourier transform of the time dependent Schrödinger equation. For an arbitrary polynomial potential this is called the Schrödinger equation in the momentum representation:

$i{\partial \Psi (p,\,t) \over \partial t}={p^{2} \over 2m}\Psi (p,\,t)+V(i{\partial \over \partial p})\Psi (p,\,t)$

The group-velocity relation for the fourier transformed wave-packet gives the second of Hamilton's equations.

${dp \over dt}=-{\partial H \over \partial x}$

Versions

There are several equations which go by Schrödinger's name:

Time dependent equation

This is the equation of motion for the quantum state. In the most general form, it is written:

$i\hbar {\partial \over \partial t}\Psi (x,\,t)={\hat {H}}\Psi (x,\,t)$

Where ${\hat {H}}$ is a linear operator acting on the wavefunction $\Psi$. ${\hat {H}}$ takes as input one $\Psi$ and produces another in a linear way, a function-space version of a matrix multiplying a vector. For the specific case of a single particle in one dimension moving under the influence of a potential V (adopting natural units where $\scriptstyle \hbar =1$):

$i{\partial \over \partial t}\Psi (x,\,t)=-{1 \over 2m}{\partial ^{2} \over \partial x^{2}}\Psi (x,\,t)+V(x)\Psi (x,\,t)\,$

and the operator H can be read off:

${\hat {H}}=-{1 \over 2m}{\partial ^{2} \over \partial x^{2}}+V(x)\,$

it is a combination of the operator which takes the second derivative, and the operator which pointwise multiplies $\Psi$ by V(x). When acting on $\Psi$ it reproduces the right hand side.

For a particle in three dimensions, the only difference is more derivatives:

$i{\partial \over \partial t}\Psi (x,\,t)=-{1 \over 2m}\nabla ^{2}\Psi (x,\,t)+V(x)\Psi (x,\,t)\,$

and for N particles, the difference is that the wavefunction is in 3N-dimensional configuration space, the space of all possible particle positions.

$i{\partial \over \partial t}\Psi (x_{1},...,x_{n},t)=(-{\nabla _{1}^{2} \over 2m_{1}}-{\nabla _{2}^{2} \over 2m_{2}}...-{\nabla _{N}^{2} \over 2m_{N}})\Psi (x_{1},...,x_{n},t)+V(x_{1},..,x_{N},t)\Psi (x_{1},...,x_{n},t)\,$

This last equation is in a very high dimension, so that the solutions are not easy to visualize.

Time independent equation

This is the equation for the standing waves, the eigenvalue equation for H. In abstract form, for a general quantum system, it is written:

${\hat {H}}\psi =E\cdot \psi \,$

For a particle in one dimension,

$E\psi =-{\frac {\hbar ^{2}}{2m}}{\partial ^{2}\psi \over \partial x^{2}}+V(x)\psi \,$

But there is a further restriction--- the solution must not grow at infinity, so that it has a finite L^2-norm:

$\|\psi \|^{2}=\int |\psi (x)|^{2}\,dx\,$

For example, when there is no potential, the equation reads:

$-E\psi ={\frac {\hbar ^{2}}{2m}}{\partial ^{2}\psi \over \partial x^{2}}\,$

which has oscillatory solutions for E>0 (the C's are arbitrary constants):

$\psi _{E}(x)=C_{1}e^{i{\sqrt {2mE/\hbar ^{2}}}\,x}+C_{2}e^{-i{\sqrt {2mE/\hbar ^{2}}}\,x}\,$

and exponential solutions for E<0

$\psi _{-|E|}(x)=C_{1}e^{{\sqrt {2m|E|/\hbar ^{2}}}\,x}+C_{2}e^{-{\sqrt {2m|E|/\hbar ^{2}}}\,x}\,$

The exponentially growing solutions have an infinite norm, and are not physical. They are not allowed in a finite volume with periodic or fixed boundary conditions.

For a constant potential V the solution is oscillatory for E>V and exponential for E<V, corresponding to energies which are allowed or disallowed in classical mechnics. Oscillatory solutions have a classically allowed energy and correspond to actual classical motions, while the exponential solutions have a disallowed energy and describe a small amount of quantum bleeding into the classically disallowed region, to quantum tunneling. If the potential V grows at infinity, the motion is classically confined to a finite region, which means that in quantum mechanics every solution becomes an exponential far enough away. The condition that the exponential is decreasing restricts the energy levels to a discrete set, called the allowed energies.

Energy eigenstates

A solution $\psi _{E}(x)$ of the time independent equation is called an energy eigenstate with energy E:

$H\psi _{E}=E\psi _{E}\,$

To find the time dependence of the state, consider starting the time-dependent equation with an initial condition $\psi _{E}(x)$. The time derivative at t=0 is everywhere proportional to the value:

$\left.i\hbar {\partial \over \partial t}\Psi (x,\,t)\right|_{t=0}=\left.H\Psi (x,\,t)\right|_{t=0}=E\Psi (x,\,0)\,$

So that at first the whole function just gets rescaled, and it maintains the property that its time derivative is proportional to itself. So for all times,

$\Psi (x,\,t)=A(t)\psi _{E}(x)\,$

substituting,

$i\hbar {dA \over dt}=-EA\,$

So that the solution of the time-dependent equation with this initial condition is:

$\Psi (x,\,t)=\psi _{E}(x)e^{-i{Et/\hbar }}\,$

This is a restatement of the fact that solutions of the time-independent equation are the standing wave solutions of the time dependent equation. They only get multiplied by a phase as time goes by, and otherwise are unchanged.

Superpositions of energy eigenstates change their properties according to the relative phases between the energy levels.

Nonlinear equation

The nonlinear Schrödinger equation is the partial differential equation

$i\partial _{t}\psi =-{1 \over 2}\partial _{x}^{2}\psi +\kappa |\psi |^{2}\psi$

for the complex field ψ.

This equation arises from the Hamiltonian

$H=\int dx\left[{1 \over 2}|\partial _{x}\psi |^{2}+{\kappa \over 2}|\psi |^{4}\right]$

with the Poisson brackets

$\{\psi (x),\psi (y)\}=\{\psi ^{*}(x),\psi ^{*}(y)\}=0\,$

$\{\psi ^{*}(x),\psi (y)\}=i\delta (x-y).\,$

It must be noted that this is a classical field equation. Unlike its linear counterpart, it never describes the time evolution of a quantum state.

Properties

First order in time

The Schrödinger equation describes the time evolution of a quantum state, and must determine the future value from the present value. A classical field equation can be second order in time derivatives, the classical state can include the time derivative of the field. But a quantum state is a full description of a system, so that the Schrödinger equation is always first order in time.

Linear

The Schrödinger equation is linear in the wavefunction: if $\Psi _{A}(x,t)$ and $\Psi _{B}(x,t)$ are solutions to the time dependent equation, then so is $a\Psi _{A}+b\Psi _{B}$, where a and b are any complex numbers.

In quantum mechanics, the time evolution of a quantum state is always linear, for fundamental reasons. Although there are nonlinear versions of the Schrödinger equation, these are not equations which describe the evolution of a quantum state, but classical field equations like Maxwell's equations or the Klein-Gordon equation.

The Schrödinger equation itself can be thought of as the equation of motion for a classical field not for a wavefunction, and taking this point of view, it describes a coherent wave of nonrelativistic matter, a wave of a Bose condensate or a superfluid with a large indefinite number of particles and a definite phase and amplitude.

Real eigenstates

The time-independent equation is also linear, but in this case linearity has a slightly different meaning. If two wavefunctions $\psi _{1}$ and $\psi _{2}$ are solutions to the time-independent equation with the same energy E, then any linear combination of the two is a solution with energy E. Two different solutions with the same energy are called degenerate.

${\hat {H}}(a\psi _{1}+b\psi _{2})=(a{\hat {H}}\psi _{1}+b{\hat {H}}\psi _{2})=E(a\psi _{1}+b\psi _{2})\,$

In an arbitrary potential, there is one obvious degeneracy: if a wavefunction $\psi$ solves the time-independent equation, so does $\psi ^{*}$. By taking linear combinations, the real and imaginary part of $\psi$ are each solutions. So that restricting attention to real valued wavefunctions does not affect the time-independent eigenvalue problem.

In the time-dependent equation, complex conjugate waves move in opposite directions. Given a solution to the time dependent equation $\Psi (x,\,t)$, the replacement:

$\Psi (x,\,t)\rightarrow \Psi ^{*}(x,\,-t)\,$

produces another solution, and is the extension of the complex conjugation symmetry to the time-dependent case. The symmetry of complex conjugation is called time-reversal.

Unitary time evolution

The Schrödinger equation is Unitary, which means that the total norm of the wavefunction, the sum of the squares of the value at all points:

$\int _{x}\Psi ^{*}(x,\,t)\Psi (x,\,t)dx=\langle \Psi |\Psi \rangle \,$

has zero time derivative.

The derivative of $\Psi ^{*}(x,\,t)$ is according to the complex conjugate equations

$-i\hbar {\partial \over \partial t}\Psi ^{*}(x,\,t)={\hat {H}}^{\dagger }\Psi ^{*}(x,\,t)\,$

where the operator $H^{\dagger }$ is defined as the continuous analog of the Hermitian conjugate,

$\langle \eta H^{\dagger }|\Psi \rangle =\langle \eta |H\Psi \rangle \,$

For a discrete basis, this just means that the matrix elements of the linear operator H obey:

${\hat {H}}_{ij}={\hat {H}}_{ji}^{*}\,$

The derivative of the inner product is:

${d \over dt}\langle \Psi |\Psi \rangle =i\langle \Psi {\hat {H}}^{\dagger }|\Psi \rangle -i\langle \Psi |H\Psi \rangle \,$

and is proportional to the imaginary part of H. If H has no imaginary part, if it is self-adjoint, then the probability is conserved. This is true not just for the Schrödinger equation as written, but for the Schrödinger equation with nonlocal hopping:

$i\hbar {\partial \over \partial t}\Psi (x,\,t)=\int _{y}H(x,y)\Psi (y,\,t)\,$

so long as:

$H(x,y)=H(y,x)^{*}\,$

the particular choice:

$H(x,y)=-{1 \over 2m}\nabla _{x}^{2}\delta (x-y)+V(x)\delta (x-y)\,$

reproduces the local hopping in the ordinary Schrödinger equation. On a discrete lattice approximation to a continuous space, H(x,y) has a simple form:

$H(x,y)=-{1 \over 2m}\,$

whenever x and y are nearest neighbors. On the diagonal

$H(x,x)=+{n \over 2m}+V(x)\,$

where n is the number of nearest neighbors.

Positivity of energy

If the potential is bounded from below, the eigenfunctions of the Schrödinger equation have energy which is also bounded from below. This can be seen most easily by using the variational principle, as follows. (See also below.)

For any linear operator $A$ bounded from below, the eigenvector with the smallest eigenvalue is the vector $\psi$ that minimizes the quantity

$\langle \psi |A|\psi \rangle$

over all $\psi$ which are normalized:

$\|\psi \|^{2}=\int _{x}|\psi (x)|^{2}=\langle \psi |\psi \rangle =1\,$

In this way, the smallest eigenvalue is expressed through the variational principle.

For the Schrödinger Hamiltonian $H$ bounded from below, the smallest eigenvalue is called the ground state energy. That energy is the minimum value of

$\langle \psi |H|\psi \rangle =\int _{x}\psi ^{*}(x)(-{\frac {1}{2m}}\nabla ^{2}\psi +V(x)\psi )=\int _{x}{\frac {1}{2m}}|\nabla \psi |^{2}+V(x)|\psi |^{2}dx$

(we used an integration by parts). The right hand side is never smaller than the smallest value of $V(x)$; in particular, the ground state energy is positive when $V(x)$ is everywhere positive.

Positive definite nondegenerate ground state

For potentials $V(x)$ that are bounded below and are not infinite in such a way that will divide space into regions which are inaccessible by quantum tunneling, there is a ground state which minimizes the integral above. The lowest energy wavefunction is real and nondegenerate and has the same sign everywhere.

To prove this, let the ground state wavefunction be $\psi$. The real and imaginary parts are separately ground states, so it is no loss of generality to assume the $\psi$ is real. Suppose now, for contradiction, that $\psi$ changes sign. Define $\eta (x)$ to be the absolute value of $\psi$.

$\eta =|\psi |$

The potential and kinetic energy integral for $\eta$ is equal to psi, except that $\eta$ has a kink wherever $\psi$ changes sign. The integrated-by-parts expression for the kinetic energy is the sum of the squared magnitude of the gradient, and it is always possible to round out the kink in such a way that the gradient gets smaller at every point, so that the kinetic energy is reduced.

This also proves that the ground state is nondegenerate. If there were two ground states $\psi _{1}(x)$ and $\psi _{2}(x)$ not proportional to each other and both everywhere nonnegative then a linear combination of the two is still a ground state, but it can be made to have a sign change.

For one-dimensional potentials, every eigenstate is nondegenerate, because the number of sign changes is equal to the level number.

Already in two dimensions, it is easy to get a degeneracy--- for example, if a particle is moving in a separable potential: V(x,y) = U(x) + W(y), then the energy levels are the sum of the energies of the one-dimensional problem. It is easy to see that by adjusting the overall scale of U and W that the levels can be made to collide.

For standard examples, the three-dimensional harmonic oscillator and the central potential, the degeneracies are a consequence of symmetry.

Completeness

The energy eigenstates form a basis--- any wavefunction may be written as a sum over the discrete energy states or an integral over continuous energy states, or more generally as an integral over a measure. This is the spectral theorem in mathematics, and in a finite state space it is just a statement of the completeness of the eigenvectors of a Hermitian matrix.

Local conservation of probability

The probability density of a particle is $\Psi ^{*}(x,\,t)\Psi (x,\,t)$. The probability flux is defined as:

$\mathbf {j} ={\hbar \over m}\cdot {1 \over {2\mathrm {i} }}\left(\Psi ^{*}\nabla \Psi -\Psi \nabla \Psi ^{*}\right)={\hbar \over m}\operatorname {Im} \left(\Psi ^{*}\nabla \Psi \right)$

in units of (probability)/(area × time).

The probability flux satisfies the continuity equation:

${\partial \over \partial t}P\left(x,t\right)+\nabla \cdot \mathbf {j} =0$

where $P\left(x,t\right)$ is the probability density and measured in units of (probability)/(volume) = r⁻³. This equation is the mathematical equivalent of the probability conservation law.

For a plane wave:

$\Psi (x,t)=\,Ae^{\mathrm {i} (kx-\omega t)}$

$j\left(x,t\right)=\left|A\right|^{2}{\hbar k \over m}$

So that not only is the probability of finding the particle the same everywhere, but the probability flux is as expected from an object moving at the classical velocity $p/m$.

The reason that the Schrödinger equation admits a probability flux is because all the hopping is local and forward in time.

Heisenberg observables

There are many linear operators which act on the wavefunction, each one defines a Heisenberg matrix when the energy eigenstates are discrete. For a single particle, the operator which takes the derivative of the wavefunction in a certain direction:

${\hat {p}}=-{i\hbar {\partial \over \partial x}}$

Is called the momentum operator. Multiplying operators is just like multiplying matrices, the product of A and B acting on $\psi$ is A acting on the output of B acting on $\psi$.

An eigenstate of p obeys the equation:

${\hat {p}}\psi =k\psi \,$

for a number k, and for a normalizable wavefunction this restricts k to be real, and the momentum eigenstate is a wave with frequency k.

$\psi (x)=e^{ikx}\,$

The position operator x multiplies each value of the wavefunction at the position x by x:

${\hat {x}}(\psi )=x\psi$

So that in order to be an eigenstate of x, a wavefunction must be entirely concentrated at one point:

${\hat {x}}\delta (x-x_{0})=x_{0}\delta (x-x_{0})$

In terms of p, the Hamiltonian is:

${\hat {H}}={{\hat {p}}^{2} \over 2m}+V(x)$

It is easy to verify that p acting on x acting on psi:

${\hat {p}}({\hat {x}}(\psi ))=-i\hbar {\partial \over \partial x}(x\psi )=-i\hbar x{\partial \over \partial x}\psi -i\hbar \psi$

while x acting on p acting on psi reproduces only the first term:

${\hat {x}}({\hat {p}}(\psi ))=-i\hbar x{\partial \over \partial x}\psi$

so that the difference of the two is not zero:

$(xp-px)\psi =i\hbar \psi \,$

or in terms of operators:

$[x,p]=xp-px=i\hbar \,$

Since the time derivative of a state is:

$i\hbar {\partial \over \partial t}\Psi ={\hat {H}}\Psi \,$

while the complex conjugate is

$-i\hbar {\partial \over \partial t}\Psi ^{*}={\hat {H}}\Psi ^{*}\,$

The time derivative of a matrix element

${d \over dt}\langle \eta |{\hat {A}}|\Psi \rangle =-\langle \eta |{\hat {H}}{\hat {A}}|\Psi \rangle +\langle \eta |{\hat {A}}{\hat {H}}|\Psi \rangle =\langle \eta |[{\hat {H}},{\hat {A}}]|\Psi \rangle \,$

obeys the Heisenberg equation of motion. This establishes the equivalence of the Schrödinger and Heisenberg formalisms, ignoring the mathematical fine points of the limiting procedure for continuous space.

Correspondence principle

Ver artigo principal: Ehrenfest Theorem

The Schrödinger equation satisfies the correspondence principle. In the limit of small wavelength wavepackets, it reproduces Newton's laws. This is easy to see from the equivalence to matrix mechanics.

All operators in Heisenberg's formalism obey the quantum analog of Hamilton's equations:

${dA \over dt}=-i\hbar (AH-HA)$

So that in particular, the equations of motion for the X and P operators are:

${dX \over dt}={P \over m}$

${dP \over dt}=-{\partial V \over \partial x}$

in the Schrödinger picture, the interpretation of this equation is that it gives the time rate of change of the matrix element between two states when the states change with time. Taking the expectation value in any state shows that Newton's laws hold not only on average, but exactly, for the quantities:

$\langle X\rangle =\int _{x}\psi ^{*}(x)\psi (x)x=\langle \psi |X|\psi \rangle \,$

$\langle P\rangle =\int _{x}\psi ^{*}(x)i\hbar {\partial \psi \over \partial x}(x)=\langle \psi |P|\psi \rangle \,$

Relativity

Ver artigo principal: Relativistic wave equations

The Schrödinger equation does not take into account relativistic effects, as a wave equation, it is invariant under a Galilean transformation, but not under a Lorentz transformation. But in order to include relativity, the physical picture must be altered in a radical way.

The Klein–Gordon equation uses the relativistic mass-energy relation (in natural units):

$E^{2}=P^{2}+m^{2}\,$

to produce the differential equation:

$-{\partial ^{2} \over \partial t^{2}}\psi =-\nabla ^{2}\psi +m^{2}\psi \,$

which is relativistically invariant, but second order in $\psi$, and so cannot be an equation for the quantum state. This equation also has the property that there are solutions with both positive and negative frequency, a plane wave solution obeys:

$\omega ^{2}-k^{2}=m^{2}\,$

which has two solutions, one with positive frequency the other with negative frequency. This is a disaster for quantum mechanics, because it means that the energy is unbounded below.

A more sophisticated attempt to solve this problem uses a first order wave equation, the Dirac equation, but again there are negative energy solutions. In order to solve this problem, it is essential to go to a multiparticle picture, and to consider the wave equations as equations of motion for a quantum field, not for a wavefunction.

The reason is that relativity is incompatible with a single particle picture. A relativistic particle cannot be localized to a small region without the particle number becoming indefinite. When a particle is localized in a box of length L, the momentum is uncertain by an amount roughly proportional to h/L by the uncertainty principle. This leads to an energy uncertainty of hc/L, when |p| is large enough so that the mass of the particle can be neglected. This uncertainty in energy is equal to the mass-energy of the particle when

$L={\hbar \over mc}\,$

and this is called the Compton wavelength. Below this length, it is impossible to localize a particle and be sure that it stays a single particle, since the energy uncertainty is large enough to produce more particles from the vacuum by the same mechanism that localizes the original particle.

But there is another approach to relativistic quantum mechanics which does allow you to follow single particle paths, and it was discovered within the path-integral formulation. If the integration paths in the path integral include paths which move both backwards and forwards in time as a function of their own proper time, it is possible to construct a purely positive frequency wavefunction for a relativistic particle. This construction is appealing, because the equation of motion for the wavefunction is exactly the relativistic wave equation, but with a nonlocal constraint that separates the positive and negative frequency solutions. The positive frequency solutions travel forward in time, the negative frequency solutions travel backwards in time. In this way, they both analytically continue to a statistical field correlation function, which is also represented by a sum over paths. But in real space, they are the probability amplitudes for a particle to travel between two points, and can be used to generate the interaction of particles in a point-splitting and joining framework. The relativistic particle point of view is due to Richard Feynman.

Feynman's method also constructs the theory of quantized fields, but from a particle point of view. In this theory, the equations of motion for the field can be interpreted as the equations of motion for a wavefunction only with caution--- the wavefunction is only defined globally, and in some way related to the particle's proper time. The notion of a localized particle is also delicate--- a localized particle in the relativistic particle path integral corresponds to the state produced when a local field operator acts on the vacuum, and exacly which state is produced depends on the choice of field variables.

Solutions

Some general techniques are:

• Perturbation theory
• The variational principle
• Quantum Monte Carlo methods
• Density functional theory
• The WKB approximation and semi-classical expansion

In some special cases, special methods can be used:

• List of quantum mechanical systems with analytical solutions
• Hartree-Fock method and post Hartree-Fock methods
• Discrete delta-potential method

Free Schrödinger equation

When the potential is zero, the Schrödinger equation is linear with constant coefficients:

$i\hbar {\frac {\partial \Psi }{\partial t}}=-{\hbar ^{2} \over 2m}\nabla ^{2}\Psi$

The solution $\Psi (x,\,t)$ for any initial condition $\psi _{0}(x)$ can be found by Fourier transforms. Because the coefficients are constant, an initial plane wave stays a plane wave. Only the coefficient changes:

$\Psi (x,\,t)=A(t)e^{ikx}\,$

Substituting:

${dA(t) \over dt}=-{i\hbar k^{2} \over 2m}A(t)\,$

So that A is also oscillating in time:

$A(t)=Ae^{-i\hbar {k^{2} \over 2m}t}\,$

and the solution is:

$\Psi (x,\,t)=Ae^{ikx-i\omega t}\,$

Where $\omega =\hbar k^{2}/2m$, a restatement of DeBroglie's relations.

To find the general solution, write the initial condition as a sum of plane waves by taking its Fourier transform:

$\psi _{0}(x)=\int _{k}\psi (k)e^{ikx}\,$

The equation is linear, so each plane waves evolves independently:

$\Psi (x,\,t)=\int _{k}\psi (k)e^{-i\omega t}e^{ikx}\,$

Which is the general solution. When complemented by an effective method for taking Fourier transforms, it becomes an efficient algorithm for finding the wavefunction at any future time--- Fourier transform the initial conditions, multiply by a phase, and transform back.

Gaussian wavepacket

An easy and instructive example is the Gaussian wavepacket:

$\psi _{0}(x)=e^{-x^{2}/2a}\,$

where a is a positive real number, the square of the width of the wavepacket. The total normalization of this wavefunction is:

$\langle \psi |\psi \rangle =\int _{x}\psi ^{*}\psi ={\sqrt {\pi a}}$

The Fourier transform is a Gaussian again in terms of the wavenumber k:

$\psi _{0}(k)=(2\pi a)^{d/2}e^{-ak^{2}/2}\,$

With the physics convention which puts the factors of $2\pi$ in Fourier transforms in the k-measure.

$\psi _{0}(x)=\int _{k}\psi _{0}(k)e^{-ikx}=\int {d^{d}k \over (2\pi )^{d}}\psi _{0}(k)e^{-ikx}$

Each separate wave only phase-rotates in time, so that the time dependent Fourier-transformed solution is:

$\psi _{t}(k)=(2\pi a)^{d/2}e^{-a{k^{2} \over 2}-it{k^{2} \over 2m}}=(2\pi a)^{d/2}e^{-(a+it/m){k^{2} \over 2}}\,$

The inverse Fourier transform is still a Gaussian, but the parameter a has become complex, and there is an overall normalization factor.

$\psi _{t}(x)=\left({a \over a+it/m}\right)^{d/2}e^{-{x^{2} \over 2(a+it/m)}}\,$

The branch of the square root is determined by continuity in time--- it is the value which is nearest to the positive square root of a. It is convenient to rescale time to absorb m, replacing t/m by t.

The integral of $\psi$ over all space is invariant, because it is the inner product of $\psi$ with the state of zero energy, which is a wave with infinite wavelength, a constant function of space. For any energy state, with wavefunction $\eta (x)$, the inner product:

$\langle \eta |\psi \rangle =\int _{x}\eta (x)\psi _{t}(x)$,

only changes in time in a simple way: its phase rotates with a frequency determined by the energy of $\eta$. When $\eta$ has zero energy, like the infinite wavelength wave, it doesn't change at all.

The sum of the absolute square of $\psi$ is also invariant, which is a statement of the conservation of probability. Explicitly in one dimension:

$|\psi |^{2}=\psi \psi ^{*}={a \over {\sqrt {a^{2}+t^{2}}}}e^{-{x^{2}a \over a^{2}+t^{2}}}$

Which gives the norm:

$\int |\psi |^{2}={\sqrt {\pi a}}$

which has preserved its value, as it must.

The width of the Gaussian is the interesting quantity, and it can be read off from the form of $|\psi ^{2}|$:

${\sqrt {a^{2}+t^{2} \over a}}\,$.

The width eventually grows linearly in time, as $\scriptstyle t/{\sqrt {a}}$. This is wave-packet spreading--- no matter how narrow the initial wavefunction, a Schrödinger wave eventually fills all of space. The linear growth is a reflection of the momentum uncertainty--- the wavepacket is confined to a narrow width $\scriptstyle {\sqrt {a}}$ and so has a momentum which is uncertain by the reciprocal amount $\scriptstyle 1/{\sqrt {a}}$, a spread in velocity of $\scriptstyle 1/m{\sqrt {a}}$, and therefore in the future position by $\scriptstyle t/m{\sqrt {a}}$, where the factor of m has been restored by undoing the earlier rescaling of time.

Galilean invariance

Galilean boosts are transformations which look at the system from the point of view of an observer moving with a steady velocity -v. A boost must change the physical properties of a wavepacket in the same way as in classical mechanics:

$p'=p+mv\,$

$x'=x+vt\,$

So that the phase factor of a free Schrödinger plane wave:

$px-Et=(p'-mv)(x'-vt)-{(p'-mv)^{2} \over 2m}t=p'x'+E't+mvx-{mv^{2} \over 2}t\,$

is only different in the boosted coordinates by a phase which depends on x and t, but not on p.

An arbitrary superposition of plane wave solutions with different values of p is the same superposition of boosted plane waves, up to an overall x,t dependent phase factor. So any solution to the free Schrödinger equation, $\psi _{t}(x)$, can be boosted into other solutions:

$\psi '_{t}(x)=\psi _{t}(x+vt)e^{imvx-i{mv^{2} \over 2}t}\,$

Boosting a constant wavefunction produces a plane-wave. More generally, boosting a plane-wave:

$\psi _{t}(x)=e^{ipx-i{p^{2} \over 2m}t}\,$

produces a boosted wave:

$\psi '_{t}(x)=e^{ip(x+vt)-i{p^{2} \over 2m}t+imvx-i{mv^{2} \over 2}t}=e^{i(p+mv)x+i{(p+mv)^{2} \over 2m}t}\,$

Boosting the spreading Gaussian wavepacket:

$\psi _{t}(x)={1 \over {\sqrt {a+it/m}}}e^{-{x^{2} \over 2a}}\,$

produces the moving Gaussian:

$\psi _{t}(x)={1 \over {\sqrt {a+it/m}}}e^{-{(x+vt)^{2} \over 2a}+imvx-i{mv^{2} \over 2}t}\,$

Which spreads in the same way.

Free propagator

The narrow-width limit of the Gaussian wavepacket solution is the propagator K. For other differential equations, this is sometimes called the Green's function, but in quantum mechanics it is traditional to reserve the name Green's function for the time Fourier transform of K. When a is the infinitesimal quantity $\epsilon$, the Gaussian initial condition, rescaled so that its integral is one:

$\psi _{0}(x)={1 \over {\sqrt {2\pi \epsilon }}}e^{-{x^{2} \over 2\epsilon }}\,$

becomes a delta function, so that its time evolution:

$K_{t}(x)={1 \over {\sqrt {2\pi (it+\epsilon )}}}e^{-x^{2} \over 2it+\epsilon }\,$

gives the propagator.

Note that a very narrow initial wavepacket instantly becomes infinitely wide, with a phase which is more rapidly oscillatory at large values of x. This might seem strange--- the solution goes from being concentrated at one point to being everywhere at all later times, but it is a reflection of the momentum uncertainty of a localized particle. Also note that the norm of the wavefunction is infinite, but this is also correct since the square of a delta function is divergent in the same way.

The factor of $\epsilon$ is an infinitesimal quantity which is there to make sure that integrals over K are well defined. In the limit that $\epsilon$ becomes zero, K becomes purely oscillatory and integrals of K are not absolutely convergent. In the remainder of this section, it will be set to zero, but in order for all the integrations over intermediate states to be well defined, the limit $\scriptstyle \epsilon \rightarrow 0$ is to only to be taken after the final state is calculated.

The propagator is the amplitude for reaching point x at time t, when starting at the origin, x=0. By translation invariance, the amplitude for reaching a point x when starting at point y is the same function, only translated:

$K_{t}(x,y)=K_{t}(x-y)={1 \over {\sqrt {2\pi it}}}e^{-i(x-y)^{2} \over 2t}\,$

In the limit when t is small, the propagator converges to a delta function:

$\lim _{t\rightarrow 0}K_{t}(x-y)=\delta (x-y)$

but only in the sense of distributions. The integral of this quantity multiplied by an arbitrary differentiable test function gives the value of the test function at zero. To see this, note that the integral over all space of K is equal to 1 at all times:

$\int _{x}K_{t}(x)=1\,$

since this integral is the inner-product of K with the uniform wavefunction. But the phase factor in the exponent has a nonzero spatial derivative everywhere except at the origin, and so when the time is small there are fast phase cancellations at all but one point. This is rigorously true when the limit $\epsilon \rightarrow zero$ is taken after everything else.

So the propagation kernel is the future time evolution of a delta function, and it is continuous in a sense, it converges to the initial delta function at small times. If the initial wavefunction is an infinitely narrow spike at position $x_{0}$:

$\psi _{0}(x)=\delta (x-x_{0})\,$

it becomes the oscillatory wave:

$\psi _{t}(x)={1 \over {\sqrt {2\pi it}}}e^{-i(x-x_{0})^{2}/2t}\,$

Since every function can be written as a sum of narrow spikes:

$\psi _{0}(x)=\int _{y}\psi _{0}(y)\delta (x-y)\,$

the time evolution of every function is determined by the propagation kernel:

$\psi _{t}(x)=\int _{y}\psi _{0}(x){1 \over {\sqrt {2\pi it}}}e^{-i(x-x_{0})^{2}/2t}\,$

And this is an alternate way to express the general solution. The interpretation of this expression is that the amplitude for a particle to be found at point x at time t is the amplitude that it started at $x_{0}$ times the amplitude that it went from $x_{0}$ to x, summed over all the possible starting points. In other words, it is a convolution of the kernel K with the initial condition.

$\psi _{t}=K*\psi _{0}\,$

Since the amplitude to travel from x to y after a time $t+t'$ can be considered in two steps, the propagator obeys the identity:

$\int _{y}K(x-y;t)K(y-z;t')=K(x-z;t+t')\,$

Which can be interpreted as follows: the amplitude to travel from x to z in time t+t' is the sum of the amplitude to travel from x to y in time t multiplied by the amplitude to travel from y to z in time t', summed over all possible intermediate states y. This is a property of an arbitrary quantum system, and by subdividing the time into many segments, it allows the time evolution to be expressed as a path integral.

Analytic continuation to diffusion

The spreading of wavepackets in quantum mechanics is directly related to the spreading of probability densities in diffusion. For a particle which is random walking, the probability density function at any point satisfies the diffusion equation:

${\partial \over \partial t}\rho ={1 \over 2}{\partial \over \partial x^{2}}\rho$

where the factor of 2, which can be removed by a rescaling either time or space, is only for convenience.

A solution of this equation is the spreading gaussian:

$\rho _{t}(x)={1 \over {\sqrt {2\pi t}}}e^{-x^{2} \over 2t}$

and since the integral of $\rho _{t}$, is constant, while the width is becoming narrow at small times, this function approaches a delta function at t=0:

$\lim _{t\rightarrow 0}\rho _{t}(x)=\delta (x)\,$

again, only in the sense of distributions, so that

$\lim _{t\rightarrow 0}\int _{x}f(x)\rho _{t}(x)=f(0)\,$

for any smooth test function f.

The spreading Gaussian is the propagation kernel for the diffusion equation and it obeys the convolution identity:

$K_{t+t'}=K_{t}*K_{t'}\,$

Which allows diffusion to be expressed as a path integral. The propagator is the exponential of an operator H:

$K_{t}(x)=e^{-tH}\,$

which is the infinitesimal diffusion operator.

$H=-{\nabla ^{2} \over 2}\,$

A matrix has two indices, which in continuous space makes it a function of x and x'. In this case, because of translation invariance, the matrix element K only depend on the difference of the position, and a convenient abuse of notation is to refer to the operator, the matrix elements, and the function of the difference by the same name:

$K_{t}(x,x')=K_{t}(x-x')\,$

Translation invariance means that continuous matrix multiplication:

$C(x,x'')=\int _{x'}A(x,x')B(x',x'')\,$

is really convolution:

$C(\Delta )=C(x-x'')=\int _{x'}A(x-x')B(x'-x'')=\int _{y}A(\Delta -y)B(y)\,$

The exponential can be defined over a range of t's which include complex values, so long as integrals over the propagation kernel stay convergent.

$K_{z}(x)=e^{-zH}\,$

As long as the real part of z is positive, for large values of x K is exponentially decreasing and integrals over K are absolutely convergent.

The limit of this expression for z coming close to the pure imaginary axis is the Schrödinger propagator:

$K_{t}^{\rm {Schr}}=K_{it+\epsilon }=e^{-(it+\epsilon )H}\,$

and this gives a more conceptual explanation for the time evolution of Gaussians. From the fundamental identity of exponentiation, or path integration:

$K_{z}*K_{z'}=K_{z+z'}\,$

holds for all complex z values where the integrals are absolutely convergent so that the operators are well defined.

So that quantum evolution starting from a Gaussian, which is the diffusion kernel K:

$\psi _{0}(x)=K_{a}(x)=K_{a}*\delta (x)\,$

gives the time evolved state:

$\psi _{t}=K_{it}*K_{a}=K_{a+it}.\,$

This explains the diffusive form of the Gaussian solutions:

$\psi _{t}(x)={1 \over {\sqrt {2\pi (a+it)}}}e^{-{x^{2} \over 2(a+it)}}.\,$

Variational principle

The variational principle asserts that for any Hermitian matrix A, the eigenvector corresponding to the lowest eigenvalue minimizes the quantity:

$\langle v,Av\rangle =\sum _{ij}A_{ij}v_{i}^{*}v_{j}\,$

on the unit sphere $<v,v>=1$. This follows by the method of Lagrange multipliers, at the minimum the gradient of the function is parallel to the gradient of the constraint:

${\partial \over \partial v_{i}}\langle v,Av\rangle =\lambda {\partial \over \partial v_{i}}\langle v,v\rangle \,$

which is the eigenvalue condition

$\sum _{j}A_{ij}v_{j}=\lambda v_{i}\,$

so that the extreme values of a quadratic form A are the eigenvalues of A, and the value of the function at the extreme values is just the corresponding eigenvalue:

$\langle v,Av\rangle =\lambda \langle v,v\rangle =\lambda .\,$

When the hermitian matrix is the Hamiltonian, the minimum value is the lowest energy level.

In the space of all wavefunctions, the unit sphere is the space of all normalized wavefunctions $\psi$, the ground state minimizes

$\langle \psi |H|\psi \rangle =\int \psi ^{*}H\psi =\int \psi ^{*}(-\nabla ^{2}+V(x))\psi \,$

or, after an integration by parts,

$\langle \psi |H|\psi \rangle =\int |\nabla \psi |^{2}+V(x)|\psi |^{2}.\,$

All the stationary points come in complex conjugate pairs since the integrand is real. Since the stationary points are eigenvalues, any linear combination is a stationary point, and the real and imaginary part are both stationary points.

Potential and ground state

For a particle in a positive definite potential, the ground state wavefunction is real and positive, and has a dual interpretation as the probability density for a diffusion process. The analogy between diffusion and nonrelativistic quantum motion, originally discovered and exploited by Schrödinger, has led to many exact solutions.

A positive definite wavefunction:

$\psi =e^{-W(x)}\,$

is a solution to the time-independent Schrödinger equation with m=1 and potential:

$V(x)={1 \over 2}|\nabla W|^{2}-{1 \over 2}\nabla ^{2}W\,$

with zero total energy. W, the logarithm of the ground state wavefunction. The second derivative term is higher order in $\scriptstyle \hbar$, and ignoring it gives the semi-classical approximation.

The form of the ground state wavefunction is motivated by the observation that the ground state wavefunction is the Boltzmann probability for a different problem, the probability for finding a particle diffusing in space with the free-energy at different points given by W. If the diffusion obeys detailed balance and the diffusion constant is everywhere the same, the Fokker Planck equation for this diffusion is the Schrödinger equation when the time parameter is allowed to be imaginary. This analytic continuation gives the eigenstates a dual interpretation--- either as the energy levels of a quantum system, or the relaxation times for a stochastic equation.

Harmonic oscillator

Ver artigo principal: Quantum harmonic oscillator

W should grow at infinity, so that the wavefunction has a finite integral. The simplest analytic form is:

$W(x)=\omega x^{2}\,$

with an arbitrary constant $\omega$, which gives the potential:

$V(x)={1 \over 2}\omega ^{2}x^{2}-{\omega \over 2}\,$

This potential describes a Harmonic oscillator, with the ground state wavefunction:

$\psi (x)=e^{-\omega x^{2}}\,$

The total energy is zero, but the potential is shifted by a constant. The ground state energy of the usual unshifted Harmonic oscillator potential:

$V(x)={\omega x^{2} \over 2}\,$

is then the additive constant:

$E_{0}={a \over 2}\,$

which is the zero point energy of the oscillator.

Coulomb potential

Another simple but useful form is

$W(x)=2a|x|\,$

where W is proportional to the radial coordinate. This is the ground state for two different potentials, depending on the dimension. In one dimension, the corresponding potential is singular at the origin, where it has some nonzero density:

$V(x)=2a^{2}+a\delta (x)\,$

and, up to some rescaling of variables, this is the lowest energy state for a delta function potential, with the bound state energy added on.

$V(x)=a\delta (x)\,$

with the ground state energy:

$E_{0}=-2a^{2}\,$

and the ground state wavefunction:

$\psi =e^{-2a|x|}\,$

In higher dimensions, the same form gives the potential:

$V(x)=2a^{2}+{2a(d-1) \over r};\,$

which can be identified as the attractive Coulomb law, up to an additive constant which is the ground state energy. This is the superpotential that describes the lowest energy level of the Hydrogen atom, once the mass is restored by dimensional analysis:

$\psi _{0}=e^{-r/r_{0}}\,$

where $r_{0}$ is the Bohr radius, with energy

$E_{0}=-{2a \over d-1}\,$

The ansatz

$W(x)=ar+b\log(r)\,$

modifies the Coulomb potential to include a quadratic term proportional to $1/r^{2}$, which is useful for nonzero angular momentum.

Operator formalism

Bra-ket notation

Ver artigo principal: Bra-ket notation

In the mathematical formulation of quantum mechanics, a physical system is fully described by a vector in a complex Hilbert space, the collection of all possible normalizable wavefunctions. The wavefunction is just an alternate name for the vector of complex amplitudes, and only in the case of a single particle in the position representation is it a wave in the usual sense, a wave in space time. For more complex systems, it is a wave in an enormous space of all possible worlds. Two nonzero vectors which are multiples of each other, two wavefunctions which are the same up to rescaling, represent the same physical state.

The wavefunction vector can be written in several ways:

1. as an abstract ket vector:

$|\psi \rangle$

2. As a list of complex numbers, the components relative to a discrete list of normalizable basis vectors $|\eta _{i}\rangle$:

$c_{i}=\langle \eta _{i}|\psi \rangle$

3. As a continuous superposition of non-normalizable basis vectors, like position states $|x\rangle$:

$|\psi \rangle =\int _{x}\psi (x)|xdx\rangle$

The divide between the continuous basis and the discrete basis can be bridged by limiting arguments. The two can be formally unified by thinking of each as a measure on the real number line.

In the most abstract notation, the Schrödinger equation is written:

$i\hbar {d \over dt}|\psi \rangle =H|\psi \rangle$

which only says that the wavefunction evolves linearly in time, and names the linear operator which gives the time derivative the Hamiltonian H. In terms of the discrete list of coefficients:

$i\hbar {d \over dt}C_{i}=\sum _{j}H_{ij}C_{j}$

which just reaffirms that time evolution is linear, since the Hamiltonian acts by matrix multiplication.

In a continuous representation, the Hamiltonian is a linear operator, which acts by the continuous version of matrix multiplication:

$\langle x|i\hbar {d \over dt}|\psi \rangle =\langle x|H|\psi \rangle ={\hat {H}}\psi (x)$

Taking the complex conjugate:

$-i\hbar {d \over dt}\langle \psi |=\langle \psi |H^{\dagger }$

In order for the time-evolution to be unitary, to preserve the inner products, the time derivative of the inner product must be zero:

$i\hbar {d \over dt}\langle \psi |\psi \rangle =\langle \psi |H|\psi \rangle -\langle \psi |H^{\dagger }|\psi \rangle =0$

for an arbitrary state $|\psi \rangle$, which requires that H is Hermitian. In a discrete representation this means that $\scriptstyle H_{ij}=H_{ji}$. When H is continuous, it should be self-adjoint, which adds some technical requirement that H does not mix up normalizable states with states which violate boundary conditions or which are grossly unnormalizable.

The formal solution of the equation is the matrix exponential (natural units):

$|\psi (t)\rangle =e^{-iHt}|\psi (0)\rangle =U(t)|\psi (0)\rangle$

For every time-independent Hamiltonian operator, ${\hat {H}}$, there exists a set of quantum states, $\left|\psi _{n}\right\rangle$, known as energy eigenstates, and corresponding real numbers $E_{n}$ satisfying the eigenvalue equation.

$H|\psi _{n}\rangle =E_{n}|\psi _{n}\rangle \,$

This is the time-independent Schrödinger equation.

For the case of a single particle, the Hamiltonian is the following linear operator (natural units):

$H=-{\nabla ^{2} \over 2m}+V(x)={p^{2} \over 2m}+V(x)$

which is a Self-adjoint operator when V is not too singular and does not grow too fast. Self-adjoint operators have the property that their eigenvalues are real in any basis, and their eigenvectors form a complete set, either discrete or continuous.

Expressed in a basis of Eigenvectors of H, the Schrödinger equation becomes trivial:

$\mathrm {i} \hbar {\frac {\partial }{\partial t}}\left|\psi _{n}\left(t\right)\right\rangle =E_{n}\left|\psi _{n}\left(t\right)\right\rangle .$

Which means that each energy eigenstate is only multiplied by a complex phase:

$\left|\psi \left(t\right)\right\rangle =\mathrm {e} ^{-\mathrm {i} Et/\hbar }\left|\psi \left(0\right)\right\rangle .$

Which is what matrix exponentiation means--- the time evolution acts to rotate the eigenfunctions of H.

When H is expressed as a matrix for wavefunctions in a discrete energy basis:

$i\hbar {d \over dt}C_{i}=E_{i}C_{i}\,$

so that:

$C_{n}(t)=e^{-iE_{n}t}C_{n}(0)\,$

The physical properties of the C's are extracted by acting by operators, matrices. By redefining the basis so that it rotates with time, the matrices become time dependent, which is the Heisenberg picture.

Galilean invariance

Galilean symmetry requires that H(p) is quadratic in p in both the classical and quantum Hamiltonian formalism. In order for Galilean boosts to produce a p-independent phase factor, px - Ht must have a very special form--- translations in p need to be compensated by a shift in H. This is only true when H is quadratic.

The infinitesimal generator of Boosts in both the classical and quantum case is:

$B=\sum _{i}m_{i}x_{i}(t)-t\sum _{i}p_{i}\,$

where the sum is over the different particles, and B,x,p are vectors.

The poisson bracket/commutator of $\scriptstyle B\cdot v$ with x and p generate infinitesimal boosts, with v the infinitesimal boost velocity vector:

$[B\cdot v,x_{i}]=vt\,$

$[B\cdot v,p_{i}]=vm_{i}\,$

Iterating these relations is simple, since they add a constant amount at each step. By iterating, the dv's incrementally sum up to the finite quantity V:

$x\rightarrow x_{i}+Vt\,$

$p\rightarrow p_{i}+m_{i}V\,$

B divided by the total mass is the current center of mass position minus the time times the center of mass velocity:

$B=MX_{\mathrm {cm} }-tP_{\mathrm {cm} }\,$

In other words, B/M is the current guess for the position that the center of mass had at time zero.

The statement that B doesn't change with time is the center of mass theorem. For a Galilean invariant system, the center of mass moves with a constant velocity, and the total kinetic energy is the sum of the center of mass kinetic energy and the kinetic energy measured relative to the center of mass.

Since B is explicitly time dependent, H does not commute with B, rather:

${dB \over dt}=[H,B]+{\partial B \over \partial t}=0\,$

this gives the transformation law for H under infinitesimal boosts:

$[B\cdot v,H]=-P_{\mathrm {cm} }v\,$

the interpretation of this formula is that the change in H under an infinitesimal boost is entirely given by the change of the center of mass kinetic energy, which is the dot product of the total momentum with the infinitesimal boost velocity.

The two quantities (H,P) form a representation of the Galilean group with central charge M, where only H and P are classical functions on phase-space or quantum mechanical operators, while M is a parameter. The transformation law for infinitesimal v:

$P'=P+Mv\,$

$H'=H-P{\dot {v}}\,$

can be iterated as before--- P goes from P to P+MV in infinitesimal increments of v, while H changes at each step by an amount proportional to P, which changes linearly. The final value of H is then changed by the value of P halfway between the starting value and the ending value:

$H'=H-(P+{MV \over 2})\cdot V=H-P\cdot V-{MV^{2} \over 2}.\,$

The factors proportional to the central charge M are the extra wavefunction phases.

Boosts give too much information in the single-particle case, since Galilean symmetry completely determines the motion of a single particle. Given a multi-particle time dependent solution:

$\psi _{t}(x_{1},x_{2}...,x_{n})\,$

with a potential that depends only on the relative positions of the particles, it can be used to generate the boosted solution:

$\psi '_{t}=\psi _{t}(x_{1}+vt,...,x_{2}+vt)e^{iP_{\mathrm {cm} }\cdot X_{\mathrm {cm} }-{Mv_{\mathrm {cm} }^{2} \over 2}t}.\,$

For the standing wave problem, the motion of the center of mass just adds an overall phase. When solving for the energy levels of multiparticle systems, Galilean invariance allows the center of mass motion to be ignored.

See also

• Dirac equation
• Quantum number
• Relation between Schrödinger's equation and the path integral formulation of quantum mechanics
• Schrödinger's cat
• Schrödinger field
• Schrödinger picture
• Theoretical and experimental justification for the Schrödinger equation

Notes

References

• Paul Adrien Maurice Dirac (1958). The Principles of Quantum Mechanics 4th ed. [S.l.]: Oxford University Press 

• David J. Griffiths (2004). Introduction to Quantum Mechanics 2nd ed. [S.l.]: Benjamin Cummings 

• Richard Liboff (2002). Introductory Quantum Mechanics 4th ed. [S.l.]: Addision Wesley 

• David Halliday (2007). Fundamentals of Physics 8th ed. [S.l.]: Wiley 

• Serway, Moses, and Moyer (2004). Modern Physics 3rd ed. [S.l.]: Brooks Cole  !CS1 manut: Nomes múltiplos: lista de autores (link)

• Walter John Moore (1992). Schrödinger: Life and Thought. [S.l.]: Cambridge University Press 

• Schrödinger, Erwin (1926). «An Undulatory Theory of the Mechanics of Atoms and Molecules». Phys. Rev. 28 (6). 28: 1049–1070. doi:10.1103/PhysRev.28.1049 

External links

• Quantum Physics - a textbook with a treatment of the time-independent Schrödinger equation
• Linear Schrödinger Equation at EqWorld: The World of Mathematical Equations.
• Nonlinear Schrödinger Equation at EqWorld: The World of Mathematical Equations.
• The Schrödinger Equation in One Dimension as well as the directory of the book.
• All about 3D Schrödinger Equation

• Mathematical aspects of Schrödinger equation's are discussed on the Dispersive PDE Wiki.
• Web-Schrödinger: Interactive solution of the 2D time dependent Schrödinger equation

Category:Fundamental physics concepts Category:Partial differential equations Category:Quantum mechanics Category:Equations Category:Austrian inventions pt:Equação de Schrödinger

A wave function or wavefunction is a mathematical tool used in quantum mechanics to describe any physical system. It is a function from a space that maps the possible states of the system into the complex numbers. The laws of quantum mechanics (i.e. the Schrödinger equation) describe how the wave function evolves over time. The values of the wave function are probability amplitudes — complex numbers — the squares of the absolute values of which give the probability distribution that the system will be in any of the possible states.

The electron probability density for the first few hydrogen atom electron orbitals shown as cross-sections. These orbitals form an orthonormal basis for the wave function of the electron.

Predefinição:Quantum mechanics It is commonly applied as a property of particles relating to their wave-particle duality, where it is denoted $\psi (position,time)$ and where $|\psi |^{2}$ is equal to the chance of finding the subject at a certain time and position. For example, in an atom with a single electron, such as hydrogen or ionized helium, the wave function of the electron provides a complete description of how the electron behaves. It can be decomposed into a series of atomic orbitals which form a basis for the possible wave functions. For atoms with more than one electron (or any system with multiple particles), the underlying space is the possible configurations of all the electrons and the wave function describes the probabilities of those configurations.

Definition

The modern usage of the term wave function refers to a complex vector or function, i.e. an element in a complex Hilbert space. Typically, a wave function is either:

• a complex vector with finitely many components

${\vec {\psi }}={\begin{bmatrix}c_{1}\\\vdots \\c_{n}\end{bmatrix}}$,

• a complex vector with infinitely many components

${\vec {\psi }}={\begin{bmatrix}c_{1}\\\vdots \\c_{n}\\\vdots \end{bmatrix}}$,

• a complex function of one or more real variables (a continuously indexed complex vector)

$\psi (x_{1},\,\ldots \,x_{n})$.

In all cases, the wave function provides a complete description of the associated physical system. An element of a vector space can be expressed in different bases; and so the same applies to wave functions. The components of a wave function describing the same physical state take different complex values depending on the basis being used; however the wave function itself is not dependent on the basis chosen; in this respect they are like spatial vectors in ordinary space: choosing a new set of cartesian axes by rotation of the coordinate frame does not alter the vector itself, only the representation of the vector with respect to the coordinate frame. A basis in quantum mechanics is analogous to the coordinate frame: choosing a new basis does not alter the wavefunction, only its representation, which is expressed as the values of the components above.

Because the probabilities that the system is in each possible state should add up to 1, the norm of the wave function must be 1.

Spatial interpretation

The physical interpretation of the wave function is context dependent. Several examples are provided below, followed by a detailed discussion of the three cases described above.

One particle in one spatial dimension

The spatial wavefunction has no actual value and is impossible to solve.

The spatial wave function associated with a particle in one dimension is a complex function $\psi (x)\,$ defined over the real line. The positive function $|\psi |^{2}\,$ is interpreted as the probability density associated with the particle's position. That is, the probability of a measurement of the particle's position yielding a value in the interval $[a,b]$ is given by

$\mathbf {P} _{ab}=\int _{a}^{b}|\psi (x)|^{2}\,dx$.

This leads to the normalization condition

$\int _{-\infty }^{\infty }|\psi (x)|^{2}\,dx=1\quad$.

since the probability of a measurement of the particle's position yielding a value in the range $(-\infty ,\infty )$ is unity.

One particle in three spatial dimensions

The three dimensional case is analogous to the one dimensional case; the wave function is a complex function $\psi (x,y,z)\,$ defined over three dimensional space, and the square of its absolute value is interpreted as a three dimensional probability density function:

$\mathbf {P} _{R}=\int _{R}|\psi (x,y,z)|^{2}\,dV$

The normalization condition is likewise

$\int _{R}|\psi (x,y,z)|^{2}\,dV=1$

where the preceding integral is taken over all space.

Two distinguishable particles in three spatial dimensions

In this case, the wave function is a complex function of six spatial variables, $\psi (x_{1},y_{1},z_{1},x_{2},y_{2},z_{2})\$, and $|\psi |^{2}\,$ is the joint probability density associated with the positions of both particles. Thus the probability that a measurement of the positions of both particles indicates particle one is in region $R$ and particle two is in region $S$ is

$\mathbf {P} _{R,S}=\int _{R}\int _{S}|\psi |^{2}\,dV_{2}\,dV_{1}$

where $dV_{1}=dx_{1}dy_{1}dz_{1}$, and similarly for $dV_{2}$.

The normalization condition is then:

$\int \int |\psi (x_{1},y_{1},z_{1},x_{2},y_{2},z_{2})|^{2}\,dV_{2}\,dV_{1}=1$

in which the preceding integral is taken over the full range of all six variables.

Given a wave function ψ of a system consisting of two (or more) particles, it is in general not possible to assign a definite wave function to a single-particle subsystem. In other words, the particles in the system can be entangled.

One particle in one dimensional momentum space

The wave function for a one dimensional particle in momentum space is a complex function $\psi (p)\,$ defined over the real line. The quantity $|\psi |^{2}\,$ is interpreted as a probability density function in momentum space:

$\mathbf {P} _{ab}=\int _{a}^{b}|\psi (p)|^{2}\,dp$

As in the position space case, this leads to the normalization condition:

$\int _{-\infty }^{\infty }|\psi (p)|^{2}\,dp=1.$

Spin 1/2

The wave function for a spin-½ particle (ignoring its spatial degrees of freedom) is a column vector

${\vec {\psi }}={\begin{bmatrix}c_{1}\\c_{2}\end{bmatrix}}$.

The meaning of the vector's components depends on the basis, but typically $c_{1}$ and $c_{2}$ are respectively the coefficients of spin up and spin down in the $z$ direction. In Dirac notation this is:

$|\psi \rangle =c_{1}|\uparrow _{z}\rangle +c_{2}|\downarrow _{z}\rangle$

The values $|c_{1}|^{2}\,$ and $|c_{2}|^{2}\,$ are then respectively interpreted as the probability of obtaining spin up or spin down in the z direction when a measurement of the particle's spin is performed. This leads to the normalization condition

$|c_{1}|^{2}+|c_{2}|^{2}=1\,$.

Interpretation

A wave function describes the state of a physical system, $|\psi \rangle \,$, by expanding it in terms of other possible states of the same system, $|\phi _{i}\rangle$. Collectively the latter are referred to as a basis or representation. In what follows, all wave functions are assumed to be normalized.

Finite dimensional basis vectors

A wave function which is a vector ${\vec {\psi }}$ with $n$ components describes how to express the state of the physical system $|\psi \rangle$ as the linear combination of finitely many basis elements $|\phi _{i}\rangle$, where $i$ runs from $1$ to $n$. In particular the equation

${\vec {\psi }}={\begin{bmatrix}c_{1}\\\vdots \\c_{n}\end{bmatrix}}$,

which is a relation between column vectors, is equivalent to

$|\psi \rangle =\sum _{i=1}^{n}c_{i}|\phi _{i}\rangle$,

which is a relation between the states of a physical system. Note that to pass between these expressions one must know the basis in use, and hence, two column vectors with the same components can represent two different states of a system if their associated basis states are different. An example of a wave function which is a finite vector is furnished by the spin state of a spin-1/2 particle, as described above.

The physical meaning of the components of ${\vec {\psi }}$ is given by the wave function collapse postulate:

If the states $|\phi _{i}\rangle$ have distinct, definite values, $\lambda _{i}$, of some dynamical variable (e.g. momentum, position, etc) and a measurement of that variable is performed on a system in the state

$|\psi \rangle =\sum _{i}c_{i}|\phi _{i}\rangle$

then the probability of measuring $\lambda _{i}$ is $|c_{i}|^{2}$, and if the measurement yields $\lambda _{i}$, the system is left in the state $|\phi _{i}\rangle$.

Infinite dimensional basis vectors

The case of an infinite vector with a discrete index is treated in the same manner a finite vector, except the sum is extended over all the basis elements. Hence

${\vec {\psi }}={\begin{bmatrix}c_{1}\\\vdots \\c_{n}\\\vdots \end{bmatrix}}$

is equivalent to

$|\psi \rangle =\sum _{i}c_{i}|\psi _{i}\rangle$,

where it is understood that the above sum includes all the components of ${\vec {\psi }}$. The interpretation of the components is the same as the finite case (apply the collapse postulate).

Continuously indexed vectors (functions)

In the case of a continuous index, the sum is replaced by an integral; an example of this is the spatial wave function of a particle in one dimension, which expands the physical state of the particle, $|\psi \rangle$, in terms of states with definite position, $|x\rangle$. Thus

$|\psi \rangle =\int _{-\infty }^{\infty }\psi (x)|x\rangle \,dx$.

Note that $|\psi \rangle$ is not the same as $\psi (x)\,$. The former is the actual state of the particle, whereas the latter is simply a wave function describing how to express the former as a superposition of states with definite position. In this case the base states themselves can be expressed as

$|x_{0}\rangle =\int _{-\infty }^{\infty }\delta (x-x_{0})|x\rangle \,dx$

and hence the spatial wave function associated with $|x_{0}\rangle$ is $\delta (x-x_{0})\,$ (where $\delta (x-x_{0})\,$ is the Dirac delta function).

Formalism

Given an isolated physical system, the allowed states of this system (i.e. the states the system could occupy without violating the laws of physics) are part of a Hilbert space $H$. Some properties of such a space are

1. If $|\psi \rangle$ and $|\phi \rangle$ are two allowed states, then

$a|\psi \rangle +b|\phi \rangle$

is also an allowed state, provided $|a|^{2}+|b|^{2}=1$. (This condition is due to normalisation.)

2. There is always an orthonormal basis of allowed states of the vector space H.

The wave function associated with a particular state may be seen as an expansion of the state in a basis of $H$. For example,

$\{|\uparrow _{z}\rangle ,|\downarrow _{z}\rangle \}$

is a basis for the space associated with the spin of a spin-1/2 particle and consequently the spin state of any such particle can be written uniquely as

$a|\uparrow _{z}\rangle +b|\downarrow _{z}\rangle$.

Sometimes it is useful to expand the state of a physical system in terms of states which are not allowed, and hence, not in $H$. An example of this is the spacial wave function associated with a particle in one dimension which expands the state of the particle in terms of states with definite position.

Every Hilbert space $H$ is equipped with an inner product. Physically, the nature of the inner product is contingent upon the kind of basis in use. When the basis is a countable set $\{|\phi _{i}\rangle \}\,$, and orthonormal, i.e.

$\langle \phi _{i}|\phi _{j}\rangle =\delta _{ij}.$

Then an arbitrary vector $|\psi \rangle$ can be expressed as

$|\psi \rangle =\sum _{i}c_{i}|\phi _{i}\rangle$

where $c_{i}=\langle \phi _{i}|\psi \rangle .$

If one chooses a "continuous" basis as, for example, the position or coordinate basis consisting of all states of definite position $\{|x\rangle \}$, the orthonormality condition holds similarly:

$\langle x|x'\rangle =\delta (x-x').$

We have the analogous identity

$\langle x|\int \psi (x')|x'\rangle \,dx'=\int \psi (x')\delta (x-x')\,dx'=\psi (x).$

Ontology

Whether the wave function is real, and what it represents, are major questions in the interpretation of quantum mechanics. Many famous physicists have puzzled over this problem, such as Erwin Schrödinger, Albert Einstein and Niels Bohr. Some approaches regard it as merely representing information in the mind of the observer. Some, ranging from Schrödinger, Einstein, David Bohm and Hugh Everett III and others, argued that the wavefunction must have an objective existence.

See also

• Boson
• Fermion
• Normalisable wave function
• Particle in a box
• Schrödinger equation
• Wave function collapse
• Wave packet

References

Further reading

• Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). [S.l.]: Prentice Hall. ISBN 0-13-111892-7 

Category:Quantum mechanics Category:Fundamental physics concepts pt:Função de onda

In quantum mechanics, wave function collapse (also called collapse of the state vector or reduction of the wave packet) is the process by which a wave function, initially in a superposition of different eigenstates, appears to reduce to a single one of the states after interaction with the external world. It is one of two processes by which quantum systems evolve in time according to the laws of quantum mechanics as presented by John von Neumann. The reality of wave function collapse has always been debated, i.e., whether it is a fundamental physical phenomenon in its own right or just an epiphenomenon of another process, such as quantum decoherence. In recent decades the quantum decoherence view has gained popularity.

Mathematical terminology

Predefinição:For The state, or wave function, of a physical system at some time can be expressed in Dirac or bra-ket notation as:

$|\psi \rangle =\sum _{i}|i\rangle \psi _{i}$

where the $\scriptstyle |i\rangle$s specify the different quantum "alternatives" available (technically, they form an orthonormal eigenvector basis, which implies $\scriptstyle \langle i|j\rangle =\delta _{ij}$). An observable or measurable parameter of the system is associated with each eigenbasis, with each quantum alternative having a specific value or eigenvalue, e_i, of the observable.

The $\scriptstyle \psi _{i}=\langle i|\psi \rangle$ are the probability amplitude coefficients, which are complex numbers. For simplicity we shall assume that our wave function is normalised: $\scriptstyle \langle \psi |\psi \rangle$, which implies that

$\langle \psi |\psi \rangle =\sum _{i}|\psi _{i}|^{2}=1.$

With these definitions it is easy to describe the process of collapse: when an external agency measures the observable associated with the eigenbasis then the state of the wave function changes from $\scriptstyle |\psi \rangle$ to just one of the $\scriptstyle |i\rangle$s with Born probability $\scriptstyle |\psi _{i}|^{2}$, that is:

$|\psi \rangle \Rightarrow |i\rangle$.

This is called collapse because all the other terms in the expansion of the wave function have vanished or collapsed into nothing. If a more general measurement is made that detects the system in a state $\scriptstyle |\phi \rangle$ then the system makes a "jump" or quantum leap from the original state $\scriptstyle |\psi \rangle$ to the final state $\scriptstyle |\phi \rangle$ with probability of $\scriptstyle |\langle \psi |\phi \rangle |^{2}$. Quantum leaps and wave function collapse are therefore opposite sides of the same coin.

History and context

By the time John von Neumann wrote his treatise Mathematische Grundlagen der Quantenmechanik in 1932, the phenomenon of "wave function collapse" was accommodated into the mathematical formulation of quantum mechanics by postulating that there were two processes of wave function change:

1. The probabilistic, non-unitary, non-local, discontinuous change brought about by observation and measurement, as outlined above.
2. The deterministic, unitary, continuous time evolution of an isolated system that obeys Schrödinger's equation (or nowadays some relativistic, local equivalent).

In general, quantum systems exist in superpositions of those basis states that most closely correspond to classical descriptions, and -- when not being measured or observed, evolve according to the time dependent Schrödinger equation, relativistic quantum field theory or some form of quantum gravity or string theory, which is process (2) mentioned above. However, when the wave function collapses -- process (1) -- from an observer's perspective the state seems to "leap" or "jump" to just one of the basis states and uniquely acquire the value of the property being measured, $e_{i}$, that is associated with that particular basis state. After the collapse, the system begins to evolve again according to the Schrödinger equation or some equivalent wave equation.

By explicitly dealing with the interaction of object and measuring instrument von Neumann^[1] has attempted to prove consistency of the two processes (1) and (2) of wave function change.

He was able to prove the possibility of a quantum mechanical measurement scheme consistent with wave function collapse. However, he did not prove necessity of such a collapse. Although von Neumann's projection postulate is often presented as a normative description of quantum measurement it should be realized that it was conceived by taking into account experimental evidence available during the 1930s (in particular the Compton-Simon experiment has been paradigmatic), and that many important present-day measurement procedures do not satisfy it (socalled measurements of the second kind).

The existence of the wave function collapse is required in

• the Copenhagen interpretation
• the objective collapse interpretations
• the so-called transactional interpretation
• in a "spiritual interpretation" in which consciousness causes collapse.

On the other hand, the collapse is considered as redundant or just an optional approximation in

• interpretations based on consistent histories
• the many-worlds interpretation
• the Bohm interpretation
• the Ensemble Interpretation

The cluster of phenomena described by the expression wave function collapse is a fundamental problem in the interpretation of quantum mechanics known as the measurement problem. The problem is not really confronted by the Copenhagen interpretation which simply postulates that this is a special characteristic of the "measurement" process. The Everett many-worlds interpretation deals with it by discarding the collapse-process, thus reformulating the relation between measurement apparatus and system in such a way that the linear laws of quantum mechanics are universally valid, that is, the only process according to which a quantum system evolves is governed by the Schrödinger equation or some relativistic equivalent. Often tied in with the many-worlds interpretation, but not limited to it, is the physical process of decoherence, which causes an apparent collapse. Decoherence is also important for the interpretation based on Consistent Histories.

Note that a general description of the evolution of quantum mechanical systems is possible by using density operators and quantum operations. In this formalism (which is closely related to the C*-algebraic formalism) the collapse of the wave function corresponds to a non-unitary quantum operation.

Note also that the physical significance ascribed to the wave function varies from interpretation to interpretation, and even within an interpretation, such as the Copenhagen Interpretation. If the wave function merely encodes an observer's knowledge of the universe then the wave function collapse corresponds to the receipt of new information -- this is somewhat analogous to the situation in classical physics, except that the classical "wave function" does not necessarily obey a wave equation. If the wave function is physically real, in some sense and to some extent, then the collapse of the wave function is also seen as a real process, to the same extent. One of the paradoxes of quantum theory is that wave function seems to be more than just information (otherwise interference effects are hard to explain) and often less than real, since the collapse seems to take place faster-than-light and triggered by observers.

Notes

See also

• Arrow of time
• Interpretation of quantum mechanics
• Quantum decoherence
• Quantum interference
• Schrödinger's cat
• Zeno effect

Category:Quantum measurement Category:Fundamental physics concepts pt:Colapso da função de onda