Usuário:Amom Lins/Rascunhos/Polígono de Newton

Na matemática, o polígono de Newton é uma ferramenta para entender o comportamento dos polinômios sobre corpos locais .
No caso original, o campo de interesse local era o campo da série de Laurent para um X indeterminado, ou seja, o campo de frações da série de potências anelares.
- K [[X]],
sobre K, onde K era o número real ou o campo numérico complexo . Isso ainda é de utilidade considerável em relação às expansões de Puiseux . O polígono de Newton é um dispositivo eficaz para entender os termos principais
- aX r
das soluções de expansão de séries de potência para equações
- P(F(X)) = 0
onde P é um polinômio com coeficientes em K [ X ], o anel polinomial ; isto é, funções algébricas implicitamente definidas . Os expoentes r aqui são certos números racionais, dependendo do ramo escolhido; e as soluções em si são séries de potência em
- K[[Y]]
com Y = X 1 / d para um denominador d correspondente ao ramo. O polígono de Newton fornece uma abordagem algorítmica eficaz para calcular d .
Após a introdução dos números p-adic, foi mostrado que o polígono de Newton é tão útil em questões de ramificação para campos locais e, portanto, na teoria algébrica dos números . Os polígonos de Newton também têm sido úteis no estudo de curvas elípticas .
Definição[editar | editar código-fonte]
A priori, dado um polinômio sobre um campo, o comportamento das raízes (supondo que ele tenha raízes) será desconhecido. Os polígonos de Newton fornecem uma técnica para o estudo do comportamento das raízes.
Deixei ser um campo local com avaliação discreta e deixar
com . Então o polígono de Newton é definido como o casco inferior convexo do conjunto de pontos
ignorando os pontos com . Reimplantado geometricamente, plote todos esses pontos P i no plano xy . Vamos supor que os índices de pontos aumentem da esquerda para a direita ( P 0 é o ponto mais à esquerda, P n é o ponto mais à direita). Então, começando em P 0, desenhe um raio diretamente paralelo ao eixo y e gire esse raio no sentido anti-horário até atingir o ponto P k 1 (não necessariamente P 1 ). Quebre o raio aqui. Agora desenhe um segundo raio de P k 1 diretamente paralelo ao eixo y e gire esse raio no sentido anti-horário até atingir o ponto P k 2 . Continue até que o processo atinja o ponto P n ; o polígono resultante (contendo os pontos P 0, P k 1, P k 2 ,. . ., P km, P n ) é o polígono de Newton.
Outra maneira, talvez mais intuitiva, de ver esse processo é essa : Considerar uma faixa de borracha em torno de todos os pontos P 0,. . ., P n . Estique a banda para cima, de modo que ela fique presa no lado inferior por alguns dos pontos (os pontos agem como pregos, parcialmente martelados no plano xy). Os vértices do polígono de Newton são exatamente esses pontos.
Para um diagrama detalhado disso, consulte o Capítulo 6 de "Local Fields", de JWS Cassels, LMS Student Textts 3, CUP 1986. Está na p99 da edição de bolso de 1986.
História[editar | editar código-fonte]
Os polígonos de Newton têm o nome de Isaac Newton, que os descreveu pela primeira vez e alguns de seus usos em correspondência desde o ano de 1676, dirigido a Henry Oldenburg . [1]
Formulários[editar | editar código-fonte]
Às vezes, um polígono de Newton é um caso especial de um ru , e pode ser usado para construir soluções assintóticas de equações polinomiais de duas variáveis, como
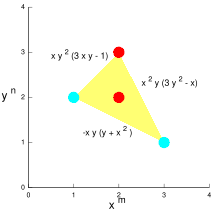
Outra aplicação do polígono de Newton vem do seguinte resultado:
A partir de , suponha que as inclinações dos segmentos de linha do polígono de Newton de (conforme definido acima) organizados em ordem crescente e
sejam os comprimentos correspondentes dos segmentos de linha projetados no eixo x (ou seja, se tivermos um segmento de linha que se estende entre os pontos e então o comprimento é ) Então, para cada número inteiro , tem exatamente raízes com avaliação .
Explicação da função simétrica[editar | editar código-fonte]
No contexto valorativo, recebemos certas informações na forma de valores de funções simétricas elementares das raízes de um polinômio e exigimos informações sobre as avaliações das raízes reais, em um fechamento algébrico . Isso tem aspectos tanto da teoria da ramificação quanto da teoria da singularidade . As inferências válidas possíveis são para avaliações de somas de poder, por meio das identidades de Newton .
Veja também[editar | editar código-fonte]
- Cristal F
- Critério de Eisenstein
- Corpo de Newton-Okounkov
Referências[editar | editar código-fonte]
Referências
- ↑ Egbert Brieskorn, Horst Knörrer (1986). Plane Algebraic Curves, pp. 370–383.
- Goss, David (1996), Basic structures of function field arithmetic, ISBN 978-3-540-61087-8, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 35, Berlin, New York: Springer-Verlag, MR 1423131, doi:10.1007/978-3-642-61480-4 Goss, David (1996), Basic structures of function field arithmetic, ISBN 978-3-540-61087-8, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 35, Berlin, New York: Springer-Verlag, MR 1423131, doi:10.1007/978-3-642-61480-4 Goss, David (1996), Basic structures of function field arithmetic, ISBN 978-3-540-61087-8, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 35, Berlin, New York: Springer-Verlag, MR 1423131, doi:10.1007/978-3-642-61480-4
- Gouvêa, Fernando : números p-adic: uma introdução. Springer Verlag 1993. p. 199
Ligações externas[editar | editar código-fonte]
[[Categoria:Isaac Newton]] [[Categoria:Teoria algébrica dos números]] [[Categoria:!Páginas com traduções não revistas]]




![{\displaystyle f(x)=a_{n}x^{n}+\cdots +a_{1}x+a_{0}\in K[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d652b823c6e4929d4272b63ba4de1f11b164053)













