Bouquet de círculos
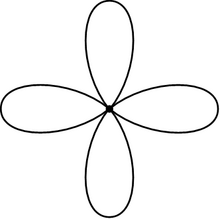
Em matemática, um bouquet de círculos (também conhecido como uma rosa) é um espaço topológico que se obtém ao colar uma coleção de círculos em um ponto. Os círculos da rosa são chamados de pétalas. Bouquets são importantes em topologia algébrica, onde têm relação com os grupos livres.
Definição
[editar | editar código-fonte]
O bouquet é a soma wedge de círculos. Em outras palavras, o bouquet é o espaço quociente C/S, em que C é uma união disjunta de círculos e S um conjunto consistindo de um ponto de cada círculo. Como complexo celular, um bouquet possui um só vértice, e uma aresta para cada círculo. Isso faz dele um grafo topológico.
Uma rosa com n pétalas também pode ser obtida através da identificação de n' pontos de um único cículo. A rosa com duas pétalas é conhecida como figura em figura oito.
Ver também
[editar | editar código-fonte]Referências
[editar | editar código-fonte]- Hatcher, Allen (2002), Algebraic topology, ISBN 0-521-79540-0, Cambridge, UK: Cambridge University Press
- Munkres, James R. (2000), Topology, ISBN 0-13-181629-2, Englewood Cliffs, N.J: Prentice Hall, Inc
- Stillwell, John (1993), Classical topology and combinatorial group theory, ISBN 0-387-97970-0, Berlin: Springer-Verlag
