Grafo de Gray

Grafo de Gray
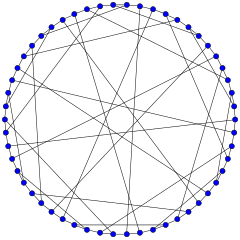	; ; O grafo de Gray
Nomeado em honra a	Marion Cameron Gray
vértices	54
arestas	81
Raio	6
Diâmetro	6
Cintura	8
Automorfismos	1296
Número cromático	2
Índice cromático	3
Propriedades	Cúbico; Hamiltoniano; Semi-simétrico

No campo da matemática da teoria dos grafos o grafo de Gray é um grafo não direcionado bipartido, com 54 vértices e 81 arestas. É um grafo cúbico: todo vértice toca exatamente três arestas. Foi descoberto por Marion C. Gray, em 1932, (de forma inédita), em seguida, descoberto independentemente por Bouwer 1968, em resposta a uma pergunta feita por Jon Folkman em 1967^[1]. O grafo de Gray é interessante como o primeiro exemplo conhecido de um grafo cúbico tendo a propriedade algébrica de ser aresta-transitivo, mas não sendo vértice-transitivo (ver abaixo).

O grafo de Gray tem um número cromático 2, índice cromático 3, raio 6 e diâmetro 6. Ele é também um grafo 3-vértice-conectado e 3-aresta-conectado não-planar.

Construção

O grafo de Gray pode ser construído ^[2] dos 27 pontos de uma grade de 3 × 3 × 3 e as 27 linhas de eixo paralelo a esses pontos. Esta coleção de pontos e linhas formam um configuração projetiva: cada ponto tem exatamente três linhas, através dele, e cada linha tem exatamente três pontos sobre ela. O grafo de Gray é o grafo de Levi dessa configuração, que tem um vértice para cada ponto e para cada linha da configuração, e uma aresta para cada par de um ponto e uma linha que se tocam. Esta construção generaliza (Bouwer 1972) para qualquer dimensão n ≥ 3, rendendo um grafo de Levi n-valente com propriedades algébricas semelhantes às do gráfico deGray.

Em (Monson, Pisanski, Schulte, Ivic-Weiss 2007)^[3], o grafo de Gray aparece como um tipo diferente de grafo de Levi com as arestas e faces triangulares de uma determinada localmente toroidal resumo regular 4 politopo. É, portanto, o primeiro de uma família infinita de grafos cúbicos similarmente construídos.

Marušič e Pisanski (2000)^[4] indicaram vários métodos alternativos de construção do grafo de Gray. Como acontece com qualquer grafo bipartido, não há ciclos de comprimento impar, e também não há ciclos de quatro ou seis vértices, de modo que a cintura do gráfico Gray é 8. A superfície orientada mais simples sobre a qual o grafo de Gray pode ser incorporado tem gênero 7^[5]. O grafo de Gray é hamiltoniano e pode ser construído a partir da notação LCF:

[-25,7,-7,13,-13,25]^{9}.\

Propriedades algébricas

O grupo de automorfismo do grafo de Gray é um grupo de ordem 1296. Ele atua transitivamente nas arestas do grafo, mas não em seus vértices : existem simetrias levando cada aresta para qualquer outra aresta mas não tomando cada vértice para qualquer outro vértice. Os vértices que correspondem a pontos da configuração subjacentes apenas podem ser simétricos para outros vértices que correspondem a pontos, e os vertices que correspondem a linhas só podem ser simétricos para outros vértices que correspondem a linhas. Portanto, o grafo de Gray é um grafo semi-simétrico, o menor possível grafo semi-simétrico cúbico.

O polinômio característico do grafo de Gray é

(x-3)x^{16}(x+3)(x^{2}-6)^{6}(x^{2}-3)^{12}.\

Referências

↑ Folkman, Jon (1967). «Regular line-symmetric graphs». Journal of Combinatorial Theory. 3. p. 533-535. doi:10.1016/S0021-9800(67)80069-3 .
↑ Bouwer, I. Z. (1972). «An edge but not vertex transitive regular graphs». Journal of Combinatorial Theory, Series B. 12. pp. 32–40. doi:10.1016/0095-8956(72)90030-5 .
↑ Monson, B.; Pisanski, T.; Schulte, E.; Ivic-Weiss, A. (2007), «Semisymmetric Graphs from Polytopes», Journal of Combinatorial Theory, Series A, 114: 421–435
↑ v, Dragan; Pisanski, Tomaž (2000). «The Gray graph revisited». Journal of Graph Theory. 35. pp. 1–7. doi:10.1002/1097-0118(200009)35:1<1::AID-JGT1>3.0.CO;2-7 .
↑ Marušič, Dragan; Pisanski, Tomaž; Wilson, Steve (2005). «The genus of the Gray graph is 7». European Journal of Combinatorics. 26 (3–4). p. 377–385. doi:10.1016/j.ejc.2004.01.015 .