Lista de distribuições de probabilidade

Muitas distribuições de probabilidade, que são importantes na teoria ou aplicações, receberam nomes específicos.

Distribuições discretas

Com suporte finito 

distribuição uniforme discreta

• A distribuição uniforme discreta, onde todos os elementos de um finito definido são igualmente prováveis. Este é o modelo teórico da distribuição de uma moeda equilibrada, um dado justo, uma roleta de cassino, ou a primeira carta de um baralho bem embaralhado.

Intervalo de valores dos parâmetros:	$n\in \mathbb {N}$, $k_{i}\in \mathbb {R} \;(i=1,\dots ,n)$	Imagem da função de probabilidade: onde $\{1,2,\dots ,20\}$, d. q. $n=20$
suporte:	$\{k_{i}:i=1,\dots ,n\}$
densidade discreta:	$f(k)={\frac {1}{n}}$
função de distribuição:	$P(\{X\leq x\})={\frac {|\{i:k_{i}\leq x\}|}{n}}$
	$P(\{X<x\})={\frac {|\{i:k_{i}<x\}|}{n}}$
valor esperado:	${\frac {1}{n}}\sum _{i=1}^{n}k_{i}$
variância:	${\frac {1}{n}}\left(\sum _{i=1}^{n}k_{i}^{2}-{\frac {1}{n}}\left(\sum _{i=1}^{n}k_{i}\right)^{2}\right)$

Distribuição de Bernoulli

• Distribuição de Bernoulli, que toma o valor 1 com probabilidade p e o valor 0 com probabilidade q = 1 − p.

Intervalo de valores dos parâmetros:	$p\in [0,1]$	Imagem da função de probabilidade: $p=0{,}2$ (azul), $p=0{,}5$ (verde) und $p=0{,}8$ (vermelho)
suporte:	$\{0,1\}$
densidade discreta:	$f(k)={\begin{cases}p&{\text{se }}k=1\\1-p&{\text{se }}k=0\end{cases}}$
função de distribuição:	$P(\{X\leq x\})={\begin{cases}0&{\text{se }}x<0\\1-p&{\text{se }}0\leq x<1\\1&{\text{se }}x\geq 1\end{cases}}$
	$P(\{X<x\})={\begin{cases}0&{\text{se }}x\leq 0\\1-p&{\text{se }}0<x\leq 1\\1&{\text{se }}x>1\end{cases}}$
valor esperado:	$p$
variância:	$p(1-p)$

Distribuição binomial

• Distribuição binomial, que descreve o número de sucessos em uma série de experimentos Sim/Não independente, todos com a mesma probabilidade de sucesso.

Intervalo de valores dos parâmetros:	$n\in \mathbb {N} ^{+}$, $p\in [0,1]$	Imagem da função de probabilidade: $n=20$; $p=0{,}1$ (azul), $p=0{,}5$ (verde) und $p=0{,}8$ (vermelho)
suporte:	$\{0,1,\dots ,n\}$
densidade discreta:	$f(k)={n \choose k}p^{k}(1-p)^{n-k}$
função de distribuição:	$P(\{X\leq x\})=\sum _{i=0}^{\lfloor x\rfloor }{\binom {n}{i}}p^{i}(1-p)^{n-i}$
	$P(\{X<x\})=\sum _{i=0}^{\lceil x-1\rceil }{n \choose i}p^{i}(1-p)^{n-i}$
valor esperado:	$np$
variância:	$np(1-p)$

Distribuição geométrica

Variante A

Intervalo de valores dos parâmetros:	$p\in ]0,1[$	Imagem da função de probabilidade: $p=0{,}2$ (azul), $p=0{,}5$ (verde) und $p=0{,}8$ (vermelho)
suporte:	$\mathbb {N} ^{+}$
densidade discreta:	$f(k)=p(1-p)^{k-1}$
função de distribuição:	$P(\{X\leq x\})=1-(1-p)^{\lfloor x\rfloor }$
	$P(\{X<x\})=1-(1-p)^{\lceil x-1\rceil }$
valor esperado:	${\frac {1}{p}}$
variância:	${\frac {1}{p^{2}}}-{\frac {1}{p}}$

Variante B

Intervalo de valores dos parâmetros:	$p\in ]0,1[$	Imagem da função de probabilidade: $p=0{,}2$ (azul), $p=0{,}5$ (verde) und $p=0{,}8$ (vermelho)
suporte:	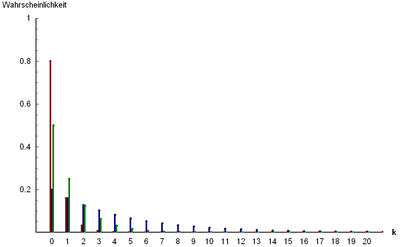$\mathbb {N} _{0}$
densidade discreta:	$f(k)=p(1-p)^{k}$
função de distribuição:	$P(\{X\leq x\})=1-(1-p)^{\lfloor x+1\rfloor }$
	$P(\{X<x\})=1-(1-p)^{\lceil x\rceil }$
valor esperado:	${\frac {1}{p}}-1$
variância:	${\frac {1}{p^{2}}}-{\frac {1}{p}}$

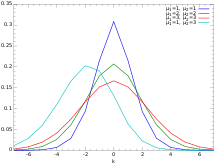
Distribuição hipergeométrica

• Distribuição hipergeométrica, que descreve o número de sucessos no primeiro m de uma série de n experimentos Sim/Não consecutivos, se o número total de sucessos é conhecido. Esta distribuição surge quando não há substituição.

Intervalo de valores dos parâmetros:	$N\in \mathbb {N} ^{+}$, $M\in \mathbb {N} ^{+}$ com $M\leq N$, $n\in \mathbb {N} ^{+}$ com $n\leq N$	Imagem da função de probabilidade: $n=20$; $M=20,N=30$ (azul), $M=50,N=60$ (verde) e $M=20,N=60$ (vermelho)
suporte:	$\{\max(0,n+M-N),\dotsc ,\min(n,M)\}$
densidade discreta:	$f(k)={\frac {\displaystyle {M \choose k}{N-M \choose n-k}}{\displaystyle {N \choose n}}}$
função de distribuição:	$P(\{X\leq x\})=\sum _{i=\max(0,n-N)}^{\lfloor x\rfloor }{\frac {{M \choose i}{N \choose n-i}}{M+N \choose n}}$
	$P(\{X<x\})=\sum _{i=\max(0,n-N)}^{\lceil x-1\rceil }{\frac {{M \choose i}{N \choose n-i}}{M+N \choose n}}$
valor esperado:	$n{\frac {M}{N}}$
variância:	$n{\frac {M}{N}}\left(1-{\frac {M}{N}}\right){\frac {N-n}{N-1}}$

• Distribuição de Rademacher, que toma o valor 1 com probabilidade 1/2 e valor −1 com probabilidade 1/2.
• Distribuição beta-binomial, que descreve o número de sucessos em uma série independente de Sim/Não, com experimentos com a heterogeneidade da probabilidade de sucesso.
• Distribuição degenerada em x₀, onde X é determinado o valor de x₀. Isso não parece aleatório, mas ele satisfaz a definição de variável aleatória. Isso é útil porque põe determinista variáveis e variáveis aleatórias no mesmo formalismo.

• Distribuição binomial Poisson , que descreve o número de sucessos em uma série de experimentos Sim/Não independente com diferentes probabilidades de sucesso.
• Distribuição hipergeométrica não-central de Fisher
• Distribuição hipergeométrica não-central de Wallenius
• Lei de Benford, que descreve a frequência do primeiro dígito de muitos que ocorrem naturalmente dados.

Distribuição Binomial

Distribuição degenerada

Distribuição de Poisson

Distribuição Skellam

Com suporte infinito

distribuição binomial negativa

• distribuição binomial negativa ou Pascal de distribuição de uma generalização da distribuição geométrica para a nth o sucesso.

Intervalo de valores dos parâmetros:	$r\in \mathbb {N} ^{+}$, $p\in ]0,1]$	Imagem da função de probabilidade: $r=10$; $p=0{,}2$ (azul), $p=0{,}5$ (verde) und $p=0{,}8$ (vermelho)
suporte:	$\{x\in \mathbb {N} \colon x\geq r\}$
densidade discreta:	$P(\{X=k\})={{k-1} \choose {r-1}}p^{r}(1-p)^{k-r}$
função de distribuição:	$P(\{X\leq x\})=\sum _{i=r}^{\lfloor x\rfloor }{i-1 \choose r-1}p^{r}(1-p)^{i-r}$
	$P(\{X<x\})=\sum _{i=r}^{\lceil x-1\rceil }{i-1 \choose r-1}p^{r}(1-p)^{i-r}$
valor esperado:	${\frac {r}{p}}$
variância:	${\frac {r(1-p)}{p^{2}}}$

distribuição de Poisson

• A distribuição de Poisson, que descreve um número muito grande de individualmente eventos improváveis que acontecem em um determinado intervalo de tempo. Relacionados a esta distribuição são uma série de outras distribuições: os deslocados de Poisson, o hyper-Poisson, em geral Poisson, binomial e Poisson tipo de distribuições.

Intervalo de valores dos parâmetros:	$\lambda \in \mathbb {R} ^{+}$	Imagem da função de probabilidade: $\lambda =1$ (azul), $\lambda =5$ (verde) e $\lambda =10$ (vermelho)
suporte:	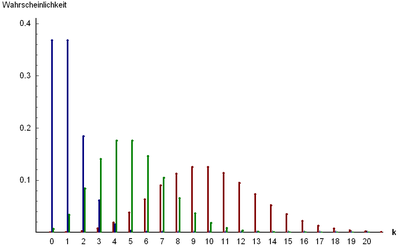$\mathbb {N} _{0}$
densidade discreta:	$f(k)={\frac {\lambda ^{k}}{k!}}\cdot \mathrm {e} ^{-\lambda }$
função de distribuição:	$P(\{X\leq x\})=\sum _{i=0}^{\lfloor x\rfloor }{\frac {\lambda ^{i}}{i!}}\;\mathrm {e} ^{-\lambda }$
	$P(\{X<x\})=\sum _{i=0}^{\lceil x-1\rceil }{\frac {\lambda ^{i}}{i!}}\;\mathrm {e} ^{-\lambda }$
valor esperado:	$\lambda$
variância:	$\lambda$

• • Distribuição Conway–Maxwell–Poisson de, um parâmetro de extensão da distribuição de Poisson com uma taxa ajustável de decadência.
  • distribuição Poisson truncada em Zero, para processos em que zero contagens não são observados.
• Distribuição composto de Poisson discreto
• Distribuição beta binomial negativa

Distribuição logarítmica (série)

• Distribuição logarítmica (série) 

Intervalo de valores dos parâmetros:	$p\in (0,1)$	Imagem da função de probabilidade: $p=0{,}2$ (azul), $p=0{,}5$ (verde) und $p=0{,}8$ (vermelho)
suporte:	$\mathbb {N} ^{+}$
densidade discreta:	$f(k)={\frac {p^{k}}{k}}\cdot {\frac {1}{-\ln(1-p)}}$
função de distribuição:	$P(\{X\leq x\})=\sum _{i=0}^{\lfloor x\rfloor }{\frac {p^{i}}{i}}\cdot {\frac {1}{-\ln(1-p)}}$
	$P(\{X<x\})=\sum _{i=0}^{\lceil x-1\rceil }{\frac {p^{i}}{i}}\cdot {\frac {1}{-\ln(1-p)}}$
valor esperado:	${\frac {p}{-(1-p)\ln(1-p)}}$
variância:	${\frac {p(-\ln(1-p)-p)}{(1-p)^{2}\ln ^{2}(1-p)}}$

• A distribuição de Boltzmann, uma distribuição discreta importante na física estatística, que descreve as probabilidades das várias discretos níveis de energia de um sistema em equilíbrio térmico. Ele tem um contínuo analógico. Casos especiais incluem:
  • Distribuição de Boltzmann
  • Distribuição de Maxwell-Boltzmann
• Distribuição Borel
• Distribuição Champernowne
• Distribuição binomial negativa estendida
• Distribuição hipergeométrica estendida
• distribuição log-série generalizada
• Distribuição geométrica, uma distribuição discreta que descreve o número de tentativas necessárias para obter o primeiro sucesso em uma série de tentativas de Bernoulli independentes, ou, alternativamente, apenas o número de perdas antes do primeiro sucesso (i.e. um a menos).

• Distribuição parabólico fractal 

• Distribuição de Polya–Eggenberger
• Distribuição Skellam, a distribuição da diferença entre duas variáveis aleatórias com distribuídos de Poisson independentes.
• Distribuição elíptica inclinada
• Distribuição Yule–Simon
• distribuição zeta tem usos em estatística aplicada e mecânica estatística e pode ser de interesse para o número de teóricos. É a distribuição Zipf para um número infinito de elementos.
• A lei de Zipf ou a distribuição Zipf. Uma discreta da lei de potência de distribuição, o exemplo mais famoso dos quais é a descrição da frequência de ocorrência de palavras no idioma inglês.
• A lei Zipf-Mandelbrot é uma distribuição discreta de lei de poder, que é uma generalização da distribuição Zipf.

Distribuições contínuas

Distribuição Beta

Contínua distribuição uniforme

Com suporte em um intervalo limitado

• O arco-seno de distribuição em [a,b], que é um caso especial da distribuição Beta se a = 0 e b = 1.
• A distribuição Beta em [0,1], uma família de dois parâmetros de distribuições com um modo, de que a distribuição uniforme é um caso especial, e que é útil na estimativa de probabilidades de sucesso.
• O logitnormal de distribuição em (0,1).
• A função delta de Dirac embora não seja estritamente uma função, é uma limitação formulário de muitos de probabilidade contínua funções. Ele representa uma discreta distribuição de probabilidade concentrada em 0 — um degenerado de distribuição — , mas a notação trata como se fosse uma distribuição contínua.
• A contínua distribuição uniforme ou retangular de distribuição em [a,b], onde todos os pontos em um intervalo finito são igualmente prováveis.
• A Irwin–Hall de distribuição é a distribuição da soma de n eu.eu.d. U(0,1) variáveis aleatórias.
• O Bates distribuição é a distribuição da média de n eu.eu.d. U(0,1) variáveis aleatórias.
• O Kent distribuição sobre as três dimensões da esfera.
• O Kumaraswamy de distribuição é tão versátil como a distribuição Beta, mas simples formas fechadas, tanto para o fcd e o pdf.
• A distribuição logarítmica (contínua)
• O Marchenko–Pastur de distribuição é importante na teoria de matrizes aleatórias.
• A distribuição PERT é um caso especial da distribuição beta
• O cosseno levantado distribuição [${\displaystyle }$]
• A recíproca distribuição
• A distribuição triangular em [a, b], um caso especial de que é a distribuição da soma de dois independentes distribuídos uniformemente variáveis aleatórias (a convolução de duas distribuições uniforme).
• A distribuição trapezoidal
• A distribuição normal truncada em [a, b].
• O U-quadrática de distribuição em [a, b].
• O von Mises-Fisher distribuição no N-dimensional esfera tem o von Mises distribuição como um caso especial.
• O Wigner semicírculo de distribuição é importante na teoria de matrizes aleatórias.

Distribuição Chi-squared

Distribuição gama

Distribuição de Pareto

Com suporte em intervalos de comprimento de 2ππ – direcional distribuições

• O von Mises distribuição
• O envolto distribuição normal
• O envolto distribuição exponencial
• O envolto Lévy distribuição
• O envolto de Cauchy de distribuição
• O envolto de Laplace de distribuição
• O envolto assimétrica distribuição de Laplace
• O pente de Dirac de período 2 π embora não seja estritamente uma função, é uma limitação formulário de muitos direcional distribuições. É, essencialmente, um embrulho de função delta de Dirac. Ele representa uma discreta distribuição de probabilidade concentrada em 2πn — um degenerado de distribuição — , mas a notação trata como se fosse uma distribuição contínua.

Apoiada sobre semi-infinitos intervalos, geralmente [0,∞)

• The Beta prime distribution
• The Birnbaum–Saunders distribution, also known as the fatigue life distribution, is a probability distribution used extensively in reliability applications to model failure times.
• The chi distribution
  • The noncentral chi distribution
• The chi-squared distribution, which is the sum of the squares of n independent Gaussian random variables. It is a special case of the Gamma distribution, and it is used in goodness-of-fit tests in statistics.
  • The inverse-chi-squared distribution
  • The noncentral chi-squared distribution
  • The Scaled-inverse-chi-squared distribution
• The Dagum distribution
• The exponential distribution, which describes the time between consecutive rare random events in a process with no memory.
• The Exponential-logarithmic distribution
• The F-distribution, which is the distribution of the ratio of two (normalized) chi-squared-distributed random variables, used in the analysis of variance. It is referred to as the beta prime distribution when it is the ratio of two chi-squared variates which are not normalized by dividing them by their numbers of degrees of freedom.
  • The noncentral F-distribution
• Fisher's z-distribution
• The folded normal distribution
• The Fréchet distribution
• The Gamma distribution, which describes the time until n consecutive rare random events occur in a process with no memory.
  • The Erlang distribution, which is a special case of the gamma distribution with integral shape parameter, developed to predict waiting times in queuing systems
  • The inverse-gamma distribution
• The Generalized gamma distribution
• The generalized Pareto distribution
• The Gamma/Gompertz distribution
• The Gompertz distribution
• The half-normal distribution
• Hotelling's T-squared distribution
• The inverse Gaussian distribution, also known as the Wald distribution
• The Lévy distribution
• The log-Cauchy distribution
• The log-Laplace distribution
• The log-logistic distribution
• The log-normal distribution, describing variables which can be modelled as the product of many small independent positive variables.
• The Lomax distribution
• The Mittag-Leffler distribution
• The Nakagami distribution
• The Pareto distribution, or "power law" distribution, used in the analysis of financial data and critical behavior.
• The Pearson Type III distribution
• The Phase-type distribution, used in queueing theory
• The phased bi-exponential distribution is commonly used in pharmokinetics
• The phased bi-Weibull distribution
• The Rayleigh distribution
• The Rayleigh mixture distribution
• The Rice distribution
• The shifted Gompertz distribution
• The type-2 Gumbel distribution
• The Weibull distribution or Rosin Rammler distribution, of which the exponential distribution is a special case, is used to model the lifetime of technical devices and is used to describe the particle size distribution of particles generated by grinding, milling and crushing operations.

Distribuição de Cauchy

Distribuição Laplace

Distribuição estável

Suporte em toda a linha real

• The Behrens–Fisher distribution, which arises in the Behrens–Fisher problem.
• The Cauchy distribution, an example of a distribution which does not have an expected value or a variance. In physics it is usually called a Lorentzian profile, and is associated with many processes, including resonance energy distribution, impact and natural spectral line broadening and quadratic stark line broadening.
• Chernoff's distribution
• The Exponentially modified Gaussian distribution, a convolution of a normal distribution with an exponential distribution.
• The Fisher–Tippett, extreme value, or log-Weibull distribution
• Fisher's z-distribution
• The skewed generalized t distribution
• The generalized logistic distribution
• The generalized normal distribution
• The geometric stable distribution
• The Gumbel distribution
• The Holtsmark distribution, an example of a distribution that has a finite expected value but infinite variance.
• The hyperbolic distribution
• The hyperbolic secant distribution
• The Johnson SU distribution
• The Landau distribution
• The Laplace distribution
• The Lévy skew alpha-stable distribution or stable distribution is a family of distributions often used to characterize financial data and critical behavior; the Cauchy distribution, Holtsmark distribution, Landau distribution, Lévy distribution and normal distribution are special cases.
• The Linnik distribution
• The logistic distribution
• The map-Airy distribution
• The normal distribution, also called the Gaussian or the bell curve. It is ubiquitous in nature and statistics due to the central limit theorem: every variable that can be modelled as a sum of many small independent, identically distributed variables with finite mean and variance is approximately normal.
• The Normal-exponential-gamma distribution
• The Normal-inverse Gaussian distribution
• The Pearson Type IV distribution (see Pearson distributions)
• The skew normal distribution
• Student's t-distribution, useful for estimating unknown means of Gaussian populations.
  • The noncentral t-distribution
  • The skew t distribution
• The type-1 Gumbel distribution
• The Tracy–Widom distribution
• The Voigt distribution, or Voigt profile, is the convolution of a normal distribution and a Cauchy distribution. It is found in spectroscopy when spectral line profiles are broadened by a mixture of Lorentzian and Doppler broadening mechanisms.
• The Gaussian minus exponential distribution is a convolution of a normal distribution with (minus) an exponential distribution.
• The Chen distribution.

Com a variável suporte

• A generalizada do valor extremo de distribuição tem um limite superior finito ou um finito limite inferior, dependendo do que alcance o valor de um dos parâmetros da distribuição está (ou é suportada em toda a linha real para um valor especial do parâmetro
• O generalizada de Pareto distribuição tem um suporte que é delimitada abaixo, ou limitado acima e abaixo
• A Tukey lambda de distribuição é suportado em toda a linha real, ou em um intervalo limitado, dependendo de qual intervalo o valor de um dos parâmetros da distribuição.
• O Wakeby de distribuição

Misto discreto/contínuo distribuições

• A rectificado distribuição Gaussiana substitui valores negativos a partir de uma distribuição normal com um componente discreto do zero.
• O composto de poisson-gama ou Tweedie distribuição é contínua sobre o estritamente positivo números reais, com uma missa em zero.

Distribuições conjunta

Para qualquer conjunto de independentes, variáveis aleatórias a função de densidade de probabilidade de sua distribuição conjunta é o produto das suas funções de densidade.

Duas ou mais variáveis aleatórias no mesmo exemplo de espaço

• A distribuição de Dirichlet, uma generalização da distribuição beta.
• O Ewens da amostragem fórmula é uma distribuição de probabilidade sobre o conjunto de todas as partições de um inteiro n, decorrente de genética de populações.
• A Calvície–Nichols modelo
• A distribuição multinomial, uma generalização da distribuição binomial.
• O multivariada distribuição normal, uma generalização da distribuição normal.
• O multivariada distribuição t, uma generalização do t de Student distribuição.
• A negativa de distribuição multinomial, uma generalização da distribuição binomial negativa.
• A generalizada multivariada log-distribuição gama

Matriz com valor de distribuições

• A distribuição.
• O inverso de distribuição.
• A matriz de distribuição normal
• A matriz de t-distribuição

Distribuições não-numéricos 

• Distribuição categórica

Diversas distribuições

• O Cantor de distribuição
• A generalizada logística de distribuição família
• A Pearson distribuição família
• A fase tipo de distribuição

Ver também

• Mistura de distribuição
• Função de distribuição cumulativa
• Probabilidade de função
• A lista de estatísticas tópicos
• Função de densidade de probabilidade
• Variável aleatória
• Histograma
• Truncado distribuição
• De cópula (estatísticas)
• Distribuição de probabilidade
• Relações entre distribuições de probabilidade
• ProbOnto uma base de conhecimento e a ontologia de distribuições de probabilidade, URL: probonto.org