Teorema de Ptolomeu

O teorema de Ptolomeu refere-se a qualquer quadrilátero inscritível por uma circunferência, e pode ser enunciado da seguinte forma:

"O produto das diagonais é igual a soma dos produtos dos lados opostos". Isto é, sendo m e n suas diagonais, a,b,c e d seus lados, vale que: $m\cdot n=a\cdot c+b\cdot d$. Este teorema pode ser demonstrado da seguinte maneira:

Ilustração do teorema

Construção do teorema.

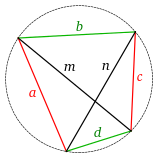
Seja, como na figura ao lado, um quadrilátero ABCD inscrito numa circunferência de centro O. Vamos provar que $AC.BD=AB.CD+AD.BC$, isto é, provar que o produto das diagonais é igual a soma dos produtos dos lados opostos. Para isso, a partir do vértice A traçamos uma semirreta que intersecciona a semirreta ${\overrightarrow {CD}}$ num ponto P tal que$m\angle {BAC}=m\angle {DAP}$. Dado que o quadrilátero ABCD é inscritível, podemos dizer que seus ângulos opostos são suplementares ( ver [1]). Assim, é verdade que $\angle {ABC}$ é suplementar a $\angle {ADC}$. Da mesma maneira, temos que $\angle {ADP}$ é suplementar a $\angle {ADC}$, o que segue daí que são iguais: $m\angle {ABC}=m\angle {ADP}$. Assim, observe então que os triângulos BAC e DAP têm dois ângulos congruentes e podemos concluir que estes são semelhantes entre si pelo caso ângulo-ângulo (ver [2]). Disto é válido dizer que ${\frac {AB}{AD}}={\frac {BC}{DP}}$, que é o mesmo que $DP={\frac {(AD)(BC)}{AB}}$. Como construímos que $m\angle {BAD}=m\angle {CAP}$, segue que $m\angle {BAD}=m\angle {CAP}$e, da semelhança de triângulos que acabamos de mostrar, que ${\frac {AB}{AD}}={\frac {AC}{AP}}$. Então, pelo caso lado-ângulo-lado de semelhança de triângulos (ver [3]), dizemos que os triângulos ABD e ACP são semelhantes. Por conseguinte, também podemos inferir disso que ${\frac {BD}{CP}}={\frac {AB}{AC}}$, que é o mesmo que $CP={\frac {(AC)(BD)}{AB}}$. Mas perceba pela figura ao lado que $CP=CD+DP$. Substituindo tudo que já encontramos nessa expressão, teremos que ${\frac {(AC)(BD)}{AB}}=CD+{\frac {(AD)(BC)}{AB}}$. Resolvendo a expressão, podemos concluir então que$AC.BD=AB.CD+AD.BC$, como queríamos.