Teste de normalidade
Em estatística, os testes de normalidade são usados para determinar se um conjunto de dados de uma dada variável aleatória, é bem modelada por uma distribuição normal ou não, ou para calcular a probabilidade da variável aleatória subjacente estar normalmente distribuída.
Mais precisamente, os testes são uma forma de selecção de modelos, e podem ser interpretados de várias maneiras, dependendo de como cada um interpreta as probabilidades:
Exemplos de aplicações
[editar | editar código-fonte]- Testar a normalidade dos resíduos de uma regressão linear. A regressão linear só deve ser usada se os erros são normais, portanto, caso o teste aponte que esta premissa é inválida, os resultados da regressão (intervalos de confiança, etc) não podem ser usados. Neste caso, o modelo deve ser modificado (introduzindo outras variáveis explanatórias, ou mudando o modelo) para que os erros se comportem como uma variável normal
Métodos empíricos e gráficos
[editar | editar código-fonte]Histograma da distribuição
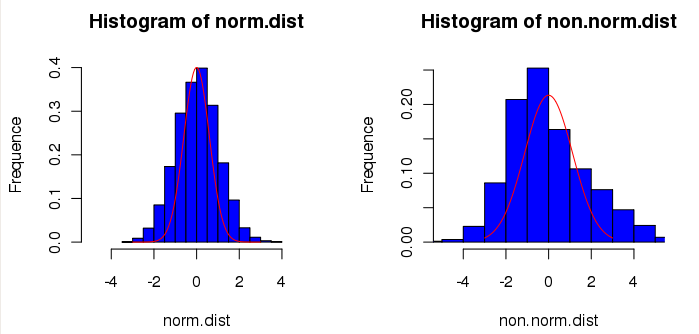
[editar | editar código-fonte]É possível visualizar a forma da distribuição através do seu histograma, e comparar este histograma com a função densidade de probabilidade da distribuição normal (de mesma média e desvio padrão), ou de qualquer outra distribuição.
Este método simples e rápido pode dar informações (empíricas) sobre a distribuição, por exemplo, uma distribuição com caudas pesadas pode ser melhor modelada por uma t de Student ou mesmo uma distribuição de Cauchy, ou, se for assimétrica, por uma log-normal, Weibull, exponencial ou beta.
Referências
- ↑ Judge et al. (1988) and Gujarati (2003) recommend the Jarque-Bera test.
Referências
[editar | editar código-fonte]- Judge et al, Introduction to the Theory and Practice of Econometrics, Second Edition, 1988; 890-892.
- Gujarati, Damodar N., Basic Econometrics, Fourth Edition, 2003; 147-148
