Transcendentes de Painlevé
Aspeto
Este artigo não cita fontes confiáveis. (Agosto de 2021) |
Em matemática, transcendentes de Painlevé são as soluções para certas equações diferenciais ordinárias de segunda ordem não lineares no plano complexo com a propriedade de Painlevé (as únicas singularidades móveis são polos), mas que geralmente não são solucionáveis em termos de funções elementares. Elas foram descobertas por Paul Painlevé (1900 - 1902), que mais tarde tornou-se o primeiro-ministro francês.
Listas de equações de Painlevé
[editar | editar código-fonte]Estas seis equações, tradicionalmente chamadas Painlevé I-VI, são as seguintes:
- I (Painlevé):
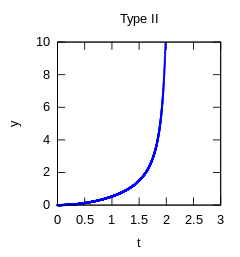
- II (Painlevé):
- III (Painlevé):
- IV (Gambier):
- V (Gambier):
- VI (R. Fuchs):
Os números α, β, γ, δ são constantes complexas.
Referências
- Painlevé Transcendents - MathWorld