Usuário(a):MGromov/Testes27

O modelo de Morris–Lecar é um modelo de disparos neuronais desenvolvido por Catherine Morris e Harold Lecar para reproduzir a variedade de comportamentos de oscilação associada à condutância de Ca⁺⁺ e K⁺ na fibra muscular do ''Balanus nubilus''.^[1] Os neurônios de Morris–Lecar caracterizam-se por possuir tanto a classe I quanto a classe II de excitação neuronal.

História[editar | editar código-fonte]

Catherine Morris (nascida em 24 de dezembro de 1949) é uma bióloga canadense. Recebeu uma bolsa da Commonwealth para estudar na Universidade de Cambridge, onde se tornou doutora em 1977. Assumiu um cargo de professora na Universidade de Ottawa no início dos anos 1980. Desde 2015, é uma professora emérita dessa instituição.

Harold Lecar (18 de outubro de 1935-4 de fevereiro de 2014) foi um professor norte-americano de biofísica e neurobiologia na Universidade da Califórnia, em Berkeley. Doutorou-se em física na Universidade Columbia, em 1963.

Método experimental[editar | editar código-fonte]

Os experimentos de Morris–Lecar basearam-se no método de garra de corrente desenvolvido por Keynes et al., em 1973.^[2]

“

Grandes espécimes da cirripedia Balanus nubilus (Pacific Bio-Marine Laboratories Inc., Venice, Califórnia) foram usados. A cirripedia foi cortada em lâminas laterais, os músculos depressores "scutorum rostralis" foram claramente sinalizados. As fibras individuais foram dissecadas, a partir de uma incisão do tendão. O outro lado do músculo foi cortado próximo a sua ligação à concha e ligado. Fibras isoladas foram ou usadas imediatamente ou mantidas água do mar artificial por trinta minutos antes do uso. Experimentos foram realizados numa sala com tempertatura a 22 C.^[1]

”

Principais pressupostos do modelo de Morris–Lecar[editar | editar código-fonte]

As equações aplicam-se a combinações espacialmente iso-potenciais de membrana. Há duas correntes dependentes de voltagem persistentes (não-inativas) com potenciais reversos com vieses opostos. A corrente de despolarização é levada pelos íon Na+ ou Ca2+ (ou ambos), dependendo do sistema a ser modelado, e a corrente hiperpolarizadora é levada por K+.
Os canais de ativação acompanham mudanças no potencial de membrana de modo suficientemente rápido para que a condutância que é ativada pode voltar instantaneamente a seu estado de repouso sob qualquer voltagem.
A dinâmica da variável de recuperação pode ser aproximada por uma equação diferencial linear de primeira ordem para a probabilidade do canal abrir.^[3]

Descrição fisiológica[editar | editar código-fonte]

O modelo de Morris–Lecar é um sistema bidimensional de equações diferenciais não lineares. É considerado um modelo simples em comparação com o modelo de Hodgkin-Huxley, de quatro dimensões.

Qualitativamente, esse sistema de equações descreve a relação complexa entre o potencial de membrana e ativação de canais de iônicos na membrana: o potencial depende da atividade dos canais iônicos e a atividade dos canais iônicos depende da voltagem. À medida que parâmetros de bifurcação são alterados, diferentes classes de comportamento neuronal são percebidas. $τ N$ está associado à escalas de tempo relativo das dinâmicas de disparo, que varia de maneira geral de célula a célula e tem uma dependência à temperatura significativa.^[3]

Quantitativamente:

{\begin{aligned}C{\frac {dV}{dt}}&~=~I-g_{\mathrm {L} }(V-V_{\mathrm {L} })-g_{\mathrm {Ca} }M_{\mathrm {ss} }(V-V_{\mathrm {Ca} })-g_{\mathrm {K} }N(V-V_{\mathrm {K} })\\{\frac {dN}{dt}}&~=~{\frac {N_{\mathrm {ss} }-N}{\tau _{N}}}\end{aligned}}

onde

{\begin{aligned}M_{\mathrm {ss} }&~=~{\tfrac {1}{2}}\cdot (1+\tanh[{\tfrac {V-V_{1}}{V_{2}}}])\\N_{\mathrm {ss} }&~=~{\tfrac {1}{2}}\cdot (1+\tanh[{\tfrac {V-V_{3}}{V_{4}}}])\\\tau _{N}&~=~1/(\phi \cosh[{\tfrac {V-V_{3}}{2V_{4}}}])\end{aligned}}

Note-se que as equações $M ss$ e $N ss$ podem também ser expressas como $M ss = (1 + Exp[-2(V - V 1) / V 2]) -1$ and $N ss = (1 + Exp[-2(V - V 3) / V 4]) -1$ , mas a maioria dos autores prefere a forma que usa funções hiperbólicas.

Variáveis[editar | editar código-fonte]

$V$ : potencial de membrana
$N$ : variável de recuperação: a probabilidade que o canal K+ esteja conduzindo

Parâmetros e constantes[editar | editar código-fonte]

$I$ : corrente aplicada
$C$ : capacidade de membrana
$g L$ , $g Ca$ , $g K$ : vazamento, condutâncias Ca⁺⁺ e K⁺ por canais de membranas
$V L$ , $V Ca$ , $V K$ : potencial de equilíbrio de canais iônicos relevantes
$V 1$ , $V 2$ , $V 3$ , $V 4$ : parâmetros de equilíbrio para estados de repouso e tempo constante parameters for steady state and time constant
$φ$ : frequência de referência

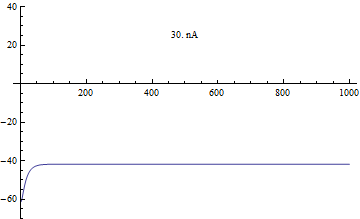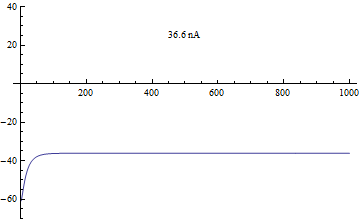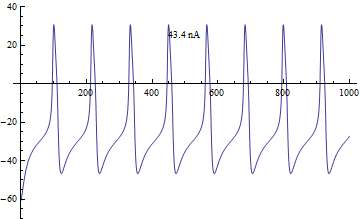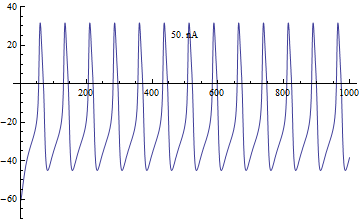
Bifurcações[editar | editar código-fonte]

A bifurcação no modelo de Morris–Lecar foi analisada a partir da corrente aplicada $I$ , como o principal parâmetro de bifurcação, e $φ$ , $g Ca$ , $V 3$ , $V 4$ como os parâmetros secundários para a análise do plano de fase.^[4]

Bifurcações possíveis

Bifurcação de Hopf

Bifurcação SNIC

Bifurcação homoclínica

Simulações de garra de corrente do modelo de Morris–Lecar. A corrente injetada para a bifurcação SNIC e a bifurcação homoclínica varia de 30 nA a 50 nA, enquanto a corrente para a bifurcação de Hopf varia de 80nA a 100nA.

Ver também[editar | editar código-fonte]

Referências

↑ ^a ^b Morris, Catherine; Lecar, Harold (July 1981), «Voltage Oscillations in the barnacle giant muscle fiber», Biophys J., 35 (1): 193–213, PMC 1327511, PMID 7260316, doi:10.1016/S0006-3495(81)84782-0 Verifique data em: |data= (ajuda)
↑ Keynes, RD; Rojas, E; Taylor, RE; Vergara, J (March 1973), «Calcium and potassium systems of a giant barnacle muscle fibre under membrane potential control», The Journal of Physiology (London), 229: 409–455, PMC 1350315, PMID 4724831 Verifique data em: |data= (ajuda)
↑ ^a ^b This assumption is never exactly true, since channel proteins are composed of subunits, which must act in concert, to reach the open state. Despite missing delays in the onset of recovery, the model appears to be adequate for phase-plane considerations for many excitable systems.Lecar, Harold (2007), «Morris-Lecar model», Scholarpedia, 2 (10), doi:10.4249/scholarpedia.1333
↑ Tsumoto, Kunichika; Kitajimab, Hiroyuki; Yoshinagac, Tetsuya; Aiharad, Kazuyuki; Kawakamif, Hiroshi (January 2006), «Bifurcations in Morris–Lecar neuron model» (PDF), Neurocomputing (em English e Japanese), 69 (4–6): 293–316, doi:10.1016/j.neucom.2005.03.006 Verifique data em: |data= (ajuda)

Links externos[editar | editar código-fonte]

Categoria:Neurociência

[ml81-1] Morris, Catherine; Lecar, Harold (July 1981), «Voltage Oscillations in the barnacle giant muscle fiber», Biophys J., 35 (1): 193–213, PMC 1327511, PMID 7260316, doi:10.1016/S0006-3495(81)84782-0 Verifique data em: |data= (ajuda)

[2] Keynes, RD; Rojas, E; Taylor, RE; Vergara, J (March 1973), «Calcium and potassium systems of a giant barnacle muscle fibre under membrane potential control», The Journal of Physiology (London), 229: 409–455, PMC 1350315, PMID 4724831 Verifique data em: |data= (ajuda)

[scholar-3] This assumption is never exactly true, since channel proteins are composed of subunits, which must act in concert, to reach the open state. Despite missing delays in the onset of recovery, the model appears to be adequate for phase-plane considerations for many excitable systems.Lecar, Harold (2007), «Morris-Lecar model», Scholarpedia, 2 (10), doi:10.4249/scholarpedia.1333

[4] Tsumoto, Kunichika; Kitajimab, Hiroyuki; Yoshinagac, Tetsuya; Aiharad, Kazuyuki; Kawakamif, Hiroshi (January 2006), «Bifurcations in Morris–Lecar neuron model» (PDF), Neurocomputing (em English e Japanese), 69 (4–6): 293–316, doi:10.1016/j.neucom.2005.03.006 Verifique data em: |data= (ajuda)

[1]

[2]

[3]

[4]